吴恩达机器学习102：支持向量机最大间距分类器

1.下面是支持向量机(SVM)的代价函数：

　　

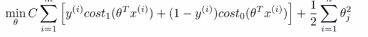
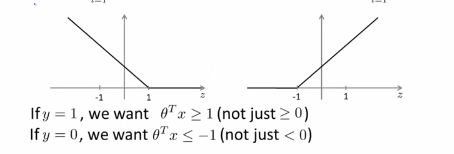
　　上图左边是cost1(z)函数，用于正样本，右边画出了关于z的代价函数cost0(z)，函数的横轴是z，现在我们想一下怎么样才能使得这些代价函数变得更小呢？当有一个正样本的时候，y=1，那么仅当z大于等于1的时候，cost1(z)=0，换句话说，如果有一个正样本的时候，我们要θ的转置乘以x大于等于1，反之，如果y=0，我们看后面这一部分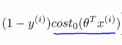。上述就是支持向量机很有趣的性质。这相当于在SVM中建立构建一个安全因子，一个安全距离

　　(1)如果有个正样本，比如y=1，我们要做的是 使得θ的转置乘以x大于等于0，就能进行正确的分类，因为如果θ的转置乘以x大于0，假设模型的预测结果就是0。同样的，如果有一个负样本，我们只需要使得θ的转置乘以x小于0，这样就能保证进行正确的分类。但是在支持向量机中，对此有更高的要求，不是恰好能正确分类就行了，θ的转置乘以x不是略大于0就可以了，我们要的，比如大于等于1，还有下面这个也是一样，我们要θ的转置乘以x小于-1，这就相当于在SVM中构建一个安全因子，构建一个安全距离，虽然logistic回归中也会做类似的事情，但是我们看看在支持向量机的情况下，这个因子会导致什么结果。接下来我们要来了将常数C设为一个非常大的值，

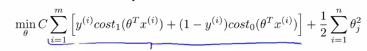
　　　(2)我们迫切希望找到一个值，使得第一项等于0，让我们在这种情况下来理解优化问题，也就是要怎么做才能使得第一项等于0，因为这时我们把C的值设置成为一个很大的值，这个例子能够让我们更加直观的理解支持向量机学习到的假设模型是怎么样的：

　　　　我们之前看到一个当有一个标签y=1的训练样本，如果要使得第一项为0的时候，那么就需要找到一个θ值，使得θ的转置乘以x(i)大于等于1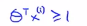，同样的如果有一个标签为0，为了使得代价函数cost0(z)=0，我们需要使得θ的转置乘以x(i)小于等于-1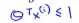，因此如果我们把优化问题看做是通过选择参数使得前面的这一项等于0，即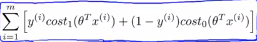,那么我们的优化函数能写成下面的形式，，如果y是正样本的时候，能够使得θ的转置乘以x(i)大于1，当y是负样本的时候，能够使得θ的转置乘以x(i)小于-1

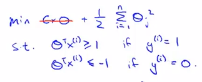
　　　　(3)基于上面的计算可以得到一个边界问题。具体可以观察这样的一个数据集，其中有正样本，也有负样本，这些数据线性可分，即存在一条直线，这条直线可以将正样本和负样本完美的划分开

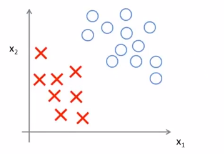
　　　　比如下面这条决策的边界，可以将正负样本划分开来，但是看起来不是很自然

 

 　　

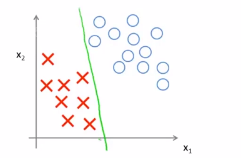
　　我们画一条更差的直线，比如下面这一条，刚好擦边将正负样本划分开来，下面这个图中，这两个变价看起来都不怎么好，但是SVM会选择下面这条边界，也就是黑色画的这条线，这条黑色的边界，比前面的绿色和红绳的边界要好很多，这条黑丝的看起来是更加稳健的决策边界。能够更好的将正样本和负样本分割开来，也就是说这条黑色的边界拥有更大的距离，这个距离吃个呢我间距

 　　

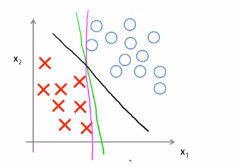
　　比如可以发现黑色的决策边界，和训练样本的最小距离要更大一些，这个距离叫做支持向量机距离，这使得支持向量机具有鲁棒性，因为在分离数据的时候会尽量用最大的间距去分离，因此有时候被称为最大间距分类器，这就是上面列出的优化问题的结果，

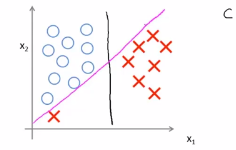
　　(4)关于大间距分类器，这里还有一点，大间距分类器是在C被设置的非常大的情况下得出的，给定下面的数据集，我们会选择一条这样的边界，用大间距来分开正样本和负样本，SVM要比这个大间距分类器更为复杂，尤其是当你使用大间距分类器的时候，这个时候的学习算法对异常点会非常敏感

　　

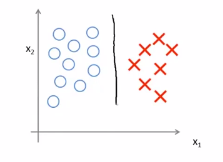
　　如下图所示，当你加一个样本点的时候，为了将样本点用大间距分开，可能最后学习到的边界是下图所示的边界，在这样的一个异常点的影响下，只因为这样的一个异常点就加入这样的一条紫色的分界面可能不是一个好主意，如果正则化常数C被设置的非常大，那么SVM就会将决策边界从黑线变为紫线，但是如果C比较小，不把C设置得很大，最后得到的还是这题的黑线，