机器学习与回归类算法
一、分类问题（监督学习，选择题）
1.根据数据样本上抽出的特征，判别其属于有限个类别中的哪一个
2.垃圾邮件识别(结果类别：1、垃圾邮件；2、正常邮件)
3.文本情感褒贬分析(结果类别：1、褒；2、贬)
4.图像内容识别(选择题：结果类别：1、喵星人；2、汪星人；3、人类；4、草拟马；5、都不是)
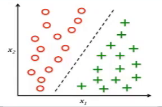
二、回归问题(监督学习，得分)
1.根据数据样本上抽取出的特征，预测连续值的结果
2.《芳华》票房值
3.魔都放假具体值
4.刘德华和吴彦祖的具体颜值得分
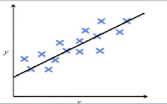
三、聚类问题(无监督学习)
1.根据数据样本上抽取出的特征，挖掘数据的关联模式
2.相似用户挖掘/社区发现
3.新闻聚类
四、强化问题：
1.研究如何基于环境而行动，以取得最大的预期利益
2.游戏最高得分
3.机器人完成的任务
五.下图来自周志华老师西瓜书
上图是一个监督学习。我们需要根据西瓜的色泽、根蒂和敲声来判断到底是一个好瓜还是一个坏瓜，最后的结果是两种情况，要么这个西瓜是一个好瓜，要么是一个坏瓜，依据是前面的三列。在上表中，每一行是一个西瓜样本，每一列是一个属性、特征，如西瓜的颜色、敲声和根蒂都是一个特征。即每一行是一个样本，每一列是一个特征。最后一列是我们的标记空间或者输出空间。最后学习到的是一个从x到y的映射，每一种模型只是映射不一样。
六、线性回归
1.何为线性回归
(1)有监督学习=>学习样本为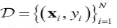
(2)输出/预测的结果yi为连续值变量(连续纸是一个回归问题)
(3)需要学习映射f:x->y(对于输入的x，可以输出连续值y)
(4)假定输入x和输出y之间有线性相关关系
(5)线性回归：准备了数据集(x,y)，用线性表示完成x到y之间的映射f，目的是学习出这样的一个映射，
2.测试/预测阶段
(1)对于给定的x，预测其输出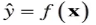
3.例子
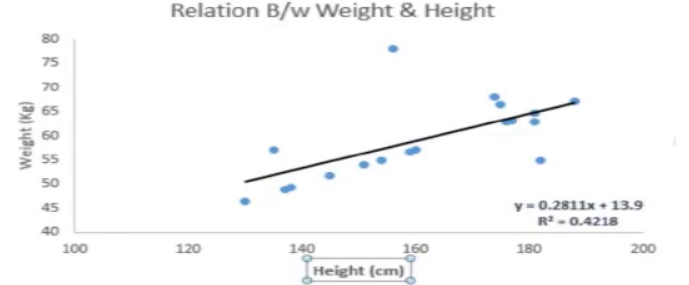
(1)你让一个六年级的孩子在不同同学具体体重多少的情况下，把班上的同学按照体重从轻到重排队。这个孩子会怎么做呢？她可能会通过观察大家的身高和体重来排队。
我们有一个样本，我们把身高和体重以横纵坐标的形式标到二维坐标系中，蓝色的坐标点是一个样本点，线性回归是根据图中随着身高增大，体重在不断增大的趋势，可以表示为下面一个简单的线性表达方式，用一条直线来拟合出一种变换，最终的线性回归如下图。
(2)房价预测：
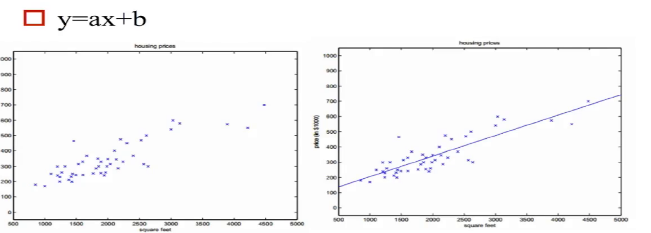
(1)通过y=ax+b来进行数据的拟合，得到下面的图：
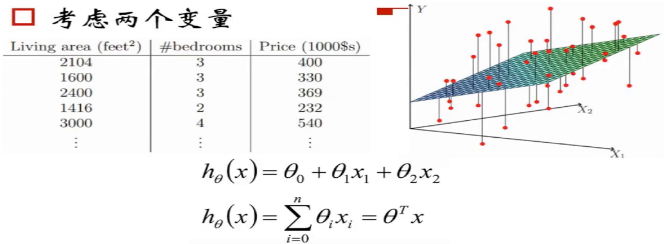
(2)当我们考虑多个变量的 时候，比如房屋面积，卧室个数的时候，拟合的直线就从二维中的直线成为了高维中的平面或者超平面，能得到下面的式子：
这个地方可以将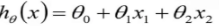 
写成向量的表达形式，
，
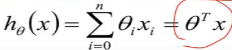这个地方θ和x都是一个列向量，然后将θ做转置操作，就成为了行向量，
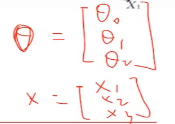
上面的θ转置和x做内积，最后的形式就是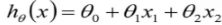
这种形式
(3)在大量的样本训练集中，总结出来的规律f用在这次未知的房价预估上，预估拿到结果
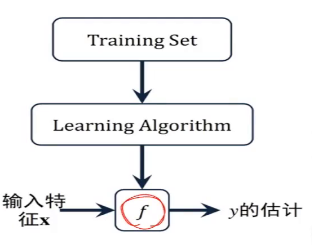
如上图，我们需要学习这里的训练集，得到一个x到y的映射f，这个f可以有各种形态，在线性回归中，我们给出了一个最简单的线性组合的形态，f(x)=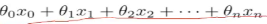
,对于这种形态，可以写成向量化的表达形式，在特征x中加一维X0=1来表示截距，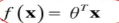
4.机器学习所有的方法都是：数据驱动=数据+模型(算法)
(1)模型=假设函数f(可能是一种计算的模型，可能是一种规则，可能是一种任何其他的东西)+优化(让θ一步步让模型朝着拟合更好拟合更准放入方向走)，不要把每个模型当做孤立的模型来看待。这些模型能不能用好，取决于能不能在大的架子下，在给你的学习方法的基础上完成优化。如何让θ朝着 让模型变得更好，拟合更准的方向去走，这部分叫做优化。
5.线性回归损失函数(loss function)
(0)在监督学习中，优化=loss function(损失函数，cost function代价函数)+optimizy优化算法
(1)找到最好的权重/参数[θ0,θ1,....θn]=θ
(2)怎么去衡量“最好”？
我们把x到y的映射函数f记为θ的函数hθ(x)
定义损失函数为：通过模型预估的结果是hθ(x)，真实值是y，是数据的标签。将预估的结果减去真实的结果，结果可正可负。平方就是数据之间的差值，除以m是数据的平均差距，这里的m是m个样本数，这里除以2是为了后面做数学优化的时候优化方便，没有过多的原因。这里x和y都是知道的只有θ是未知的
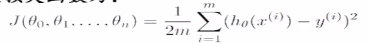
J(θ)是用来衡量模型好坏的量，不同的θ有不同的偏离量，我们要找到θ，使得Jθ是最小值，使得预估值和标准值之间的差值是最小值。如下图，当θ在不断变大的时候，就成为了右边图描述的变化，下图中凸函数的最低点是我们想要找到的最低点。当找到这个点的时候，就可以说明模拟效果很好。
对于多元情况，J(θ)的变化情况是下图的形式。目标数找到最小值，找到的是局部最低点。这个图是每取定一个θ，和标准答案差异的取值。
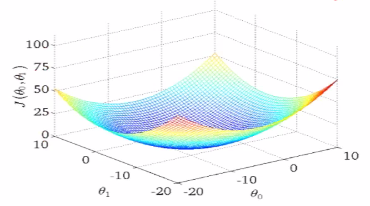
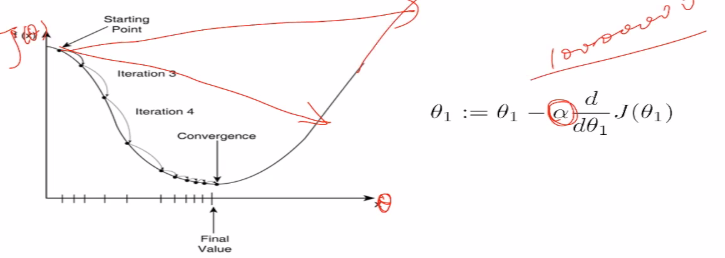
在计算机中，我们使用迭代法计算，优化=损失函数+优化算法，损失函数最小化的算法，我们使用梯度下降。
(3)梯度下降GD
逐步最小化损失函数的过程。如同下山，找准方向(斜率),每次迈出一小步，直至山底。
在起始位置开始，找到一个方向，会顺着方向向下滑动一段，然后再顺着方向再向下走，每一次都是这样的迭代，犹如一个下山的过程，找到最陡的方向往前迈出一步
对于二元的情况，下面是一个碗，放一个球，让其滚动，一层一层的截，就是等高线，球是垂直于等高线的方向向里面走动。
(4)多元梯度下降。下面的α是一个超参数，在模型学习之前需要敲定，需要自己选定。
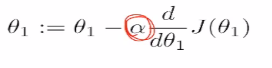
这里如果α过大，会直接跳过最低点，如果α非常大，
六、回归与欠/过拟合
0.通过多项式回归完成一个连续值的预估，标记了很多的样本点，最终的效果如上图。第一个线性模型不能够拟合好所有的样本，拟合能力很差，以至于不能拟合好所有的样本点。第二个抛物线可以穿过所有的点，而且离所有的点都比较近，第三图高次曲线能够很好的穿过所有的点，
1.比较模型的好坏，就是比较谁的模型泛化能力更好，学习到的模式会更通用一点。
2.过拟合问题：如果我们有非常多的特征/模型很复杂，我们的假设函数曲线可以对原始数据拟合非常好
，但是丧失了一般性，从而导致对新给的待预测样本，预测效果差。
3.所有的模型都有可能存在过拟合的风险，意味着有更强的能力，但也更可能无法无天，眼见不一定为实，你看到的内容不一定为全部真实的数据分布，死记硬背不太好。
4.正则化。
(0)在这之前的损失函数长成这个样子。只要模型拟合的很好就可以，但是抖动非常大，就说明非常的不平稳，等到新的样本来的时候，模型就挂掉了。
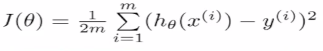
(1)控制参数幅度，不能让模型“无法无天”
(2)限制参数搜索空间，下式中，后面加的一项是θ的幅度，人是超参数，给后面这个幅度加多大的惩罚。这里误差项样本要加到m是因为有m个样本，惩罚项加到n是因为有n个θ，即有n个特征
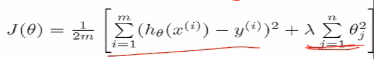
七、逻辑斯蒂回归
1.解决分类问题。
(1)线性回归+阈值。下图中横坐标是肿瘤的大小，纵坐标是是否是一个恶性肿瘤，现在肿瘤大小在0.5左侧就是良性肿瘤，在0.5右侧就是恶性肿瘤。
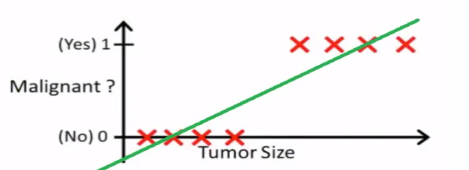
但是上面的这个方法并不是一个很好的方法，如果来了两个异常值，肿瘤大小非常大，在这种情形下显然是恶性肿瘤，再去做线性回归会发现这条直线被拉偏了，因为它要兼顾到所有的样本，拉偏之后再取0.5做阈值，就发现有两个样本被错误的划分，健壮性不够，对噪声不太敏感。
(2)sigmoid函数，数学特性很好。
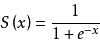
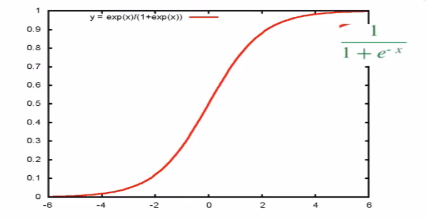
(3)g(x)的导函数：如果需要求导，可以一步求出来。
g`(x)=g(x)[1-g(x)]
(4)所有的分类问题，本质上式在空间中找到一个决策边界，完成这里的决策。如下图可以将样本点进行划分。
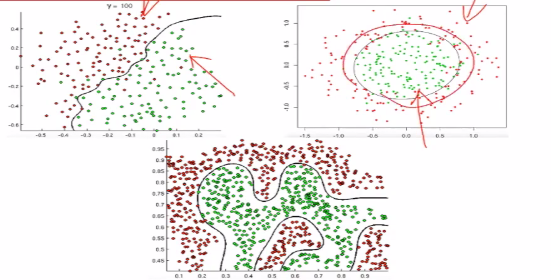
(5)线性判定边界。如何由线性回归得到拟合的直线或者曲线变成这样的一条决策边界
直线上方的点 代进去会大于0，
(6)非线性判定边界。对于这个图，圆外的点是大于0的，圆内的点是小于0的，对应于sigmoid函数，圆外的是大于0.5的，圆内的点是小于0.5的
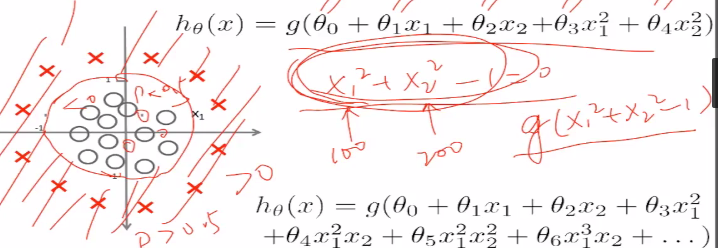
损失函数：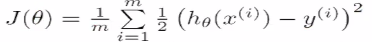
的数学特性不好，如下
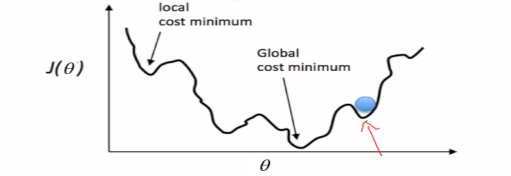
有很多最低点，损失函数凹凸不平，特性不好。我们使用下面的损失函数，
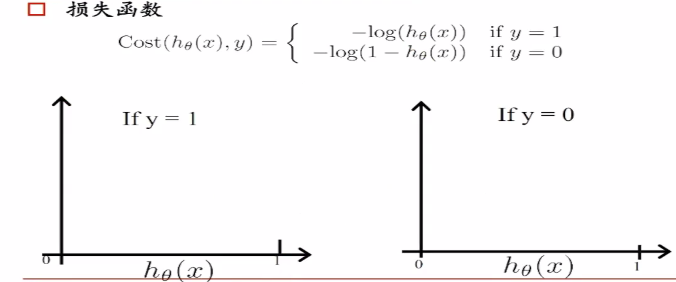
hθ是属于正样本的概率p，hθ(x)=p，我们希望概率p越大越好，logp越大越好，-logp越小越好，损失函数如下。
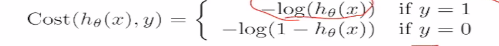
当它是负样本的时候，希望log(1-p)越大越好，-log(1-p)越小越好。同理如果是正样本的时候，我们希望log(1-p)越大越好。一个0到1之间的数，越乘越小，我们将其变为加法。于是就得到下面的损失函数(二院交叉熵损失)：
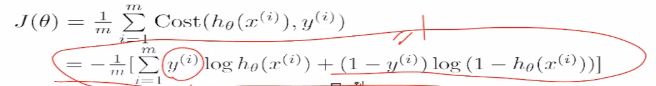
加上正则化项如下：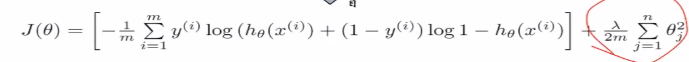 
2.多分类：
(1) one vs one 用二分类来解决多分类，在任意两个人类之间构建分类器，
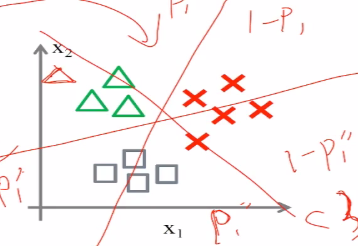
构建多个二分类器和构建一个多分类器，
(2) one vs rest，同样会构建三个分类，是不是小三角形，是不是小叉叉，是不是小方块，在取得了三个分类器之后，会取得最大的概率p
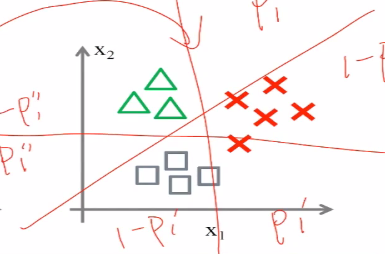
八、LR应用经验
1.LR<SVM/GBDT/RandomForest>
(1)模型没有好坏之分
LR能以概率的形式输出结果，而非只有0,1判定
LR可解释性强，可控度高
训练快，feature engineering之后效果赞
因为结果是概率，可以做ranking model
添加feature太简单
(2)应用
CRT预估/推荐系统的learning to rank/各种分类场景
某搜索引擎厂的广告CTR预估基线版是LR
某电商搜索排序/广告CTR预估基线版是LR
某电商的购物搭配推荐使用了大量的LR
某现在一天广告赚1000w+的新闻app排序基线是LR
