深度学习初步
一、背景介绍
1.深度学习应用
二、神经网络非线性能力及原理
0.线性分类器得分函数
(1)假设函数:x到y的映射f。 这个f可以是多种表现形式,比如逻辑回归,决策树,随机森林以及xgboost是另外的一种表达形式,这里的神经网络是另外的表达。
(2)我们要的结果是要结果和标准答案更加接近,损失函数是用来衡量 f(x)好坏的一个量,和标准答案之间的差异。
(3)图像要一种呈现方式来表达,以数字化的表达形式送给神经网络来学习
(4)如下图像,[32 x 32 x 32]表示图像的宽和高都有32个像素点,3表示有R,G,B三个不同颜色的通道

当图像送进来之后,我们需要对图像x进行某种变换w,得到的结果是10种不同的类别,分别拿到10个不同结果的得分,拿到一个映射函数,这个映射函数能从数据映射到一个10维的得分向量,我们将32x32x10的矩阵拉长为一个一条向量,在矩阵中的做法叫做flating,形成了32x32x3x1的列向量,这里我们要得到10个类别的得分向量,就需要将w设置成为10x3072的矩阵,然后与x(3072x1)得到得到有10行数据的行向量。

这里的w就是参数,或者说是权重,是可以调节的内容。如下面W是3行4列的数据,x是一个4行1列的数据,就是32x32x3的图像,拉成一条,是一个3072维的向量,最终的得分类别有3个。b是一个偏置项,最后得分向量有3行。有时候将在x下面再加1,然后再w后面加一项偏置项
1.感知器与逻辑门
2.强大的空间非线性切分能力
3.网络表达力与过拟合问题
4.BP算法与SGD、
5.损失函数loss function(别称:代价函数cost function/客观度objective)
(1)给定W,可以由像素映射到类目得分。
(2)可以调整参数/权重W,使得映射的结果和实际类别吻合
(3)损失函数是用来衡量吻合度的
6.损失函数1:hinge loss(合页损失)/支持向量机损失,是一个可以满足的损失函数(只要所有的错误的类都在安全警戒线之外损失就是0),用来衡量和标准答案之间的差异到底有多大
(0)因为是线性模型,所以可以简化为:
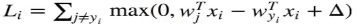
上面公式中,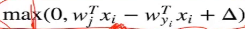 表示某个类别的得分和真实值的得分之间的惩罚,遍历所有非真实类别的其他的类别的损失,全部都加在一起,
表示某个类别的得分和真实值的得分之间的惩罚,遍历所有非真实类别的其他的类别的损失,全部都加在一起,
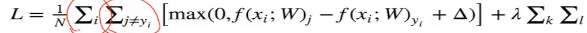
这里∑i是对我要学习的所有N张图片进行学习,对每张图片上计算出来的损失进行一个求和,
(1)对于训练集中的第i张图片数据xi
(2)在w下会有一个得分结果向量f(xi,W)
(3)在j类的得分为我们记作f(xi,w)j
(4)那么在该样本上的损失我们有下面公式计算得到
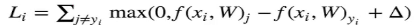
(5)假设我们有3个类别,而得分函数计算某张图片的得分为f(xi,W)=[13,-7,11],而实际结果是第一类(yi=0)。假设Δ=10。上面的公式把错误类别(j!=yi)都遍历了一遍,求值家和:
Li=max(0,-7-13+10)+max(0,11-13+10)
7.得分向量归一化:标准答案是1 0 0,分数越高的概率越高。

8.损失函数2:交叉熵损失(softmax分类器),可以做归一化
(0)交叉熵损失本质上是衡量和标准答案概率向量之间概率的差异到底有多大,交叉熵损失永远有值
(1)对于训练集中的第i张图片数据x,在w下会有一个得分结果向量fyi,则损失函数记作:
 或者
或者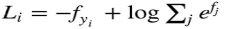
一般在工程中这么计算:
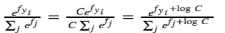
在标准答案中,标准答案是1,其他的概率是0。我希望pi越大越好,那么logpi越大越好,那么Li越小越好。
三、通用学习框架
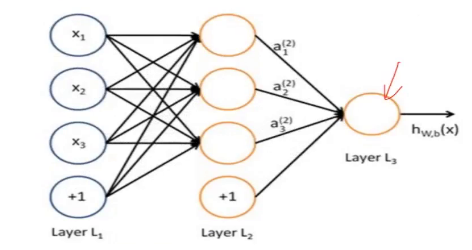
1.一般神经网络结构的结构。多层神经网络DNN(MLP,FNN)
(1)输入层
(2)隐层
(3)输出层 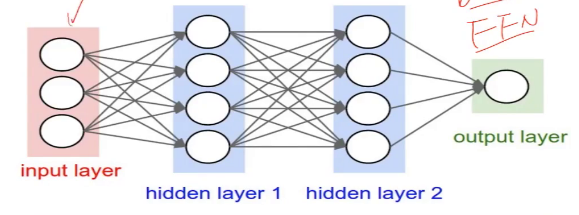
(4)从逻辑回归到神经元“感知器”(神经元)
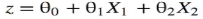
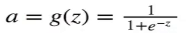 (sigmoid函数)
(sigmoid函数)

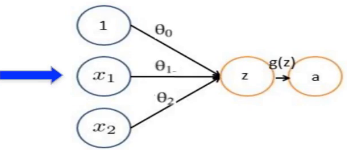
(4)sigmoid函数求导:
g`(z)=g(z)[1-g(z)]
(5)添加少量的隐藏层===>浅层神经网络
2.神经元完成逻辑与
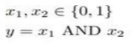
(1)1 AND 1 = 1
1 AND 0 = 0
0 AND 1 = 0
0 AND 0 = 0
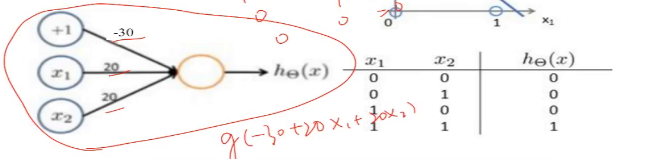
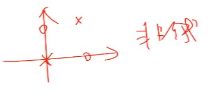
对于下面这种样本,使用非线性分类器是分不开样本点的。解决的办法是通过线性分类器组合得到。
3.逻辑或
1 OR 1 = 1
1 OR 0 = 1
0 OR 1 = 1
0 OR 0 = 0

4.对线性分类器的AND和OR的组合
完美对平面样本点分布进行分类
线性分类器AND和OR
通过如下神经元的形式进行表达,发现有很多的线性分类器。 通过AND的方法划分出所有的样本,然后通过OR方法将所有的样本区域连接起来。

5.神经网络分类:
(1)无隐层(即线性分类器 ):由一超平面分成两个
(2)单隐层:AND操作:开凸区域或者闭凸区域
(3)双隐层:任意形状(复杂度由单元数目决定)

(4)理论上说单隐层神经网络可以逼近任何连续函数(只要隐层的神经元个数足够多)
(5)虽然从数学上来看表达能力一致,但是多隐层的神经网络比单隐层神经网路工程效果要好很多
(6)对于一些分类数据,3层神经网络的效果优于两层神经网络,但是如果层数的不断的增加,对最后效果的帮助就没有那么大的跳变了。
(7)图像数据比较特殊,是一种深层(多层次)的结构化数据,深层次的卷积神经网络,能够更加充分和准确地把这些层级信息表达出来。
(8)提升隐层层数或者隐层神经元个数,神经网络“容量”会变大,空间表达力会变强

(9)过多的隐层和神经元节点,会带来拟合问题,学习能力太强。
(10)不要试图通过降低神经网络参数量来减缓过拟合,用正则化或者dropout。会搭建有一定深度的神经网络,但是会用正则化的方式来控制。
四、神经网络的结构和优化
1.神经网络由输入层、输出层和中间的隐层组成,俗称MLP多层感知器,在输入层和输出层之间有若干个隐层,每个隐层会做一个计算wx+b,但是在这个基础上,我们通常会加上一个非线性变换的函数sigmoid。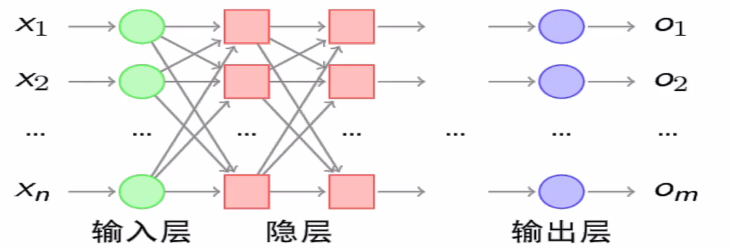
2.传递函数(激活函数):S函数(sigmoid) VS 双S函数,激活函数本质上就是数学上非线性变换的函数。在每一层的线性变换之后,都会接一层非线性变换函数。之所有要用非线性变换的函数,非线性变换的函数有很多不同的形态,我们一般挑选数学特性比较好的函数,多个线性本质上就是一个线性,所以后面会添加一个非线性

五、BP算法(反向传播算法)
0.BP算法也叫δ算法。以3层感知器为例:
把问题不断地往前剥离开来,找到哪个东西会最初的影响最后的结果,然后再去做修正。
1.“正向传播”求损失,“反向传播”回传误差
2.根据误差信号修正每层的权重
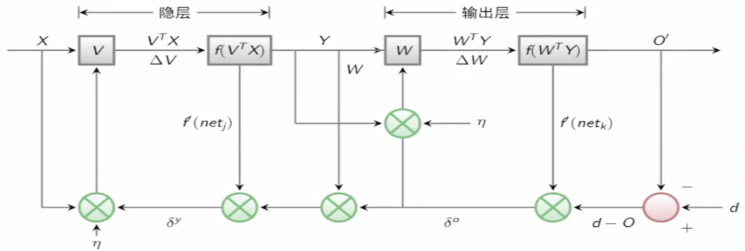
3.假设函数:完成x到y的映射
4.损失函数:

六、神经网络之SGD
1.误差E有了,怎么调整权重让误差不断减小?
2.E是权重w的函数,我们需要找到使得函数值最小的W
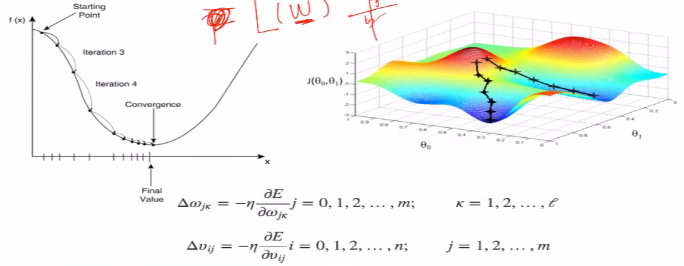
3.前向(前馈)运算

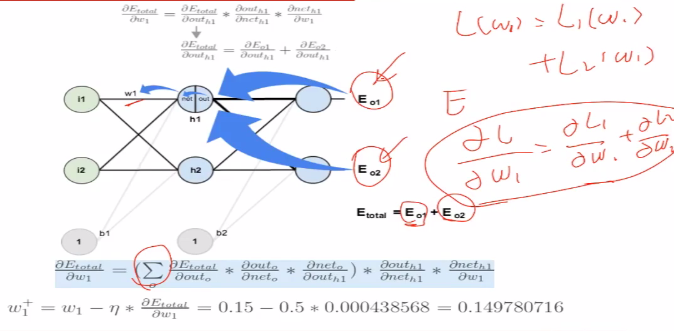
通过求导的链式法则进行求导

七、代码与示例
1.Tensorflow多层感知器非线性切分
2.神经网络分类示例
3.Google Wide&&Deep Model


 浙公网安备 33010602011771号
浙公网安备 33010602011771号