特征分解和奇异值分解

1.特征分解

　　将矩阵分解成一组特征向量和特征值

2.方阵 A 的特征向量（eigenvector）

　　与 A 相乘后相当于对该向量进行缩放的非零向量 v

　　Av = λv

　　标量 λ 被称为这个特征向量对应的特征值（eigenvalue）　

　　如果 v 是 A 的特征向量，那么任何缩放后的向量 sv (s ∈ R，s ̸= 0) 也是 A 的特征向量。此外，sv 和 v 有相同的特征值。基于这个原因，通常我们只考虑单位特征向量

　　假设矩阵 A 有 n 个线性无关的特征向量 {v (1) ,...,v (n) }，对应着特征值{λ 1 ,...,λ n }。我们将特征向量连接成一个矩阵，使得每一列是一个特征向量：

　　V = [v (1) ,...,v (n) ]. 类似地，我们也可以将特征值连接成一个向量 λ = [λ 1 ,...,λ n ] ⊤ 。因此 A 的特征分解（eigendecomposition）可以记作

　　　　A = Vdiag(λ)V −1

　　所有特征值都是正数的矩阵被称为正定（positive definite）；所有特征值都是非负数的矩阵被称为半正定（positive semidefinite）。

　　同样地，所有特征值都是负数的矩阵被称为负定（negative definite）；所有特征值都是非正数的矩阵被称为半负定（negative semidefinite）

3.奇异值分解

　　矩阵分解为奇异向量（singular vector）和奇异值（singular value）

　　A 分解成三个矩阵的乘积

　　　　

 

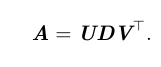
　　A 是一个 m×n 的矩阵，那么 U 是一个 m×m 的矩阵，D 是一个 m×n的矩阵，V 是一个 n × n 矩阵。

　　矩阵 U 和 V 都被定义为正交矩阵，而矩阵 D 被定义为对角矩阵

　　对角矩阵 D 对角线上的元素被称为矩阵 A 的奇异值（singular value）。矩阵U 的列向量被称为左奇异向量（left singular vector），矩阵 V 的列向量被称右奇异向量（right singular vector）

　　A 的左奇异向量（left singular vector）是 AA ⊤ 的特征向量。A 的右奇异向量（right singularvector）是 A ⊤ A 的特征向量。

　　A 的非零奇异值是 A ⊤ A 特征值的平方根，同时也是AA ⊤ 特征值的平方根