特殊类型的矩阵和向量

1.对角矩阵（diagonal matrix）

　　只在主对角线上含有非零元素，其他位置都是零

　　对角方阵的逆矩阵存diag(v) −1 = diag([1/v 1 ,...,1/v n ] ⊤ )

2.对称（symmetric）矩阵

　　转置和自己相等的矩阵

　　　　A = A ⊤　　

3.单位向量（unit vector）

　　具有单位范数（unit norm）的向量　

　　　　　

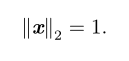
4.正交

　　如果 x ⊤ y = 0，那么向量 x 和向量 y 互相正交（orthogonal）

　　如果两个向量都有非零范数，那么这两个向量之间的夹角是 90 度

　　如果这些向量不仅互相正交，并且范数都为 1，那么我们称它们是标准正交（orthonormal）

5.正交矩阵

　　行向量和列向量是分别标准正交的方阵

　　A ⊤ A = AA ⊤ = I

　　A −1 = A ⊤