线性相关和生成子空间

1.线性组合（linear combination）

　　如果 x 和y 都是某方程组的解，则z = αx + (1 − α)y （其中 α 取任意实数）也是该方程组的解。

　　为了分析方程有多少个解，我们可以将 A 的列向量看作是从原点（origin）（元素都是零的向量）出发的不同方向，确定有多少种方法可以到达向量 b。

　　在这个观点下，向量 x 中的每个元素表示我们应该沿着这些方向走多远，即 x i 表示我们需要沿着第 i 个向量的方向走多远：

　　这种操作被称为线性组合　。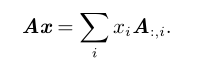　

　　形式上，一组向量的线性组合，是指每个向量乘以对应标量系数之后的和，即：

　　　　　　

 

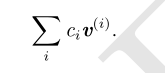
　　一组向量的生成子空间（span）是原始向量线性组合后所能抵达的点的集合。

　　确定 Ax = b 是否有解相当于确定向量 b 是否在 A 列向量的生成子空间中。这个特殊的生成子空间被称为 A 的列空间（column space）或者 A 的值域（range）。

　　不等式 n ≥ m 仅是方程对每一点都有解的必要条件。

　　线性相关（linear dependence）

　　　　列向量可能是冗余的，即一组向量中有一部分向量是相同的。

　　线性无关（linearly independent）

　　　　如果一组向量中的任意一个向量都不能表示成其他向量的线性组合，那么这组向量被称为线性无关。

　　矩阵必须是一个方阵（square），即 m = n，并且所有列向量都是线性无关的是矩阵有逆矩阵的充分必要条件。

　　一个列向量线性相关的方阵被称为奇异的（singular）。