标量、向量、矩阵和张量

1.标量（scalar）：

　　一个标量就是一个单独的数，它不同于线性代数中研究的其他大部分对象（通常是多个数的数组）。

　　我们用斜体表示标量。标量通常被赋予小写的变量名称。

　　介绍标量时，会明确它们是哪种类型的数。

2.向量（vector）：

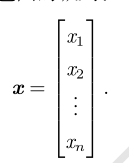
　　一个向量是一列数。这些数是有序排列的。

　　通过次序中的索引，我们可以确定每个单独的数。通常我们赋予向量粗体的小写变量名称，比如 x。

　　需要注明存储在向量中的元素是什么类型。

　　常见表示类型：

　　　　　　　　

　　有时我们需要索引向量中的一些元素。在这种情况下，我们定义一个包含这些元素索引的集合，然后将该集合写在脚标处。

　　比如，指定 x 1 ，x 3 和 x 6 ，我们定义集合 S = {1,3,6}，然后写作 x S 。

　　我们用符号－表示集合的补集中的索引。

　　比如 x −1 表示 x 中除 x 1 外的所有元素，x −S 表示 x 中除 x 1 ，x 3 ，x 6 外所有元素构成的向量。

3.矩阵（matrix）：

　　矩阵是一个二维数组，其中的每一个元素被两个索引而非一个所确定。我们通常会赋予矩阵粗体的大写变量名称，比如 A。

　　如果一个实数矩阵高度为 m，宽度为 n，那么我们说 A ∈ R m×n 。我们在表示矩阵中的元素时，通常以不加粗的斜体形式使用其名称，索引用逗号间隔。

　　比如，A 1,1 表示 A 左上的元素，A m,n 表示 A 右下的元素。

　　我们通过用 “:’’ 表示水平坐标，以表示垂直坐标 i 中的所有元素

　　比如，A i,: 表示 A 中垂直坐标 i 上的一横排元素。

　　这也被称为 A 的第 i 行（row）。同样地，A :,i 表示 A 的第 i 列（column）。

　　常见形式：

　　　　　　

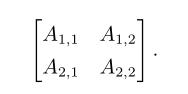
　　有时我们需要矩阵值表达式的索引，而不是单个元素。在这种情况下，我们在表达式后面接下标，但不必将矩阵的变量名称小写化。

　　比如，f(A) i,j 表示函数f 作用在 A 上输出的矩阵的第 i 行第 j 列元素。

4.张量（tensor）：

　　在某些情况下，我们会讨论坐标超过两维的数组。一般地，一个数组中的元素分布在若干维坐标的规则网格中，我们将其称之为张量。

　　我们使用字体 A 来表示张量 “A’’。张量 A 中坐标为 (i,j,k) 的元素记作 A i,j,k 。