深度模型中的优化

1.随机梯度下降

　　

　　　　保证SGD收敛的一个充分条件是

　　　　　　

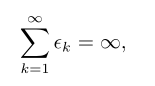
　　　　线性衰减学习率直到第 τ 次迭代：

　　　　　　

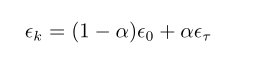
　　　　　　其中 α =k/τ 。在 τ 步迭代之后，一般使 ϵ 保持常数

　　　　　　通常 τ 被设为需要反复遍历训练集几百次的迭代次数。通常 ϵ τ 应设为大约 ϵ 0 的 1%。主要问题是如何设置 ϵ 0 。若 ϵ 0 太大，学习曲线将会剧烈振荡，代价函数值通常会明显增加。

　　　　　　温和的振荡是良好的，容易在训练随机代价函数（例如使用Dropout的代价函数）时出现。如果学习率太小，那么学习过程会很缓慢

　　　　动量算法引入了变量 v 充当速度角色——它代表参数在参数空间移动的方向和速率

　　　　　　

　　　　步长大小为

　　　　　　

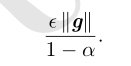
　　　　动量的超参数视为1/(1−α)

　　Nesterov 动量

　　　　

　　　　

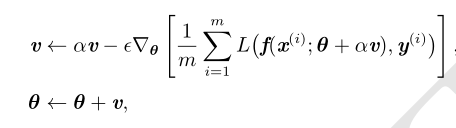
　　　　　　Nesterov 动量将额外误差收敛率从 O(1/k)（k 步后）改进到 O(1/k 2 )

2.参数初始化策略

　　标准初始化

　　　　

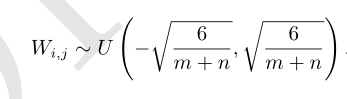
3.自适应学习率算法

　　AdaGrad

　　　　

 　　RMSProp

　　　　修改 AdaGrad 以在非凸设定下效果更好，改变梯度积累为指数加权的移动平均

　　　　　　

　　　　　　　

　　Adam

　　　　

 4.二阶近似方法

　　

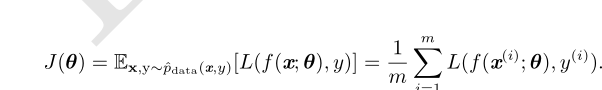
　　牛顿法

　　　　牛顿法是基于二阶泰勒级数展开在某点 θ 0 附近来近似 J(θ) 的优化方法

　　　　　　

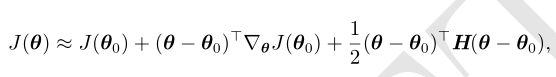
　　　　牛顿参数更新规则

　　　　　　

　　　　正则化策略包括在Hessian矩阵对角线上增加常数 α

　　　　　　

　　　　　　

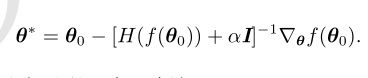
　　共轭梯度

　　　　共轭梯度是一种通过迭代下降的共轭方向（conjugate directions）以有效避免Hessian矩阵求逆计算的方法

　　　　如果 d ⊤t H d t−1 = 0，其中 H 是Hessian矩阵，则两个方向 d t 和 d t−1 被称为共轭的

　　　　计算 β t 的流行方法是

　　　　　　 Fletcher-Reeves

　　　　　　　　

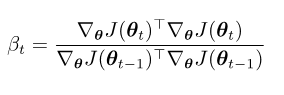
　　　　　　 Polak-Ribière

　　　　　　　　

 　　　　　　

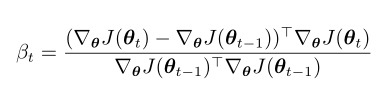
5.优化策略和元算法

　　标准化 H

　　　　

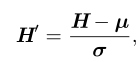
　　　　其中 µ 是包含每个单元均值的向量，σ 是包含每个单元标准差的向量

　　　　

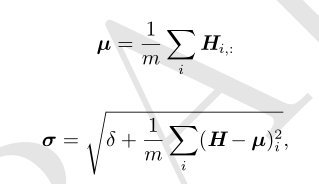
　　　　　　δ 是个很小的正值，比如 10 −8 ，以强制避免遇到√ z 的梯度在 z = 0 处未定义的问题

　　　　　　

　　坐标下降

　　　　相对于某个单一变量 x i 最小化 f(x)，然后相对于另一个变量 x j 等等，反复循环所有的变量，我们会保证到达（局部）极小值。这种做法被称为坐标下降

　　　　块坐标下降（blockcoordinate descent）是指对于某个子集的变量同时最小化

　　监督预训练

　　　　训练简单模型求解简化问题的方法统称为预训练（pretraining）

　　　　贪心算法（greedy algorithm）将问题分解成许多部分，然后独立地在每个部分求解最优值

　　　　贪心算法也可以紧接一个精调（fine-tuning）阶段，联合优化算法搜索全问题的最优解