深度前馈网络

1.深度前馈网络

　　定义了一个映射 y = f(x;θ)，并且学习参数 θ 的值，使它能够得到最佳的函数近似

2.这种模型被称为前向（feedforward）

　　在模型的输出和模型本身之间没有反馈（feedback）连接

3.深度（depth）

　　模型的层数

4.隐藏层（hidden layer）

　　隐藏层的维数决定了模型的宽度（width）

5.线性模型

　　逻辑回归和线性回归

　　被局限在线性函数里

　　扩展线性模型来表示 x 的非线性函数

　　 ϕ(x) 上，这里 ϕ 是一个非线性变换

　　如何选择映射 ϕ

　　　　使用一个通用的 ϕ

　　　　手动地设计 ϕ

　　　　深度学习的策略是去学习 ϕ

　　　　　　y = f(x;θ,w) =ϕ(x;θ) ⊤ w

6.学习 XOR

　　　异或函数

7.基于梯度的学习

　　代价函数

　　　　交叉熵

　　　　使用最大似然学习条件分布

　　　　　　负的对数似然

　　　　　　

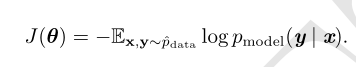
　　　　均方误差

　　均方误差

　　输出单元

　　　　用于高斯输出分布的线性单元

　　　　用于 Bernoulli 输出分布的 sigmoid 单元

　　　　用于 Multinoulli 输出分布的 softmax 单元

　　隐藏单元

　　　　h i =g(z,α) i = max(0,z i ) + α i min(0,z i )

　　　　整流线性单元

　　　　　　整流线性单元使用激活函数 g(z) = max{0,z}

　　　　大多数的隐藏单元都可以描述为接受输入向量 x，计算仿射变换 z = W ⊤ x + b，然后使用一个逐元素的非线性函数 g(z)。大多数隐藏单元的区别仅仅在于激活函数 g(z) 的形式。

　　　　绝对值整流

　　　　　　g(z) = |z|

　　　　　　图像中的对象识别

　　　　渗漏整流线性单元（Leaky ReLU）

　　　　　　将 α i 固定成一个类似 0.01 的小值

　　　　参数化整流线性单元（parametric ReLU）或者 PReLU

　　　　　　将α i 作为学习的参数

　　　　maxout 单元（maxout unit）

　　　　　　maxout 单元将 z 划分为每组具有 k 个值的组，而不是使用作用于每个元素的函数 g(z)。每个maxout 单元则输出每组中的最大元素

　　　　　　

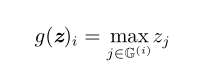
　　　　logistic sigmoid与双曲正切函数

　　　　　　g(z) = σ(z)

　　　　　　g(z) = tanh(z)

　　　　　　 tanh(z) = 2σ(2z) − 1

　　　　softplus函数

　　　　　　g(a) = ζ(a) = log(1 + e a )

8.架构设计

　　架构（architecture）一词是指网络的整体结构：它应该具有多少单元，以及这些单元应该如何连接

　　这些链式架构中，主要的架构考虑是选择网络的深度和每一层的宽度

　　万能近似性质和深度

　　　　线性模型，通过矩阵乘法将特征映射到输出，顾名思义，仅能表示线性函数

　　　　　　它具有易于训练的优点，因为当使用线性模型时，许多损失函数会导出凸优化问题

　　　　万能近似定理

　　　　　　一个前馈神经网络如果具有线性输出层和至少一层具有任何一种 ‘‘挤压’’ 性质的激活函数（例如logistic sigmoid激活函数）的隐藏层，

　　　　　　只要给予网络足够数量的隐藏单元，它可以以任意的精度来近似任何从一个有限维空间到另一个有限维空间的 Borel 可测函数

　　　　　　万能近似定理说明了，存在一个足够大的网络能够达到我们所希望的任意精度，但是定理并没有说这个网络有多大

　　层与层之间连接

　　　　默认的神经网络层采用矩阵 W 描述的线性变换，每个输入单元连接到每个输出单元

　　反向传播和其他的微分算法

　　　　前向传播（forward propagation）

　　　　　　输入 x 提供初始信息，然后传播到每一层的隐藏单元，最终产生输出 ˆ y

　　　　　　产生一个标量代价函数 J(θ)

　　反向传播（back propagation）算法　　

　　　　允许来自代价函数的信息通过网络向后流动，以便计算梯度

　　　　反向传播仅指用于计算梯度的方法，而另一种算法，例如随机梯度下降，使用该梯度来进行学习

　　　　最常需要的梯度是代价函数关于参数的梯度，即∇ θ J(θ)

　　计算图

　　　　变量

　　　　　　每一个节点来表示一个变量。变量可以是标量、向量、矩阵、张量、或者甚至是另一类型的变量

　　　　操作（operation）

　　　　　　操作是指一个或多个变量的简单函数

　　微积分中的链式法则

　　　　用于计算复合函数的导数。反向传播是一种计算链式法则的算法，使用高效的特定运算顺序

　　　　f(g(x)) = f(y)。那么链式法则是说

　　　　　　

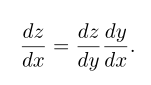
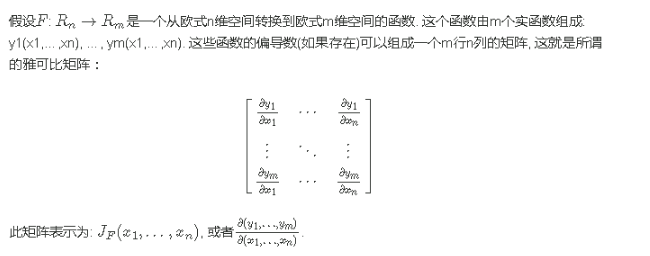
　　　　可以将这种标量情况进行扩展。假设 x ∈ R m ,y ∈ R n ，g 是从 R m 到 R n 的映射，f 是从 R n 到 R 的映射如果 y = g(x) 并且 z = f(y)，那么

　　　　　　

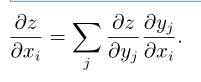
　　　　　　使用向量记法，可以等价地写成

　　　　

　　　　　　

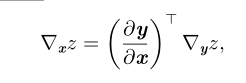
　　　　　　　这里∂y/∂x是 g 的 n × m 的 Jacobian 矩阵(雅可比矩阵)

　　　　　　　　

　　　　　　变量 x 的梯度可以通过 Jacobian 矩阵 ∂y/∂x和梯度 ∇ y z 相乘来得到

　　　　　张量的链式法则,如果 Y = g(X) 并且 z = f(Y)，那么

　　　　　　

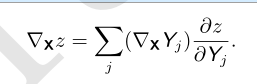
　　　递归地使用链式法则来实现反向传播

　　　　　　直接写出某个标量关于计算图中任何产生该标量的节点的梯度的代数表达式

　　　　　　任何计算梯度的程序都需要选择是存储这些子表达式还是重新计算它们几次

　　全连接 MLP 中的反向传播计算