估计、偏差和方差

1.点估计

　　令 {x (1) ,...,x (m) } 是 m 个独立同分布（i.i.d.）的数据点。点估计（point esti-mator）或统计量（statistics）是这些数据的任意函数：

　　　

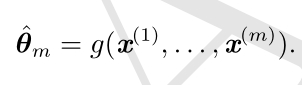
　　　　良好的估计量的输出会接近生成训练数据的真实参数 θ

　　点估计也可以指输入和目标变量之间关系的估计。我们将这种类型的点估计称为函数估计

2.偏差

　　估计的偏差被定义为：

　　　　

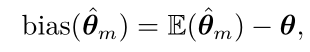
　　　　其中期望作用在所有数据（看作是从随机变量采样得到的）上，θ 是用于定义数据生成分布的 θ 的真实值

　　　　如果 bias( ˆ θ m ) = 0，那么估计量ˆθ m 被称为是无偏（unbiased），这意味着 E( ˆ θ m ) = θ。

　　　　如果 lim m→∞ bias( ˆ θ m ) = 0，那么估计量ˆθ m 被称为是渐近无偏（asymptotically unbiased），这意味着 lim m→∞ E( ˆ θ m ) = θ

3.方差和标准差

　　估计量的方差（variance）就是一个方差

　　　　　

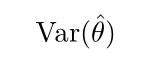
　　方差的平方根被称为标准差（standard error），记作SE( ˆ θ)

　　均值的标准差被记作

　　　　

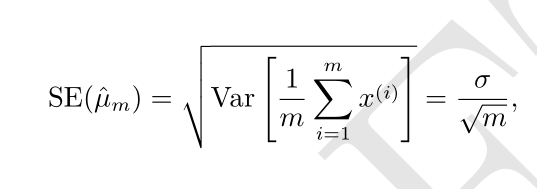
　　均值 ˆ µ m 为中心的 95% 置信区间是

　　　　

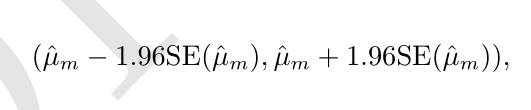
　　　　算法 A 比算法 B 好，是指算法 A 的误差的 95% 置信区间的上界小于算法 B的误差的 95% 置信区间的下界

　　均方误差

　　　　

 

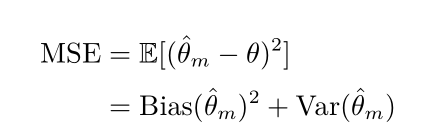
4.一致性 

　　数据点的数量 m 增加时，点估计会收敛到对应参数的真实值

　　　　

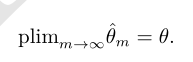
　　　　符号 plim 表示依概率收敛，即对于任意的 ϵ > 0，当 m → ∞ 时，有 P(| ˆ θ m − θ| >ϵ) → 0

　　几乎必然收敛（almost sureconvergence）是指当 p(lim m→∞ x (m) = x) = 1 时，随机变量序列 x (1) ，x (2) ，... 收敛到 x

　　一致性保证了估计量的偏差会随数据样本数目的增多而减少