基于梯度的优化方法

1.目标函数（objective function）或准则（criterion）

　　要最小化或最大化的函数

　　最小化时，我们也把它称为代价函数（cost function）、损失函数（loss function）或误差函数（error function）

　　一个上标 ∗ 表示最小化或最大化函数的 x 值。如我们记 x ∗ =argminf(x)

2.梯度下降（gradient descent）

　　将 x 往导数的反方向移动一小步来减小 f(x)

　　f(x − ϵsign(f ′ (x)))

　　f ′ (x) = 0 的点称为临界点（critical point）或驻点（stationary point）

　　一个局部极小点（local minimum）意味着这个点的 f(x) 小于所有邻近点，因此不可能通过移动无穷小的步长来减小f(x)

　　一个局部极大点（local maximum）意味着这个点的 f(x) 大于所有邻近点，因此不可能通过移动无穷小的步长来增大 f(x)

　　临界点既不是最小点也不是最大点。这些点被称为鞍点（saddle point）

　　　　

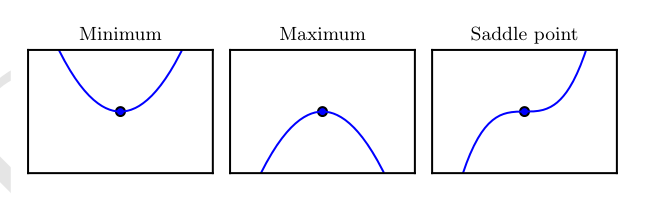
　　使 f(x) 取得绝对的最小值（相对所有其他值）的点是全局最小点（global minimum）

　　最小化具有多维输入的函数：f : R n → R。针对具有多维输入的函数，我们需要用到偏导数（partial derivative）的概念

　　偏导数衡量点 x 处只有 x i增加时 f(x) 如何变化

　　梯度（gradient）是相对一个向量求导的导数:f 的导数是包含所有偏导数的向量，记为 ∇ x f(x)

　　梯度的第i个元素是 f 关于 x i 的偏导数。在多维情况下，临界点是梯度中所有元素都为零的点

　　在 u（单位向量）方向的方向导数（directional derivative）是函数 f 在 u 方向的斜率

　　方向导数是函数 f(x + αu) 关于 α 的导数（在 α = 0 时取得）。使用链式法则，我们可以看到当 α = 0 时，∂/∂α  f(x + αu) = u⊤ ∇ x f(x)

　　计算方向导数

　　　　

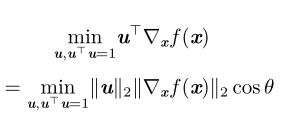
　　　　其中 θ 是 u 与梯度的夹角,将 ∥u∥ 2 = 1 代入，并忽略与 u 无关的项，就能简化得到 minucosθ。

　　　　这在 u 与梯度方向相反时取得最小。换句话说，梯度向量指向上坡，负梯度向量指向下坡。

　　　　我们在负梯度方向上移动可以减小 f。这被称为最速下降法(method of steepest descent) 或梯度下降（gradient descent）

　　　　最速下降建议新的点为

　　　　　　

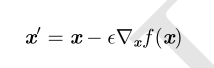
　　　　其中 ϵ 为学习率（learning rate），是一个确定步长大小的正标。

3.Jacobian（Jacobian）矩阵

　　如果我们有一个函数：f : R m → R n ，f 的 Jacobian 矩阵 J ∈ R n×m 定义

　　　　

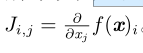
4.Hessian（Hessian）矩阵

　　

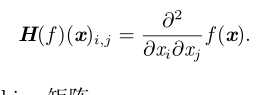
5.最优步长

　　

　　　　

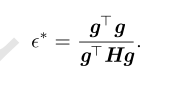
　　当 f ′ (x) = 0 且 f ′′ (x) > 0 时，x 是一个局部极小点。同样，当 f ′ (x) = 0 且 f ′′ (x) < 0 时，x 是一个局部极大点

　　当 f ′′ (x) = 0 时测试是不确定的。在这种情况下，x 可以是一个鞍点或平坦区域的一部分