常用概率分布

1.Bernoulli 分布（Bernoulli distribution）

　　单个二值随机变量的分布

　　它由单个参数 ϕ ∈ [0,1] 控制，ϕ 给出了随机变量等于 1 的概率

　　　　

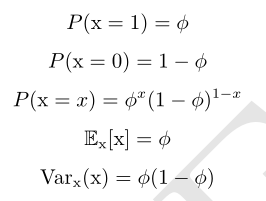
2.Multinoulli 分布

　　具有k个不同状态的单个离散随机变量上的分布

　　经常用来表示对象分类的分布

3.高斯分布

　　也是正态分布（normal distribution）

　　　　

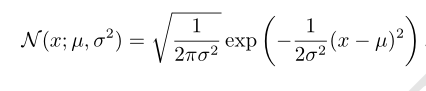
　　　　分布的均值：E[x] = µ，分布的标准差用 σ 表示，方差用 σ 2 表示

　　标准正态分布（standard normal distribution）

　　　　 µ = 0,σ = 1

　　　　

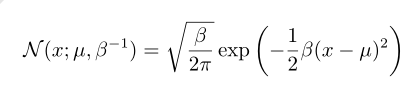
　　　　参数 β ∈ (0,∞)

　　建模的很多分布的真实情况是比较接近正态分布的

　　中心极限定理（central limit theorem）说明很多独立随机变量的和近似服从正态分布

　　在具有相同方差的所有可能的概率分布中，正态分布在实数上具有最大的不确定性

　　正态分布可以推广到 R n 空间，这种情况下被称为多维正态分布（multivariate normal distribution）

　　　　

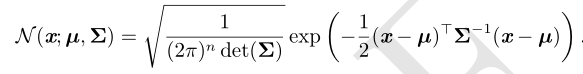
　　　　Σ参数是一个正定对称矩阵 ，参数 Σ 给出了分布的协方差矩阵

　　　　参数 µ 仍然表示分布的均值，只不过现在是向量值

　　　　

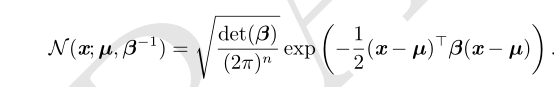
　　　　　　精度矩阵（precision matrix）β 进行替代Σ

　　　　　　常常把协方差矩阵固定成一个对角阵

　　　　　　各向同性（isotropic）高斯分布，它的协方差矩阵是一个标量乘以单位阵

4.指数分布和 Laplace 分布

　　指数分布（exponential distribution）

　　　　

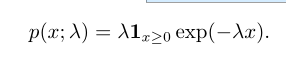
　　Laplace 分布（Laplace distribution）

　　　　

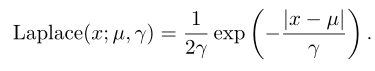
5.分布的混合