概率基本概念
1.随机变量(random variable)
可以随机地取不同值的变量。
通常用无格式字体 (plain typeface) 中的小写字母来表示随机变量本身,而用手写体中的小写字母来表示随机变量能够取到的值。
随机变量可以是离散的或者连续的。
2.概率分布
描述随机变量或一簇随机变量在每一个可能取到的状态的可能性大小
3.离散型变量和概率质量函数
离散型变量的概率分布可以用概率质量函数(probability mass function, PMF)来描述。
用大写字母 P 来表示概率质量函数
根据随机变量来推断所使用的 PMF,而不是根据函数的名称来推断;例如,P(x) 通常和 P(y) 不一样
概率质量函数将随机变量能够取得的每个状态映射到随机变量取得该状态的概率
P(x = x)
∼ 符号来说明它遵循的分布:x ∼ P(x)
4.联合概率分布(joint probability distribution)
概率质量函数可以同时作用于多个随机变量。
P(x = x,y = y) 表示 x = x 和y = y 同时发生的概率。我们也可以简写为 P(x,y)
PMF,必须满足下面这几个条件:
P 的定义域必须是 x 所有可能状态的集合
∀x ∈ x,0 ≤ P(x) ≤ 1. 不可能发生的事件概率为 0,并且不存在比这概率更低的状态。类似的,能够确保一定发生的事件概率为 1,而且不存在比这概率更高的状态。
∑x∈x P(x) = 1. 我们把这条性质称之为归一化的(normalized)
均匀分布(uniform distribution)的(也就是将它的每个状态视为等可能的)
5.连续型变量和概率密度函数
概率密度函数(probability density function, PDF)
连续型随机变量
条件:

概率密度函数 p(x) 并没有直接对特定的状态给出概率,相对的,它给出了落在面积为 δx 的无限小的区域内的概率为 p(x)δx
均匀分布
x ∼ U(a,b) 表示 x 在 [a,b] 上是均匀分布的
u(x;a,b)其中 a 和 b 是区间的端点且满足 b > a,符号“;’’ 表示 ‘‘以什么为参数’’;我们把 x 作为函数的自变量,a 和 b 作为定义函数的参数
6.边缘概率
一组变量的联合概率分布,其中一个子集的概率分布。这种定义在子集上的概率分布被称为边缘概率分布(marginal probability distribution)
依据下面的求和法则(sum rule)来计算 P(x):
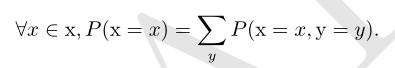
对于连续型变量,我们需要用积分替代求和:
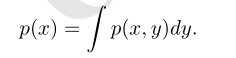


 浙公网安备 33010602011771号
浙公网安备 33010602011771号