数据结构快速回顾——平衡二叉树 AVL （转）

　　平衡二叉树（Balanced Binary Tree）是二叉查找树的一个进化体，也是第一个引入平衡概念的二叉树。1962年，G.M. Adelson-Velsky 和 E.M. Landis发明了这棵树，所以它又叫AVL树。平衡二叉树要求对于每一个节点来说，它的左右子树的高度之差不能超过1，如果插入或者删除一个节点使得高度之差大于1，就要进行节点之间的旋转，将二叉树重新维持在一个平衡状态。这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

　　平衡二叉树实现的大部分过程和二叉查找树是一样的（学平衡二叉树之前一定要会二叉查找树），区别就在于插入和删除之后要写一个旋转算法去维持平衡，维持平衡需要借助一个节点高度的属性。我参考了机械工业出版社的《数据结构与算法分析-C语言描述》写了一个C++版的代码。这本书的AVLTree讲的很好，不过没有很完整的去描述。我会一步一步的讲解如何写平衡二叉树，重点是平衡二叉树的核心部分，也就是旋转算法。

第一步：节点信息

　　相对于二叉查找树的节点来说，我们需要用一个属性二叉树的高度，目的是维护插入和删除过程中的旋转算法。

代码如下：

 

//AVL树节点信息

class tnode
{
    public:
    int val;
    int hgt;
    int freq;
    tnode* pleft;
    tnode* pright;
    tnode(int v):val(v),hgt(0),freq(1),pleft(NULL),pright(NULL){};
    tnode():val(0x7fffffff),hgt(0),freq(1),pleft(NULL),pright(NULL){};

};

 

第二步：声明头结点

tnode *head;

 

第三步：两个辅助方法

　　旋转算法需要借助于两个功能的辅助，一个是求树的高度，一个是求两个高度的最大值。这里规定，一棵空树的高度为-1，只有一个根节点的树的高度为0，以后每多一层高度加1。为了解决指针NULL这种情况，写了一个求高度的函数，这个函数还是很有必要的。

代码如下：

 

//计算以节点为根的树的高度

int height(tnode *t)
{
    if(t)
        return t->hgt;
    else
        return -1;
}

 

第四步：旋转

　　对于一个平衡的节点，由于任意节点最多有两个儿子，因此高度不平衡时，此节点的两颗子树的高度差2.容易看出，这种不平衡出现在下面四种情况：

　　1、6节点的左子树3节点高度比右子树7节点大2，左子树3节点的左子树1节点高度大于右子树4节点，这种情况成为左左。

　　2、6节点的左子树2节点高度比右子树7节点大2，左子树2节点的左子树1节点高度小于右子树4节点，这种情况成为左右。

　　3、2节点的左子树1节点高度比右子树5节点小2，右子树5节点的左子树3节点高度大于右子树6节点，这种情况成为右左。

　　4、2节点的左子树1节点高度比右子树4节点小2，右子树4节点的左子树3节点高度小于右子树6节点，这种情况成为右右。

　　从图2中可以可以看出，1和4两种情况是对称的，这两种情况的旋转算法是一致的，只需要经过一次旋转就可以达到目标，我们称之为单旋转。2和3两种情况也是对称的，这两种情况的旋转算法也是一致的，需要进行两次旋转，我们称之为双旋转。

第五步：单旋转

　　单旋转是针对于左左和右右这两种情况的解决方案，这两种情况是对称的，只要解决了左左这种情况，右右就很好办了。图3是左左情况的解决方案，节点k2不满足平衡特性，因为它的左子树k1比右子树Z深2层，而且k1子树中，更深的一层的是k1的左子树X子树，所以属于左左情况。

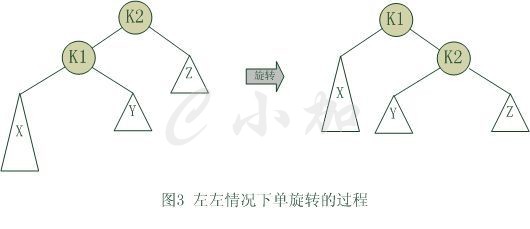
　　为使树恢复平衡，我们把k2变成这棵树的根节点，因为k2大于k1，把k2置于k1的右子树上，而原本在k1右子树的Y大于k1，小于k2，就把Y置于k2的左子树上，这样既满足了二叉查找树的性质，又满足了平衡二叉树的性质。

　　这样的操作只需要一部分指针改变，结果我们得到另外一颗二叉查找树，它是一棵AVL树，因为X向上一移动了一层，Y还停留在原来的层面上，Z向下移动了一层。整棵树的新高度和之前没有在左子树上插入的高度相同，插入操作使得X高度长高了。因此，由于这颗子树高度没有变化，所以通往根节点的路径就不需要继续旋转了。

代码如下：

 

 1 //左左旋转 
 2 void LLRotate(tnode *&tree)
 3 {
 4     tnode *tmp;
 5     tmp = tree->pleft;
 6     tree->pleft = tmp->pright;
 7     tmp->pright = tree;
 8     
 9     tree->hgt=max(height(tree->pleft),height(tree->pright))+1;
10     tmp->hgt= max(height(tmp->pleft),tree->hgt)+1;
11     //
12     tree = tmp;
13 }
14 
15 //右右旋转 
16 void RRRotate(tnode *&tree)
17 {
18     tnode *tmp;
19     tmp = tree->pright;
20     tree->pright=tmp->pleft;
21     tmp->pleft=tree;
22     
23     tree->hgt=max(height(tree->pleft),height(tree->pright))+1;
24     tmp->hgt= max(height(tmp->pleft),tree->hgt)+1;
25     
26     tree = tmp;
27 }

 

第六步：双旋转

　　对于左右和右左这两种情况，单旋转不能使它达到一个平衡状态，要经过两次旋转。双旋转是针对于这两种情况的解决方案，同样的，这样两种情况也是对称的，只要解决了左右这种情况，右左就很好办了。图4是左右情况的解决方案，节点k3不满足平衡特性，因为它的左子树k1比右子树Z深2层，而且k1子树中，更深的一层的是k1的右子树k2子树，所以属于左右情况。

 　　为使树恢复平衡，我们需要进行两步，第一步，把k1作为根，进行一次右右旋转，旋转之后就变成了左左情况，所以第二步再进行一次左左旋转，最后得到了一棵以k2为根的平衡二叉树树。

代码如下：

 

//左右旋转 
void LRRotate(tnode *&tree)
{
    RRRotate(tree->pleft);
    LLRotate(tree);
}

//右左旋转 
void RLRotate(tnode *&tree)
{
    LLRotate(tree->pright);
    RRRotate(tree); 
}

 

 第七步：插入

　　插入的方法和二叉查找树基本一样，区别是，插入完成后需要从插入的节点开始维护一个到根节点的路径，每经过一个节点都要维持树的平衡。维持树的平衡要根据高度差的特点选择不同的旋转算法。

代码如下：

 

//插入

void insert(tnode *&tree,int v)
{
    if(tree == NULL)
    {
        tree = new tnode(v);
        return;
    }    
    if(tree->val > v)
    {
        insert(tree->pleft,v);
        if(2 == height(tree->pleft)-height(tree->pright))
        {
            if(v<tree->pleft->val)
                LLRotate(tree);
            else
                LRRotate(tree);
        }
    }
    else if(tree->val < v)
    {
        insert(tree->pright,v);
        if( 2 == height(tree->pright)-height(tree->pleft))
        {
            if(v > tree->pright->val)
                RRRotate(tree);
            else
                RLRotate(tree);
        }
    }
    else
        (tree->freq)++;
    
    tree->hgt = max(height(tree->pleft),height(tree->pright))+1;
}

 

 

 

 

第八步：中序遍历

代码如下：

 

//中序遍历函数

void inOrder(tnode *tree)
{
    if(tree == NULL)return;
    inOrder(tree->pleft);
//    printf("%d\t",tree->val);
    printf("num:%d\thgt:%d\t",tree->val,tree->hgt);
    inOrder(tree->pright);
}

 

第十一步：关于效率

　　此数据结构插入、查找和删除的时间复杂度均为O(logN)，但是插入和删除需要额外的旋转算法需要的时间，有时旋转过多也会影响效率。

　　关于递归和非递归。我用的是递归的方法进行插入，查找和删除，而非递归的方法一般来说要比递归的方法快很多，但是我感觉非递归的方法写出来会比较困难，所以我还是选择了递归的方法。

　　还有一种效率的问题是关于高度信息的存储，由于我们需要的仅仅是高度的差，不需要知道这棵树的高度，所以只需要使用两个二进制位就可以表示这个差。这样可以避免平衡因子的重复计算，可以稍微的加快一些速度，不过代码也丧失了相对简明性和清晰度。如果采用递归写法的话，这种微加速就更显得微乎其微了。

 

 由于原文在左旋右旋函数中忘记更新父类节点的指向、插入函数中节点高度的计算忘记+1；本文对其内容介绍摘抄过来，但是修正了相应的函数。

摘自：http://www.cppblog.com/cxiaojia/archive/2014/03/02/187776.html