浅谈三分算法
前置知识：
二分，函数（数学领域）。
二分
首先二分的能解决的，仅仅是 单调函数 求极值。什么叫做单调函数？即 \(y\) 随 \(x\) 单调不减 或 单调不增 均可用二分解决。如图：
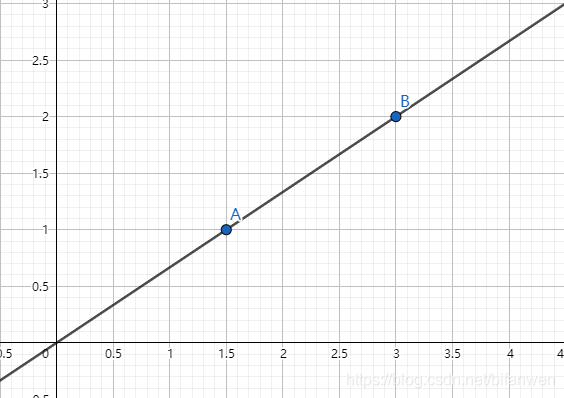
上图是函数 \(y=\frac{2}{3} x\)，显然可以用二分在函数上进行解决问题。
实际上二分的解决领域仅仅是 \(y=kx\) 类型的函数，二次及以上都不行了，反比例函数也不行了。
三分
辟谣
请不要以为我在开玩笑！确实有这样一个算法。
很多初学者会这样认为：
二分就是在 \([l,r]\) 找到中点 \(\text{mid} = \lfloor \frac{l+r}{2} \rfloor\)，把搜索范围每次减小一半。
三分就是在 \([l,r]\) 找到三等分点 \(\text{m1} = \lfloor \frac{l+r}{3} \rfloor , \text{m2} = \lfloor \frac{2(l+r)}{3} \rfloor\)，把搜索范围每次变为 \(\frac{1}{3}\)。
时间复杂度都是 \(\log\) 级别的（只不过 \(\log_2\) 和 \(\log_3\)），没有什么意义。
按照这个方法，我可以写出 \(k\) 分，写出 \(\log_k\)，不过复杂度还是 \(\log\)，都一样的，好难写！
三分不是你所谓的三分，它有一定的字面意思，但绝对不是这个意思！
二分和三分
首先我们来看一个函数：
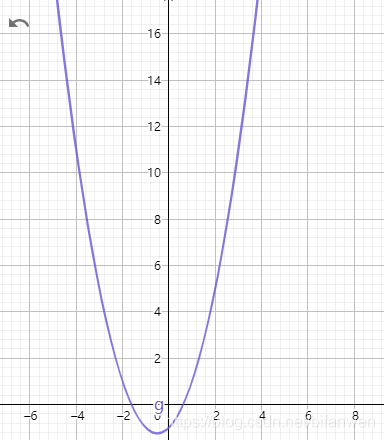
如图为 \(y = x^2 + x - 1\) 的二次函数，取名为 \(g\).
一个问题：\(x \in [-5 , 5]\) 时 \(y\) 的最小值为？（经典的单谷函数求最小值题）
假设我们二分，看是否能得到结果？能算下去吗？
第一步，\(l=-5 , r = 5 , \text{mid} = 0\)，则 \(g(\text{mid}) = -1\).
此时你怎么操作呢？是 \(l \gets \text{mid}\) 还是 \(r \gets \text{mid}\) 呢？
你不知道你取到的中点是在答案左边还是在答案右边，这样你肯定求不出来了。
所以，这时，我们要开始了解三分了！
三分的实现
对于 \([l,r]\)，首先找到 \(m1\) 和 \(m2\)（两个三等分点），把 \(g(m1)\) 和 \(g(m2)\) 进行比较。
当求的是最小值时：\(g(m1) < g(m2)\)，则 \(r=m2\)；否则 \(l=m1\).
当求的是最大值时：\(g(m1) > g(m2)\)，则 \(r=m2\)；否则 \(l=m1\).
如何理解呢？总之就是 离答案越近的就保留，离答案相对远的则作为下一次三分的端点。
还是那个题目：
求 \(y = x^2 + x -1\)，\(x \in [-5,5]\) 时的 \(\min(y)\).
手算一下：
可得 $x = - \frac{1}{2} 时 \(y\) 取到最小值为 \(- \frac{5}{4}\).
这个结果将用于检验我们的三分过程。（这里三分保留 \(2\) 位小数方便手算）
第一步 \(m1 = -1.67 , m2 = 1.67\)，你发现 \(m1\) 更接近，于是 \(l = -5 , r = 1.67\).
第二步 \(m1 = -2.77 , m2 = -0.55\)，你发现 \(m2\) 更接近，于是 \(l = -2.77 , r = 1.67\).
第三步 \(m1 = -1.29 , m2 = 0.19\)，你发现 \(\cdots \cdots\)
贴一下程序计算的结果：（每次输出 \(l,r\) 的值）
/*
程序保留了 11 位小数的精度，本题只需要 6 位精度
-5 5
-5 1.66667
-2.77778 1.66667
-1.2963 1.66667
-1.2963 0.679012
-1.2963 0.0205761
-0.857339 0.0205761
-0.857339 -0.272062
-0.662247 -0.272062
-0.662247 -0.402124
-0.575539 -0.402124
-0.575539 -0.459929
-0.537002 -0.459929
-0.537002 -0.48562
-0.519875 -0.48562
-0.508456 -0.48562
-0.508456 -0.493232
-0.503382 -0.493232
-0.503382 -0.496615
-0.503382 -0.498871
-0.501878 -0.498871
-0.500876 -0.498871
-0.500876 -0.499539
-0.50043 -0.499539
-0.50043 -0.499836
-0.500232 -0.499836
-0.5001 -0.499836
-0.5001 -0.499924
-0.500041 -0.499924
-0.500041 -0.499963
-0.500015 -0.499963
-0.500015 -0.499981
-0.500015 -0.499992
-0.500008 -0.499992
-0.500008 -0.499997
-0.500004 -0.499997
-0.500002 -0.499997
-0.500002 -0.499999
-0.500001 -0.499999
-0.500001 -0.5
-0.5 -0.5
*/
最后得到 \(x = - \frac{1}{2}\) 为最小值，计算即可。
是不是很妙？
代码实现
这里有一些细节。
你不能直接写 l = r，那样你肯定会因为奇怪的精度问题而陷入死循环。
所以，我们应当设置一个极小的常数为 \(s\)，\(l+s \geq r\) 即认为 \(l=r\)，可以用 \(s\) 的精度来调整三分的精度。 本题 \(s = 10^{-11}\) 已足够。当然只要在计算机能承受的精度之内 就没有问题（最多 \(10^{-14}\) ~ \(10^{-16}\)）了。
关于设置极小值的问题，越小越好，只要不超过计算机能承受的范围（不是指 \(\text{string}\) 的范围啊）即可，一般 -0x7fffffff 是简单粗暴的操作。当然 -1e16 也是可以的。总之不要因为最小值耽误了整个程序的正误啊！
最后贴一个模板（伪代码）：
while(l + (1e-11) < r) { //这里写的是单谷函数求最小值
lmid = l + (r-l) / 3;
rmid = r - (r-l) / 3;
if(calc(lmid) <= calc(rmid)) r = rmid;
else l = lmid;
}
/* */
while(l + (1e-11) < r) { //这里写的是单峰函数求最大值
lmid = l + (r-l) / 3;
rmid = r - (r-l) / 3;
if(calc(lmid) >= calc(rmid)) r = rmid;
else l = lmid;
}
掌握了模板，可以去写一些板子题啦！
