浅谈 Dancing Links X 算法
前置知识:
- 一维链表。(单向,双向,循环)
- 部分集合运算,如 \(\bigcap\),\(\bigcup\).
前言
在计算机科学中,X算法可用来求解精确覆盖问题。
精确覆盖问题 是哪一类问题呢? \(X\) 算法又是什么高深的算法呢?
背景
- 你的同学通过某种算法迅速 \(\text{AC}\) 了 P1784 数独,然后他兴致勃勃地 带领学生 \(1s\) 搞定数独竞赛 。
小时候,你玩数独;长大了,数独玩你。你该怎么办?
- 那位同学用 \(\text{DLX}\) 轻松码力全开搞定了 P4205 『NOI2005』智慧珠游戏
小时候,你玩智慧珠;长大了,智慧珠玩你。你该怎么办?
定义
\(\text{Dancing Links X}\) 是优化后的 \(X\) 算法,用于解决 精确覆盖问题。
精确覆盖问题 是这样一类问题:给定若干集合 \(S_1 , S_2 \cdots S_n\) 和一个集合 \(X\),求出 \(T1 , T2 \cdots T_k\) 使得满足:
翻译成人话 其实就是在 \(n\) 个集合中选出若干 两两不相交 的集合且 这些集合的并为 \(X\).
比方说:
那么这时答案就应该是取 \(S_4\) 和 \(S_3\).
那么,如何解决这类问题呢?
算法一
暴力搜索解决问题。
我们用 \(2^n\) 的时间枚举每个集合是否被选择。然后 \(O(n)\) 验证即可。
时间复杂度:\(O(2^n \times nm)\).(\(m\) 为 \(\bigcup_{i=1}^n S_i\) 的大小)
算法二
不得不说算法一时间无法承受。
我们首先将 \(S\) 与 \(X\) 离散化,并构造矩阵 \(a (n \times m)\) ,其中 \(a_{i,j}\) 表示 \(S_i\) 是否含有离散化后的 \(j\);\(m\) 为 \(\bigcup_{i=1}^n S_i\) 的大小。
那么,对上述问题建矩阵可得:
其中 \(1\) ~ \(6\) 列分别表示:\(\in 666 , \in 2 , \in 8 , \in 4 , \in 5 , \in 119\).
问题转化为:求 \(01\) 矩阵选出若干行,使得每列 有且只有 \(1\) 个 \(1\).
考虑将每行看做一个二进制数,即要求所有选出行的 或 为 \(2^m-1\),且任意两个数的 与 为 \(0\).
用一个变量记录当前或值,然后计算即可。
时间复杂度:\(O(2^n \times n)\).
算法三
考虑 \(X\) 算法。回顾一下这个图:
首先我们选择第一行,然后把第一行的 \(1\) 所在列标记,把所有 被标记的列上有 \(1\) 的那一行删除。 得到:
绿色表示标记的列,红色表示当前行,紫色表示被删除的行。
为什么呢?因为 当前列有了 \(1\),别的列不能再有了;有的肯定不能选,删除它们是一个有力的剪枝。
然后你发现你只能选第 \(3\) 行,验证后发现第 \(6\) 列没有 \(1\),所以回溯,不选第 \(1\) 行。回溯之前,需要 恢复之前删掉的行 。
注:图上 \(a_{2,2}\) 忘记标了,不过第 \(1\) 行不在我们考虑的范围内(已经确定不能选了),不会影响结果;但忘记标了可能会影响理解,大家谅解一下。
当然,这里如果为了方便理解把第一行删去也是可以的。
然后同理,你发现第 \(2\) 行选了之后无行可选。(因为前面的搜索已经确定了第 \(1\) 行选了无解,所以不选)
验证,发现第 \(1\) 列没有选 \(1\) (后面的不用再看,一列无解就是无解了),直接回溯,说明第 \(2\) 行也不能选,恢复删除行。
然后选第 \(3\) 行。
咦?你发现可以递归下去选第 \(4\) 行。
验证发现正确!
所以得到答案:\(S_3 , S_4\),退出搜索。
所以,\(X\) 算法的步骤大致为:
-
对当前矩阵删除当前行,并删去与当前行有公共元素(即同列有 \(1\)) 的所有行,递归下一层。
-
如果所有行返回无解即返回无解给上一层,并恢复行,回到第 \(1\) 步。
-
如果发现所有列都被标记则输出答案,结束搜索。
-
所有搜索无解则返回无解。
你发现,该搜索需要大量的 删除行,恢复行 的操作。
而 \(X\) 算法的时间复杂度是 指数级 的,其回溯、搜索层数取决于 矩阵中 \(1\) 的个数 而不是 \(n\) 或者 \(m\) 的大小。其时间复杂度大概可以接受 \(n,m \leq 100\) 的情况。
算法四
\(\text{Dancing Links 意为:跳舞的链}\)
为什么叫做 跳舞的链 呢?是这样的。
假设我们要写这样一道题目:
给定一个 \(n \times m\) 的二维矩阵,你需要支持 \(q\) 个操作:
- 删除 第 \(x\) 行 ;
- 查询 \(a_{i,j}\) 的值。
数据范围:\(n,m \leq 500\),\(q \leq 10^5\).
当然如果你暴力删除的话,时间复杂度是 \(O(n \cdot m \cdot q)\).
但是我们想一个弱化版:
给定一个长为 \(n\) 的数组,你需要支持 \(q\) 个操作:
- 删除第 \(x\) 个数;
- 查询第 \(a_i\) 的值。
数据范围:\(n \leq 500\),\(q \leq 10^5\).
这直接用一维链表弄一下就可以了是不?
所以,一个叫 \(\texttt{Donald E. Knuth}\) 的计算机科学家,发明了 “十字链表” 解决此类问题。
十字链表的图大概是这样的:
(下面十字链表的图,代码思路摘自 DLX 详细讲解)
似乎非常简单的样子,那再给一张:
说白了你第一眼看到我也是这个感觉:

别扯了,说正题。回到这个图:
每个节点弄个指针指向它上下左右的节点,然后再开数组记录每行,每列的元素个数。 \(fir_i\) 是我们在每行链表之前虚构的一个元素,每次从它开始遍历。
STEP 1
#define FOR(i,A,x) for(int i=A[x];i!=x;i=A[i])
预处理优化宏定义都好用
定义数组。
int n,m,id,fir[N],siz[N];
int L[N],R[N],U[N],D[N];
int col[N],row[N],ans;
int stk[N]; //stk 记录答案
STEP 2
如何建立一个 \(n \times m\) 的 \(\text{Dancing Link?}\) 很显然,对于一行是这样的:
inline void build(int x,int y) {
// printf("build : %d %d\n",x,y);
n=x,m=y; for(int i=0;i<=y;i++)
L[i]=i-1,R[i]=i+1,U[i]=D[i]=i; //左右是 i-1,i+1 , 上下就是自己
L[0]=y,R[y]=0,id=y;
memset(fir,0,sizeof(fir));
memset(siz,0,sizeof(siz));
}
那你会说,嗯,不对呀?这样我们只是初始化一行而已?
对,所以我们对每个集合插入节点,通过插入来实现。

如果 \(\text{idx}\) 的位置已经有了,那么把它插入到已有的下面去,这样 同列的 \(1\) 就会被放在不同行 了;否则已经有的话就直接按照链表思路插入。插入顺序要记清!
inline void insert(int x,int y) {
// printf("insert : %d %d\n",x,y);
col[++id]=y,row[id]=x,++siz[y]; //记录个数,插入
// U[id]=D[id]=y,U[D[y]]=id,D[y]=id;
D[id]=D[y],U[D[y]]=id,U[id]=y,D[y]=id; //维护上下
if(!fir[x]) fir[x]=L[id]=R[id]=id; //没出现则自己作为第一个
else R[id]=R[fir[x]],L[R[fir[x]]]=id,L[id]=fir[x],R[fir[x]]=id; //接在第一个后面
}
早警告过你今天前置知识是链表,看你不会链表一个也写不了了
STEP 3
那么如何删除一行呢?
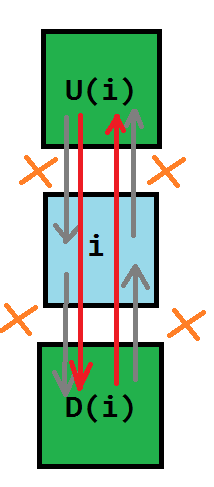
嗯,上下互相指,然后每列个数减。是不是很简单?
inline void remove(int x) {
// printf("remove : %d\n",x);
L[R[x]]=L[x]; R[L[x]]=R[x];
FOR(i,D,x) FOR(j,R,i) U[D[j]]=U[j],D[U[j]]=D[j],--siz[col[j]];
}
那么同理考虑删除列:
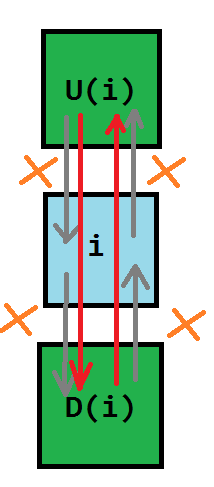
inline void recover(int x) {
// printf("recover : %d\n",x);
FOR(i,U,x) FOR(j,L,i) U[D[j]]=D[U[j]]=j,++siz[col[j]];
L[R[x]]=R[L[x]]=x;
}
算法五
回忆一下 \(X\) 算法的过程:
-
对当前矩阵删除当前行,并删去与当前行有公共元素(即同列有 \(1\)) 的所有行,递归下一层。
-
如果所有行返回无解即返回无解给上一层,并恢复行,回到第 \(1\) 步。
-
如果发现所有列都被标记则输出答案,结束搜索。
-
所有搜索无解则返回无解。
加个剪枝: 选择列元素最少的删除,这个剪枝太显然了吧。因为元素少的更容易被决定。
你发现 删除行,列 可以直接用上面的十字链表维护。
我们要开始写最重要的 \(\text{dance}\) 啦! 其实十字链表真的很想跳舞的,不然不会叫这么名字的。
强烈建议读者返回亲自推一下那个图,不然代码实在理解不了。
inline bool dance(int dep) {
// printf("dance : %d\n",dep);
if(!R[0]) {ans=dep;return 1;} //0 号没有右边元素 , 即整列都被标记,说明有答案
int wz=R[0]; FOR(i,R,0) if(siz[i]<siz[wz]) wz=i; // 找到最小的那个
remove(wz); FOR(i,D,wz) { //删除
stk[dep]=row[i]; FOR(j,R,i) remove(col[j]); //标记的全部删除
if(dance(dep+1)) return 1; //往下走
FOR(j,L,i) recover(col[j]); //恢复
} recover(wz); return 0; //恢复 , 返回无解
}
嗯,好了,大家只要弄明白每部分的意思,我们就来看题吧!
时间复杂度:\(O(c^n)\). 是指数级的,\(n\) 是矩阵 \(1\) 的个数,\(c\) 是某个很接近 \(1\) (\(>1\)) 的常数。但一般而言不会出现卡 \(\text{Dancing Links X}\) 的出题人吧。
实际得分:\(100pts\).
#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+1;
#define FOR(i,A,x) for(int i=A[x];i!=x;i=A[i])
inline int read(){char ch=getchar();int f=1;while(ch<'0' || ch>'9') {if(ch=='-') f=-f; ch=getchar();}
int x=0;while(ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;}
int n,m,id,fir[N],siz[N];
int L[N],R[N],U[N],D[N];
int col[N],row[N],ans;
int stk[N];
inline void remove(int x) {
// printf("remove : %d\n",x);
L[R[x]]=L[x]; R[L[x]]=R[x];
FOR(i,D,x) FOR(j,R,i) U[D[j]]=U[j],D[U[j]]=D[j],--siz[col[j]];
}
inline void recover(int x) {
// printf("recover : %d\n",x);
FOR(i,U,x) FOR(j,L,i) U[D[j]]=D[U[j]]=j,++siz[col[j]];
L[R[x]]=R[L[x]]=x;
}
inline void build(int x,int y) {
// printf("build : %d %d\n",x,y);
n=x,m=y; for(int i=0;i<=y;i++)
L[i]=i-1,R[i]=i+1,U[i]=D[i]=i;
L[0]=y,R[y]=0,id=y;
memset(fir,0,sizeof(fir));
memset(siz,0,sizeof(siz));
}
inline void insert(int x,int y) {
// printf("insert : %d %d\n",x,y);
col[++id]=y,row[id]=x,++siz[y];
// U[id]=D[id]=y,U[D[y]]=id,D[y]=id;
D[id]=D[y],U[D[y]]=id,U[id]=y,D[y]=id;
if(!fir[x]) fir[x]=L[id]=R[id]=id;
else R[id]=R[fir[x]],L[R[fir[x]]]=id,L[id]=fir[x],R[fir[x]]=id;
}
inline bool dance(int dep) {
// printf("dance : %d\n",dep);
if(!R[0]) {ans=dep;return 1;}
int wz=R[0]; FOR(i,R,0) if(siz[i]<siz[wz]) wz=i;
remove(wz); FOR(i,D,wz) {
stk[dep]=row[i]; FOR(j,R,i) remove(col[j]);
if(dance(dep+1)) return 1;
FOR(j,L,i) recover(col[j]);
} recover(wz); return 0;
}
int main(){
n=read(),m=read(); build(n,m);
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)
if(read()) insert(i,j);
dance(1);
if(ans) for(int i=1;i<ans;i++) printf("%d ",stk[i]);
else puts("No Solution!");
return 0;
}
嗯,博主之后会更数独的解法,还有智慧珠。不过现在这儿咕一会儿吧。
利用精确覆盖解决问题!
有了 DLX 解决精确覆盖,我们 1s AK 数独不是梦想!




