P2341 [USACO03FALL][HAOI2006]受欢迎的牛 G 题解
简要题意:
给定一张图,求多少个点,每个点都能到达它。
本题作为强连通分量的入门题。
何为强连通分量?有什么用?
下面一一解释。
首先,我们要确认,这道题目如果不用强连通分量而用其它方法(比如说暴力)的话:
时间复杂度将达到 \(O(n^2)\),此时不易通过,也非正解。
强连通分量是什么?我们来看一张图吧。
我们希望,如果能把环通过某种方式去掉,然后变成有向无环图,就很容易了。
一个强连通分量中的点两两可达。(有向图中)一个点也可以被认为是一个强连通分量。
也就是说,你会发现,一个环 或者 若干个相交的环 都会变成一个强连通分量。
显然它们两两可达,最后图会变成若干个强连通分量。

你会发现,\(1\) 是一个强连通分量,\(2,3,4,5\) 是一个强连通分量,\(6\),\(7\),\(8\) 均为一个单独的强连通分量。
此时我们可以简化这个图变成:
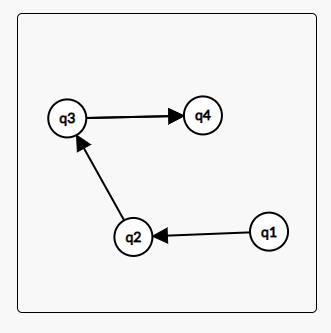
\(qx\) 表示 \(x\) 号强连通分量。
此时你发现 \(q4\) 就是答案,里面装的是 \(7\),所以答案为 \(1\).
那么问题在于,如何求强连通分量?
回到这个图。

用 \(dfn_i\) 表示 \(i\) 的遍历编号(就是我们常说的 “时间戳”),\(f_i\) 为 \(i\) 号节点属于的强连通分量编号,\(low_i\) 为 \(i\) 号节点能走到的 \(dfn\) 值最小的节点。
一开始 \(low_i = i (1 \leq i \leq n)\).
首先,我们从 \(1\) 节点开始遍历,走到 \(2\).
然后走到了 \(3,4,5\) ,没有问题。此时 \(dfn_i = i (1 \leq i \leq 5)\)
然后,\(5\) 走到 \(2\) ,说明什么?
说明出现了环,说明出现了一个强连通分量(不一定完整,也就是不一定是一个完整的强连通分量)!
此时,\(dfn_i = 2 (3 \leq i \leq 5)\),这是需要更新的。那么此时第一个强连通分量产生了:
\(low_i = 1 (2 \leq i \leq 5)\).
然后你回溯,发现 \(5\) 没有其它节点可走。因为它属于一个未确定的强连通分量,因此保留。
同样,回溯到 \(4\),继续到 \(3\),走到了 \(6\).
继续走到 \(7\). 此时 \(7\) 没有其它节点可走,并且 \(low_7 = 7\),说明 它只能走到自己,也不存在别人能走到它——因为它没有节点可走。所以它是一个单独的强连通分量,我们把它标记,即丢弃。
然后,回溯到 \(6\).发现 \(6\) 也没有其它节点可走(\(7\) 已经被标记丢弃了),所以同理,\(6\) 也是一个强连通分量,标记丢弃掉。
接着回溯到 \(3\),回溯到 \(2\).
然后 \(2\) 走到了 \(8\),发现 \(8\) 也没有其它节点可走(\(7\) 已经被标记丢弃了),所以同理,\(8\) 也是一个强连通分量,标记丢弃掉。
然后回溯到 \(2\),发现 \(2\) 没有可以走的节点了。所以,和 \(2\) 出于同一个强连通分量的节点全部被标记丢弃掉。
此时回溯到 \(1\),\(1\) 也作为了一个单独的强连通分量。
此时强连通分量就求出来了。
那么你会说,这些过程有一个难维护的细节:就是 “同一个强连通分量的节点全部被标记丢弃掉”,难道还要扫一遍吗?
不用。我们可以用栈维护。每走过一个节点进栈,标记丢弃则出栈。
inline void dfs(int u) {
dfn[u]=low[u]=++times;
s.push(u); h[u]=1;
for(int i=0,t;i<G[u].size();i++) {
t=G[u][i];
if(!dfn[t]) {
dfs(t); low[u]=min(low[u],low[t]); // 如果 t 能往上,那么 u 也能
} else if(h[t]) low[u]=min(low[u],dfn[t]); // 否则直接统计
}
if(low[u]==dfn[u]) { //表示当前节点无法向上,则统计答案
cnt++; int k;
do {
// a[cnt].push_back(s.top());
k=s.top();
h[k]=0; f[k]=cnt;
gs[cnt]++; s.pop();
} while(k!=u) ;
}
}
此时,重构的图(代码中未重构)
那么,如何维护最终的答案?
你会发现,如果按照强连通分量重新构图,则一定是 有向无环图 。(不一定是树,因为有可能是菱形状)
下面证明两个结论:
- 如果有 \(\geq 2\) 个点出度为 \(0\),则整张图不存在答案。
证明:
如果有 \(\geq 2\) 个点出度为 \(0\),则首先除了这 \(2\) 个点外的其它所有点都不会是答案。因为这 \(2\) 个点就无法到达它们。
然后,这两个点也不是答案。因为,它们互相无法到达,也就促使了互相都不是答案。得证。
- 如果只有 \(1\) 个点出度为 \(0\),则这个答案就是它。
证明:
首先 \(y\) 不连向其它任何点,所以,整张图的答案要么是它,要么不是它。
如果这个结论不成立的话,结合上面的结论,你会发现答案始终为 \(0\).
但是样例告诉我们,不是这样的。所以得证。
这个证明可能有点不太严谨,但是考场上这样证就足够了
但是我们不需要重构这个图。
因为,我们这需要在原图上查边 \(u \rightarrow v\),如果 \(f_u \not = f_v\),说明不属于同一个强连通分量,就 \(du_{f_u} \gets du_{f_u} + 1\),\(du_i\) 表示第 \(i\) 个强连通分量 缩点后 的出度。
另:把每个强连通分量看做一个点,这样的方法叫做缩点。
最后统计出度即可。
时间复杂度:\(O(n + m)\).
实际得分:\(100pts\).
#pragma GCC optimize(2)
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#include<stack> //由于 POJ 不支持万能头,因此要手写
using namespace std;
const int N=1e5+1;
inline int read(){char ch=getchar();int f=1;while(ch<'0' || ch>'9') {if(ch=='-') f=-f; ch=getchar();}
int x=0;while(ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;}
bool h[N]; int cnt=0;
int times,dfn[N],du[N];
int low[N],n,m,f[N],gs[N];
vector<int>G[N];
stack<int>s;
inline void dfs(int u) {
dfn[u]=low[u]=++times;
s.push(u); h[u]=1;
for(int i=0,t;i<G[u].size();i++) {
t=G[u][i];
if(!dfn[t]) {
dfs(t); low[u]=min(low[u],low[t]);
} else if(h[t]) low[u]=min(low[u],dfn[t]);
}
if(low[u]==dfn[u]) {
cnt++; int k;
do {
// a[cnt].push_back(s.top());
k=s.top();
h[k]=0; f[k]=cnt;
gs[cnt]++; s.pop();
} while(k!=u) ;
}
} //Tarjan 模板
int main(){
n=read(),m=read();
while(m--) {
int x=read(),y=read();
G[x].push_back(y);
} for(int i=1;i<=n;i++)
if(!dfn[i]) dfs(i);
for(int u=1;u<=n;u++)
for(int i=0;i<G[u].size();i++) {
int x=G[u][i];
if(f[u]-f[x]) du[f[u]]++;
}
// for(int i=1;i<=n;i++) printf("%d ",f[i]); putchar('\n');
// for(int i=1;i<=cnt;i++) printf("%d ",gs[i]); putchar('\n');
// for(int i=1;i<=n;i++) printf("%d ",du[i]); putchar('\n');
int ans=0;
for(int i=1;i<=cnt;i++)
if(!du[i]) {
if(ans) {puts("0");return 0;} //已经有入度为 0 的,再来一个,答案为 0,结束
ans=i; //记录入度为 0 强连通分量的编号
} printf("%d\n",gs[ans]); //强连通分量的大小即为答案
return 0;
}



