距离、相似和相关
下面对距离、相似和相关做一个总结。
目录:
1. 欧氏距离
2. 曼哈顿距离
3. 切比雪夫距离
4. 闵可夫斯基距离
5. 标准化欧氏距离
6. 马氏距离
7. 夹角余弦距离
8. 海明距离
9. Dice系数
10. 杰卡德距离、SMC、Tanimoto系数与minhash
11. Pearson相关系数
12. 信息熵与KL距离
13. bregman 散度距离
13. 关联
14. 贝叶斯
15. 卡方检验
16. slope one
17. svd与pca和F范数
18. sigmoid/tanh
19. simhash
20. bloomfilter
满足以下几种性质的量,可以成为度量(metric):
非负性
(a)d(x,y)>=0
(b)d(x,y)=0 if x==y
对称性
d(x,y) = d(y,x) for all x,y
三角性
d(x,z)<= d(x,y) + d(y,z)
metrics对于许多算法是必须的,不过很多情况下,不必满足metrics也可以作为距离度量。
1. 欧氏距离
欧氏距离是最易于理解的一种距离计算方法,源自欧氏空间中两点间的距离公式。公式为:

2. 曼哈顿距离
从名字就可以猜出这种距离的计算方法了。想象你在曼哈顿要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼。实 际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源, 曼哈顿距离也称为城市街区距离(City Block distance)。公式为:
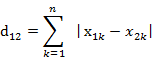
3. 切比雪夫距离
国际象棋玩过么?国王走一步能够移动到相邻的8个方格中的任意一个。那么国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?自己走走试试。你会发现最少步数总是 max( | x2-x1 | , | y2-y1 | ) 步。有一种类似的一种距离度量方法叫切比雪夫距离。公式为:

这个公式的另一种等价形式是

4. 闵可夫斯基距离
闵氏距离不是一种距离,而是一组距离的定义。公式为:

其中p是一个变参数。
当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离
当p→∞时,就是切比雪夫距离
根据变参数的不同,闵氏距离可以表示一类的距离。
闵氏距离的缺点:
闵氏距离,包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点。
简单说来,闵氏距离的缺点主要有两个:
(1)将各个分量的量纲(scale),也就是“单位”当作相同的看待了。
(2)没有考虑各个分量的分布(期望,方差等)可能是不同的。
5. 标准化欧氏距离
标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。标准欧氏距离的思路:既然数据各维分量的分布不一样,好吧!那我先将各个分量都“标准化”到均值、方差相 等吧。均值和方差标准化到多少呢?这里先复习点统计学知识吧,假设样本集X的均值(mean)为m,标准差(standard deviation)为s,那么X的“标准化变量”表示为:
而且标准化变量的数学期望为0,方差为1。因此样本集的标准化过程(standardization)用公式描述就是:
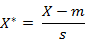
标准化后的值 = ( 标准化前的值 - 分量的均值 ) /分量的标准差
经过简单的推导就可以得到两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的标准化欧氏距离的公式:

如果将方差的倒数看成是一个权重,这个公式可以看成是一种加权欧氏距离(Weighted Euclidean distance)。
6. 马氏距离
(1)马氏距离定义
有M个样本向量X1~Xm,协方差矩阵记为S,均值记为向量μ,则其中样本向量X到u的马氏距离表示为:
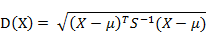
而其中向量Xi与Xj之间的马氏距离定义为:

若协方差矩阵是单位矩阵(各个样本向量之间独立同分布),则公式就成了:
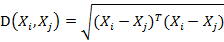
也就是欧氏距离了。
若协方差矩阵是对角矩阵,公式变成了标准化欧氏距离。
(2)马氏距离的优缺点:
量纲无关,排除变量之间的相关性的干扰。
7. 夹角距离
几何中夹角余弦可用来衡量两个向量方向的差异,机器学习中借用这一概念来衡量样本向量之间的差异。公式为
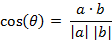
即:
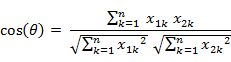
夹角余弦取值范围为[-1,1]。夹角余弦越大表示两个向量的夹角越小,夹角余弦越小表示两向量的夹角越大。当两个向量的方向重合时夹角余弦取最大值1,当两个向量的方向 完全相反夹角余弦取最小值-1。
8. 海明距离
两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。例如字符串“1111”与“1001”之间的汉明距离为2。
应用:信息编码(为了增强容错性,应使得编码间的最小汉明距离尽可能大)。
9. Dice 系数
10. 杰卡德距离、SMC与minhash
(1) 杰卡德相似系数
两个集合A和B的交集元素在A,B的并集中所占的比例,称为两个集合的杰卡德相似系数,用符号J(A,B)表示。
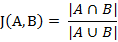
杰卡德相似系数是衡量两个集合的相似度一种指标。
(2) 杰卡德距离
与杰卡德相似系数相反的概念是杰卡德距离(Jaccard distance)。杰卡德距离可用如下公式表示:
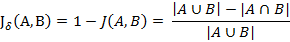
杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。
(3) 杰卡德相似系数与杰卡德距离的应用
可将杰卡德相似系数用在衡量样本的相似度上。
SMC
两个特征向量A,B,如果其值都是0,1的二值数据,那么有一个简单的判定相似性的方法:
F00 = A中为0并且B中也为0的个数
F10 = A1 B0的个数
F01 = A0 B1的个数
F11 = A1 B1 的个数
那么可以定义这么一个similarity:

这叫做(simplematch coefficient)SMC,简单匹配系数。
很多情况下,两个向量中,0的个数会大大多于1的个数,也就很稀疏,类不平衡。这时候不同向量之间的SMC会因为过多出现的0而没有效果。
那么我们可以只考虑F11,得到:

这也就是Jaccard距离。
广义Jaccard系数可以用于文档数据,并在二元属性情况下归约为Jaccard系数。广义Jaccard系数又称Tanimoto系数。
Minhash
MinHash也是LSH的一种,可以用来快速估算两个集合的相似度。MinHash由Andrei Broder提出,最初用于在搜索引擎中检测重复网页。它也可以应用于大规模聚类问题。
那么对集合A、B,hmin(A) = hmin(B)成立的条件是A ∪ B 中具有最小哈希值的元素也在 ∩ B中。这里
有一个假设,h(x)是一个良好的哈希函数,它具有很好的均匀性,能够把不同元素映射成不同的整数。
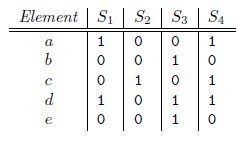
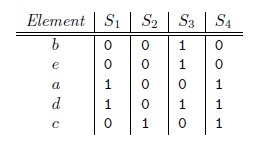
所以有,Pr[hmin(A) = hmin(B)] = J(A,B),即集合A和B的相似度为集合A、B经过hash后最小哈希值相等的概率。
11. Pearson相关系数
(1) 相关系数的定义
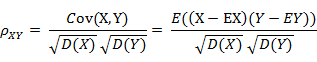
相关系数是衡量随机变量X与Y相关程度的一种方法,相关系数的取值范围是[-1,1]。相关系数的绝对值越大,则表明X与Y相关度越高。当X与Y线性相关时,相关系数取值为 1(正线性相关)或-1(负线性相关)。
(2)相关距离的定义
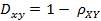
12. 信息熵与KL距离
信息熵是衡量分布的混乱程度或分散程度的一种度量。分布越分散(或者说分布越平均),信息熵就越大。分布越有序(或者说分布越集中),信息熵就越小。
计算给定的样本集X的信息熵的公式:
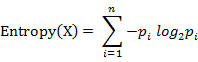
参数的含义:
n:样本集X的分类数
pi:X中第i类元素出现的概率
信息熵越大表明样本集S分类越分散,信息熵越小则表明样本集X分类越集中。当S中n个分类出现的概率一样大时(都是1/n),信息熵取最大值log2(n)。当X只有一个分类 时,信息熵取最小值0
KL距离,是Kullback-Leibler差异(Kullback-Leibler Divergence)的简称,也叫做相对熵(Relative Entropy)。它衡量的是相同事件空间里的两个概率分布的差异情 况。其 物理意义是:在相同事件空间里,概率分布P(x)的事件空间,若用概率分布Q(x)编码时,平均每个基本事件(符号)编码长度增加了多少比特。我们用 D(P||Q)表示KL距 离,计算公式如下:
![]()
当两个概率分布完全相同时,即P(x)=Q(X),其相对熵为0 。
D(P||Q)始终大于等于0的。虽然KL被称为距离,但是其不满足距离定义的三个条件:1)非负性;2)对称性(不满足);3)三角不等式(不满足)。
对一个信息源编码,按照其本身的概率分布进行编码,每个字符的平均比特数目最少。这就是信息熵的概念,衡量了信息源本身的不确定性。另外,可以看出KL距离不满足对称性,即D(P||Q)不一定等于D(Q||P)。
当然,我们也可以验证KL距离不满足三角不等式条件。
其实,KL距离在信息检索领域,以及统计自然语言方面有重要的运用。
13.bregman 散度距离
形式如下:

其中 为某个凸函数,
表示函数对y求导,<>表示点乘。
我们把y=x^2作为 ,得到:

即得到欧式距离。
Bregman距离的数学性质及推导不知,wiki上说,其为许多常见距离的一个通式。
wiki http://en.wikipedia.org/wiki/Bregman_divergence
其中包括欧式距离,曼哈顿距离,KL距离等等。
设I={i1,i2,..,im}是项集,其中ik(k=1,2,…,m)可以是购物篮中的物品,也可以是保险公司的顾客。设任务相关的数据D是事务集,其中每个事务T是项集,使得TÍI。设A是一个项集,且AÍT。
关联规则是如下形式的逻辑蕴涵:A Þ B,AÌI, AÌI,且A∩B=F。关联规则具有如下两个重要的属性:
支持度: P(A∪B),即A和B这两个项集在事务集D中同时出现的概率。
置信度: P(B|A),即在出现项集A的事务集D中,项集B也同时出现的概率。
同时满足最小支持度阈值和最小置信度阈值的规则称为强规则。给定一个事务集D,挖掘关联规则问题就是产生支持度和可信度分别大于用户给定的最小支持度和最小可信度的关联规则,也就是产生强规则的问题。
14. 贝叶斯
已知某条件概率,如何得到两个事件交换后的概率,也就是在已知P(A|B)的情况下如何求得P(B|A)。这里先解释什么是条件概率:
表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。其基本求解公式为:
。
贝叶斯定理之所以有用,是因为我们在生活中经常遇到这种情况:我们可以很容易直接得出P(A|B),P(B|A)则很难直接得出,但我们更关心P(B|A),贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。
下面不加证明地直接给出贝叶斯定理:
朴素贝叶斯分类的原理与流程:
朴素贝叶斯分类是一种十分简单的分类算法,叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素,朴素贝叶斯的思想基础是这样的:对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。通俗来说,就好比这么个道理,你在街上看到一个黑人,我问你你猜这哥们哪里来的,你十有八九猜非洲。为什么呢?因为黑人中非洲人的比率最高,当然人家也可能是美洲人或亚洲人,但在没有其它可用信息下,我们会选择条件概率最大的类别,这就是朴素贝叶斯的思想基础。
朴素贝叶斯分类的正式定义如下:
1、设为一个待分类项,而每个a为x的一个特征属性。
2、有类别集合。
3、计算。
4、如果,则
。
那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做:
1、找到一个已知分类的待分类项集合,这个集合叫做训练样本集。
2、统计得到在各类别下各个特征属性的条件概率估计。即
。
3、如果各个特征属性是条件独立的,则根据贝叶斯定理有如下推导:
因为分母对于所有类别为常数,因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的,所以有:
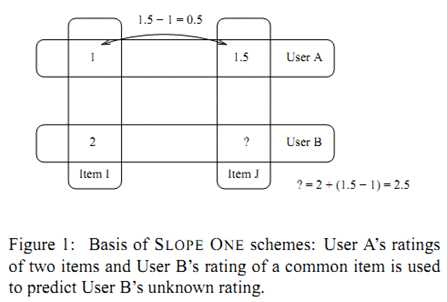
其基本的想法来自于简单的一元线性模型 w=f(v)=v+b。已知一组训练点 (vi,wi)ni=1,利用此线性模型最小化预测误差的平方和,我们可以获得
利用上式获得了b的取值后,对于新的数据点vnew,我们可以利用 wnew=b+vnew 获得它的预测值。
直观上我们可以把上面求偏移 b 的公式理解为 wi 和 vi 差值的平均值。
利用上面的直观,我们定义item i 相对于 item j 的平均偏差:
其中 Sj,i() 表示同时对item i 和 j 给予了评分的用户集合,而 card() 表示集合包含的元素数量。
有了上面的定义后,我们可以使用 ![]() 获得用户 u 对 item j 的预测值。当把所有这种可能的预测平均起来,可以得到:
获得用户 u 对 item j 的预测值。当把所有这种可能的预测平均起来,可以得到:
其中 Rj 表示所有用户 u 已经给予评分且满足条件 (i≠j 且 Sj,i非空) 的item集合。
对于足够稠密的数据集,我们可以使用近似
把上面的预测公式简化为
假设C是M x N矩阵,U是M x M矩阵,其中U的列为CCT的正交特征向量,V为N x N矩阵,其中V的列为CTC的正交特征向量,再假设r为C矩阵的秩,则存在奇异值分解:
Σ为M X N,其中![]()
![]() ,其余位置数值为0,
,其余位置数值为0,![]() 的值按大小降序排列。以下是Σ的完整数学定义:
的值按大小降序排列。以下是Σ的完整数学定义:
σi称为矩阵C的奇异值。
用C乘以其转置矩阵CT得:
奇异值分解的图形表示:
从图中可以看到Σ虽然为M x N矩阵,但从第N+1行到M行全为零,因此可以表示成N x N矩阵,又由于右式为矩阵相乘,因此U可以表示为M x N矩阵,VT可以表示为N x N矩阵
低阶近似
LSA潜在语义分析中,低阶近似是为了使用低维的矩阵来表示一个高维的矩阵,并使两者之差尽可能的小。下面主要讨论低阶近似和F-范数。
给定一个M x N矩阵C(其秩为r)和正整数k,我们希望找到一个M x N矩阵Ck,其秩不大于K。设X为C与Ck之间的差,X=C – Ck,X的F-范数为
当k远小于r时,称Ck为C的低阶近似,其中X也就是两矩阵之差的F范数要尽可能的小。
SVD可以被用与求低阶近似问题,步骤如下:
2. 构造![]() ,它是将
,它是将![]() 的第k+1行至M行设为零,也就是把
的第k+1行至M行设为零,也就是把![]() 的最小的r-k个(the r-k smallest)奇异值设为零。
的最小的r-k个(the r-k smallest)奇异值设为零。
特征值数值的大小对矩阵-向量相乘影响的大小成正比,而奇异值和特征值也是正比关系,因此这里选取数值最小的r-k个特征值设为零合乎情理,即我们所希望的C-Ck尽可能的 小。完整的证明可以在Introduction to Information Retrieval[2]中找到。
我们现在也清楚了LSA的基本思路:LSA希望通过降低传统向量空间的维度来去除空间中的“噪音”,而降维可以通过SVD实现,因此首先对Term-Document矩阵进行SVD分解, 然后降维并构造语义空间。
pca
假设我们矩阵每一行表示一个样本,每一列表示一个feature,用矩阵的语言来表示,将一个m * n的矩阵A的进行坐标轴的变化,P就是一个变换的矩阵从一个N维的空间变换到 另一个N维的空间,在空间中就会进行一些类似于旋转、拉伸的变化。
而将一个m * n的矩阵A变换成一个m * r的矩阵,这样就会使得本来有n个feature的,变成了有r个feature了(r < n),这r个其实就是对n个feature的一种提炼,我们就把这 个称为feature的压缩。用数学语言表示就是:
但是这个怎么和SVD扯上关系呢?之前谈到,SVD得出的奇异向量也是从奇异值由大到小排列的,按PCA的观点来看,就是方差最大的坐标轴就是第一个奇异向量,方差次大的坐标轴就是第二个奇异向量…我们回忆一下之前得到的SVD式子:
(批注:原文公式错误,应为A(mxn)≈U(mxr)*∑(rxr)*V^T(nxr),V是一个nxr的矩阵下同)
在矩阵的两边同时乘上一个矩阵V,由于V是一个正交的矩阵,所以V转置乘以V得到单位阵I,所以可以化成后面的式子
将后面的式子与A * P那个m * n的矩阵变换为m * r的矩阵的式子对照看看,在这里,其实V就是P,也就是一个变化的向量。这里是将一个m * n 的矩阵压缩到一个m * r的矩 阵,也就是对列进行压缩,如果我们想对行进行压缩(在PCA的观点下,对行进行压缩可以理解为,将一些相似的sample合并在一起,或者将一些没有太大价值的sample去 掉) 怎么办呢?同样我们写出一个通用的行压缩例子:
这样就从一个m行的矩阵压缩到一个r行的矩阵了,对SVD来说也是一样的,我们对SVD分解的式子两边乘以U的转置U'
这样我们就得到了对行进行压缩的式子。可以看出,其实PCA几乎可以说是对SVD的一个包装,如果我们实现了SVD,那也就实现了PCA了,而且更好的地方是,有了SVD,我们就可以得到两个方向的PCA,如果我们对A’A进行特征值的分解,只能得到一个方向的PCA
f 范数


Sigmoid函数是一个S型函数. Sigmoid函数的数学公式为

它是常微分方程

的一个解.
Sigmoid函数具有如下基本性质:
- 定义域为
- 值域为
, 为有界函数
- 函数
在定义域内为连续和光滑函数
- 函数
的导数为
- 不定积分为
,
为常数
tanh x=sinh x / cosh x
其中sinh x=(e^(x)-e^(-x))/2 ,cosh x=(e^x+e^(-x))/2
所以tanhx = (e^(x)-e^(-x)) /(e^x+e^(-x))
传统IR领域内文本相似度比较所采用的经典方法是文本相似度的向量夹角余弦,其主要思想是根据一个文章中出现词的词频构成一个向量,然后计算两篇文章对应向量的向量夹角。但由于有可能一个文章的特征向量词特别多导致整个向量维度很高,使得计算的代价太大,对于Google这种处理万亿级别的网页的搜索引擎而言是不可接受的,simhash算法的主要思想是降维,将高维的特征向量映射成一个f-bit的指纹(fingerprint),通过比较两篇文章的f-bit指纹的Hamming Distance来确定文章是否重复或者高度近似。
simhash算法很精巧,但却十分容易理解和实现,具体的simhash过程如下:
1. 首先基于传统的IR方法,将文章转换为一组加权的特征值构成的向量。
2.初始化一个f维的向量V,其中每一个元素初始值为0。
3.对于文章的特征向量集中的每一个特征,做如下计算:
利用传统的hash算法映射到一个f-bit的签名。对于这个f- bit的签名,如果签名的第i位上为1,则对向量V中第i维加上这个特征的权值,否则对向量的第i维减去该特征的权值。
4.对整个特征向量集合迭代上述运算后,根据V中每一维向量的符号来确定生成的f-bit指纹的值,如果V的第i维为正数,则生成f-bit指纹的第i维为1,否则为0。
simhash和普通hash最大的不同在于传统的hash函数虽然也可以用于映射来比较文本的重复,但是对于可能差距只有一个字节的文档也会映射成两个完全不同的哈希结果,而simhash对相似的文本的哈希映射结果也相似。Google的论文中取了f=64,即将整个网页的加权特征集合映射到一个64-bit的fingerprint上。
比起simhash,整片文章中Google所采用的查找与给定f-bit的fingerprint的海明距离(Hamming Distance)小于k的算法相对还稍微难理解点。
fingerprint的Hamming Distance
问题:一个80亿的64-bit指纹组成的集合Q,对于一个给定64-bit的指纹F,如何在a few millionseconds中找到Q中和f至多只有k(k=3)位差别的指纹。
思想:1. 对于一个具有2^d个记录的集合,只需要考虑d-bit hash。2. 选取一个d’使得|d’-d|十分小,因此如果两fingerprint在d’-bits上都相同,那么在d-bits也很可能相同。然后在这些d-bit match的结果中寻找整个f-bit的Hamming Distance小于k的fingerprint。简单的说,就是利用fingerprint少量特征位数比较从而首先缩小范围,然后再去确定是否差异小于k个bit。
算法:
1. 首先对于集合Q构建多个表T1,T2…Tt,每一个表都是采用对应的置换函数π(i)将64-bit的fingerprint中的某p(i)位序列置换换到整个序列的最前面。即每个表存储都是整个Q的fingerprint的复制置换。
2.对于给定的F,在每个Ti中进行匹配,寻找所有前pi位与F经过π(i)置换后的前pi位相同的fingerprint。
3.对于所有在上一步中匹配到的置换后的fingerprint,计算其是否与π(i)(F)至多有k-bit不同。
算法的重点在于对于集合Q的分表以及每个表所对应的置换函数,假设对于64-bit的fingerprint,k=3,存储16个table,划分参考下图:
将64-bit按照16位划分为4个区间,每个区间剩余的48-bit再按照每个12-bit划分为4个区间,因此总共16个table并行查找,即使三个不同的k-bit落在A、B、C、D中三个不同的区块,此划分方法也不会导致遗漏。
以上方法是对于online的query,即一个给定的F在集合中查找相似的fingerprint。如果爬虫每天爬取了100w个网页,快速的查找这些新抓取的网页是否在原集合中有Near-duplication,对于这种batch-query的情况,Map-Reduce就发挥它的威力了。
不同的是,在batch-query的处理中,是对待查集合B(1M个fingerprint)进行复制置换构建Table而非8B的目标集合,而在每一个chunkserver上对Fi(F为整个8B的fingerprint)在整个Table(B)中进行探测,每一个chunkserver上的的该Map过程输出该Fi中与整个B的near-duplicates,Reduces过程则将所有的结果收集、去重、然后输出为一个sorted file。
Haffman编码压缩
上述的查询过程,特别是针对online-version的算法,可以看出需要对8B的fingerprint进行多表复制和构建,其占据的容量是非常大的,不过由于构建的每一个置换Table都是sorted的,因此可以利用每一个fingerprint与其前一个的开始不同的bit-position h(h∈[0,f-1]) 来进行数据压缩,即如果前一个编码是11011011,而自身是11011001,则后一个可以编码为(6)1,即h=6,其中6表示从第6位(从0开始编号)开始和上一个fingerprint不相同(上一个为1,这个必然为0),然后再保存不相同位置右侧的编码,依次生成整个table。
Google首先计算整个排序的fingerprint表中h的分布情况,即不同的h出现次数,依据此对[0,f-1]上出现的h建立Haffman code,再根据上述规则生成table(例如上面的6就表示成对应的Haffman code)。其中table分为多个block,每一个block中的第一个fingerprint保存原数据,后面的依次按照编码生成。
将每一个block中所对应的最后一个fingerprint保存在内存中,因此在比对的时候就可以直接根据内存中的fingerprint来确定是哪一个block需要被decompress进行比较。
8B个64-bit的fingerprint原占据空间大约为64GB,利用上述Haffman code压缩后几乎会减少一般,而内存中又只对每一个block保存了一个fingerprint。
每次看Google的论文都会让人眼前一亮,而且与很多(特别是国内)的论文是对未来进行设想不同,Google的东西都是已经运行了2,3年了再到WWW,OSDI这种顶级会议上灌个水。再次各种羡慕能去这个Dream Company工作的人.
20. bloomfilter
Bloom Filter是一种空间效率很高的随机数据结构,它的原理是,当一个元素被加入集合时,通过K个Hash函数将这个元素映射成一个位阵列(Bit array)中的K个点,把它们置为1。检索时,我们只要看看这些点是不是都是1就(大约)知道集合中有没有它了:如果这些点有任何一个0,则被检索元素一定不在;如果都是1,则被检索元素很可能在。这就是布隆过滤器的基本思想。
但Bloom Filter的这种高效是有一定代价的:在判断一个元素是否属于某个集合时,有可能会把不属于这个集合的元素误认为属于这个集合(false positive)。因此,Bloom Filter不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下,Bloom Filter通过极少的错误换取了存储空间的极大节省。
下面我们具体来看Bloom Filter是如何用位数组表示集合的。初始状态时,Bloom Filter是一个包含m位的位数组,每一位都置为0。

为了表达S={x1, x2,…,xn}这样一个n个元素的集合,Bloom Filter使用k个相互独立的哈希函数(Hash Function),它们分别将集合中的每个元素映射到{1,…,m}的范围中。对任意一个元素x,第i个哈希函数映射的位置hi(x)就会被置为1(1≤i≤k)。注意,如果一个位置多次被置为1,那么只有第一次会起作用,后面几次将没有任何效果。在下图中,k=3,且有两个哈希函数选中同一个位置(从左边数第五位,即第二个“1“处)。

在判断y是否属于这个集合时,我们对y应用k次哈希函数,如果所有hi(y)的位置都是1(1≤i≤k),那么我们就认为y是集合中的元素,否则就认为y不是集合中的元素。下图中y1就不是集合中的元素(因为y1有一处指向了“0”位)。y2或者属于这个集合,或者刚好是一个false positive。

前面我们已经提到了,Bloom Filter在判断一个元素是否属于它表示的集合时会有一定的错误率(false positive rate),下面我们就来估计错误率的大小。在估计之前为了简化模型,我们假设kn<m且各个哈希函数是完全随机的。当集合S={x1, x2,…,xn}的所有元素都被k个哈希函数映射到m位的位数组中时,这个位数组中某一位还是0的概率是:

其中1/m表示任意一个哈希函数选中这一位的概率(前提是哈希函数是完全随机的),(1-1/m)表示哈希一次没有选中这一位的概率。要把S完全映射到位数组中,需要做kn次哈希。某一位还是0意味着kn次哈希都没有选中它,因此这个概率就是(1-1/m)的kn次方。令p = e-kn/m是为了简化运算,这里用到了计算e时常用的近似:
令ρ为位数组中0的比例,则ρ的数学期望E(ρ)= p’。在ρ已知的情况下,要求的错误率(false positive rate)为:

(1-ρ)为位数组中1的比例,(1-ρ)k就表示k次哈希都刚好选中1的区域,即false positive rate。上式中第二步近似在前面已经提到了,现在来看第一步近似。p’只是ρ的数学期望,在实际中ρ的值有可能偏离它的数学期望值。M. Mitzenmacher已经证明[2] ,位数组中0的比例非常集中地分布在它的数学期望值的附近。因此,第一步的近似得以成立。分别将p和p’代入上式中,得:


相比p’和f’,使用p和f通常在分析中更为方便。
既然Bloom Filter要靠多个哈希函数将集合映射到位数组中,那么应该选择几个哈希函数才能使元素查询时的错误率降到最低呢?这里有两个互斥的理由:如果哈希函数的个数多,那么在对一个不属于集合的元素进行查询时得到0的概率就大;但另一方面,如果哈希函数的个数少,那么位数组中的0就多。为了得到最优的哈希函数个数,我们需要根据上一小节中的错误率公式进行计算。
先用p和f进行计算。注意到f = exp(k ln(1 − e−kn/m)),我们令g = k ln(1 − e−kn/m),只要让g取到最小,f自然也取到最小。由于p = e-kn/m,我们可以将g写成

根据对称性法则可以很容易看出当p = 1/2,也就是k = ln2· (m/n)时,g取得最小值。在这种情况下,最小错误率f等于(1/2)k≈ (0.6185)m/n。另外,注意到p是位数组中某一位仍是0的概率,所以p = 1/2对应着位数组中0和1各一半。换句话说,要想保持错误率低,最好让位数组有一半还空着。
需要强调的一点是,p = 1/2时错误率最小这个结果并不依赖于近似值p和f。同样对于f’ = exp(k ln(1 − (1 − 1/m)kn)),g’ = k ln(1 − (1 − 1/m)kn),p’ = (1 − 1/m)kn,我们可以将g’写成

同样根据对称性法则可以得到当p’ = 1/2时,g’取得最小值。
下面我们来看看,在不超过一定错误率的情况下,Bloom Filter至少需要多少位才能表示全集中任意n个元素的集合。假设全集中共有u个元素,允许的最大错误率为є,下面我们来求位数组的位数m。
假设X为全集中任取n个元素的集合,F(X)是表示X的位数组。那么对于集合X中任意一个元素x,在s = F(X)中查询x都能得到肯定的结果,即s能够接受x。显然,由于Bloom Filter引入了错误,s能够接受的不仅仅是X中的元素,它还能够є (u - n)个false positive。因此,对于一个确定的位数组来说,它能够接受总共n + є (u - n)个元素。在n + є (u - n)个元素中,s真正表示的只有其中n个,所以一个确定的位数组可以表示

个集合。m位的位数组共有2m个不同的组合,进而可以推出,m位的位数组可以表示

个集合。全集中n个元素的集合总共有

个,因此要让m位的位数组能够表示所有n个元素的集合,必须有

即:

上式中的近似前提是n和єu相比很小,这也是实际情况中常常发生的。根据上式,我们得出结论:在错误率不大于є的情况下,m至少要等于n log2(1/є)才能表示任意n个元素的集合。
上一小节中我们曾算出当k = ln2· (m/n)时错误率f最小,这时f = (1/2)k= (1/2)mln2 / n。现在令f≤є,可以推出

这个结果比前面我们算得的下界n log2(1/є)大了log2e≈ 1.44倍。这说明在哈希函数的个数取到最优时,要让错误率不超过є,m至少需要取到最小值的1.44倍。
在计算机科学中,我们常常会碰到时间换空间或者空间换时间的情况,即为了达到某一个方面的最优而牺牲另一个方面。Bloom Filter在时间空间这两个因素之外又引入了另一个因素:错误率。在使用Bloom Filter判断一个元素是否属于某个集合时,会有一定的错误率。也就是说,有可能把不属于这个集合的元素误认为属于这个集合(False Positive),但不会把属于这个集合的元素误认为不属于这个集合(False Negative)。在增加了错误率这个因素之后,Bloom Filter通过允许少量的错误来节省大量的存储空间。
自从Burton Bloom在70年代提出Bloom Filter之后,Bloom Filter就被广泛用于拼写检查和数据库系统中。近一二十年,伴随着网络的普及和发展,Bloom Filter在网络领域获得了新生,各种Bloom Filter变种和新的应用不断出现。可以预见,随着网络应用的不断深入,新的变种和应用将会继续出现,Bloom Filter必将获得更大的发展。
可以用来实现数据字典,进行数据的判重,或者集合求交集


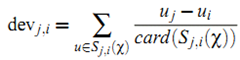
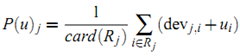
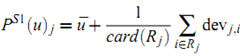


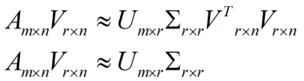
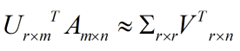





 浙公网安备 33010602011771号
浙公网安备 33010602011771号