深度优先搜索
深度优先搜索
概述
- 定义
深度优先搜索是对一个连通图进行遍历的算法
算法是作用于具体数据结构之上的,深度优先搜索算法是基于“图”这种数据结构的
- 适用场景
深度优先搜索适合节点数量多,树的层次比较深的情况下
DFS适合的题目:给定初始状态跟目标状态,要求判断从初始状态到目标状态是否有解
- 优缺点
深度优先搜索 缺点:难以寻找最优解 优点:内存消耗小
- 搜索算法
图上的搜索算法,就是在图中找一个顶点出发,到另一个顶点的位置
深度优先搜索算法属于回溯思想,这种思想解决问题的过程适合用递归实现
深度优先搜索的搜索过程及代码实现
我们一起看下图,搜索的起始顶点是s,终止顶点是t,要在图中寻找一条s到t的路径。图中实线表示遍历,虚线表示回退,整个深度递归算法的搜索路劲如箭头方向所示。
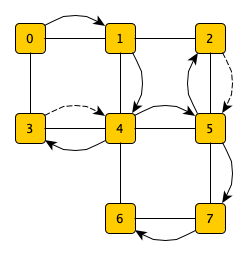
我们来实现下该图的路径寻找,并打印出该路径
-
使用Java实现
-
Graph.java
图的存储,将上图存储到图结构中
我们这里使用邻接表的方式存储
import java.util.LinkedList;
//存储结构无向图
public class Graph {
private int vertex; //顶点个数
public LinkedList<Integer> Adjacency[];//邻接表
/**
* 邻接表方式存储
* @param vertex int 顶点个数
*/
public Graph(int vertex) {
this.vertex = vertex;
Adjacency = new LinkedList[vertex];
for (int i=0; i<vertex; ++i) {
Adjacency[i] = new LinkedList<>();
}
}
/**
* 无向图的一条边存两次
* @param s int 起始顶点
* @param t int 终止顶点
*/
public void addEdge(int s, int t) {
Adjacency[s].add(t);
Adjacency[t].add(s);
}
}
- DepthFirstSearch.java
import java.lang.System;
public class DepthFirstSearch {
private static int vertex; //顶点个数
private static Graph g;//图的存储
static boolean found = false;
public static void main(String[] args){
vertex = 8;
g = new Graph(vertex);
g.addEdge(0,1);
g.addEdge(0,3);
g.addEdge(1,4);
g.addEdge(1,2);
g.addEdge(2,5);
g.addEdge(3,4);
g.addEdge(4,5);
g.addEdge(4,6);
g.addEdge(5,7);
g.addEdge(6,7);
DFSraverse(0, 6);
}
public static void DFSraverse(int s, int t) {
found = false;
boolean[] visited = new boolean[vertex];//记录访问状态
int[] prev = new int[vertex];//记录搜索路径
for (int i=0; i<vertex; ++i) {
prev[i] = -1;
}
dfs(s, t, visited, prev);
print(prev, s, t);
}
public static void dfs(int w, int t, boolean[] visited, int[] prev) {
if(found==true) return;
visited[w] = true;//记录节点已经被访问
if(w==t) {//起始顶点等于终止顶点
found = true;
return;
}
//对每个顶点的链表进行遍历(邻接表存储方式,每个顶点存储指向顶点的链表,无向链表一个边要存储两次)
for (int i=0; i<g.Adjacency[w].size(); ++i) {
int q = g.Adjacency[w].get(i);
if(!visited[q]) {
prev[q] = w;
dfs(q, t, visited, prev);
}
}
}
private static void print(int[] prev, int s, int t) { // 递归打印s->t的路径
if (prev[t] != -1 && t != s) {
print(prev, s, prev[t]);
}
System.out.print(t + " ");
}
}
- 运行
javac DepthFirstSearch.java
java DepthFirstSearch
0 1 4 5 7 6
- 搜索过程简述
存储好图结构,调用函数DFSraverse进入搜索
初始化布尔数据visited用于记录某个顶点是否有被访问过,在深度优先搜索中,被访问过的节点不会再次被访问
初始化整型数据prev用于记录搜索路径,也用于搜索路径结果输出,给prev数组中每个订单赋值为-1,表示该顶点没有被访问过,用于输出控制
调用dfs进入搜索,深度优先搜索的本质是递归
found表示已经到达终点顶点,如果已经到终点则直接返回
visited记录当前顶点已经被访问
接着遍历顶点的子链表(即顶点的连接点)
如果有未访问过的连接点(被访问过表示该顶点走不通,无法到达终点顶点),则直接递归调用该连接点的连接点(往深度搜索)
重复该递归调用,直到找到终点顶点,设置found为true,函数返回
深度优先搜索的时间、空间复杂度
- 时间复杂度
从前面的图可以看出来,每条边最多被访问两次,一次是遍历,一次回退,所以深度优先搜索算法的时间复杂度是O(E),E表示边的个数。
- 空间复杂度
深度优先搜索算法的消耗内存主要是visited,prev数组和递归调用栈。visited、prev数组的大小跟顶点的个数V成正比,递归调用栈的最大深度不会超过顶点的个数,所以总的空间复杂度就是O(V)。
实践
接下来一起看看leetcode上的一道题来加深理解
该题求解电话号码的组合,可以使用深度优先搜索求解
- 使用GO实现
func letterCombinations(digits string) []string {
var data []string
digits_arr := strings.Split(digits, "")
start := 97//a的ASCII十进制值
var ca_len int//每个数字对应的字母长度为3,z特殊对应四位
var match_letter string
setp := make(map[string]int)
//拿到所有的字母
for _,val := range digits_arr {
var_int,err := strconv.Atoi(val)
if(err!=nil) {
return data
}
//7、9对应4个字母
ca_len = 3
if(var_int==9 || var_int==7) {
ca_len = ca_len+1
}
start_distrbute_num := (var_int - 2)*3
if(var_int==8 || var_int==9) {
start_distrbute_num = start_distrbute_num+1
}
rel_start := start + start_distrbute_num
for i := 0; i < ca_len; i++ {
match_letter_num := rel_start + i
letter := string(rune(match_letter_num))
setp[letter] = ca_len
match_letter += letter
}
}
letters_arr := strings.Split(match_letter, "")
data = dfsLetter(letters_arr, setp)
return data
}
func dfsLetter(letters_arr []string, setp map[string]int) []string {
var _step int
var data []string
t := 0
for __key,letter := range letters_arr {
_step = setp[letter]
//顶点只循环第一轮[即第一个数字]
//超过一个数字的放到递归中
if(__key==0) {
t = len(letters_arr[:_step])
//count_step = _step
}
if(t!=0 && __key>=t) {
continue
}
//存在下一个数
if(len(letters_arr[_step:])>0) {
//去除步长之后的字母继续循环
_match_letter_arr := letters_arr[_step:]
res := dfsLetter(_match_letter_arr, setp)
for _, _key := range res {
r := letter + _key
data = append(data, r)
}
} else {
//没有产生递归返回数据,即当前只有一个数字
data = append(data, letter)
}
}
return data
}
func main() {
digits := "6789"
data := letterCombinations(digits)
fmt.Println("v%", data)
}
- 运行
go run letterCombinations.go
[mptw mptx mpty mptz mpuw mpux mpuy mpuz mpvw mpvx mpvy mpvz mqtw mqtx mqty mqtz mquw mqux mquy mquz mqvw mqvx mqvy mqvz mrtw mrtx mrty mrtz mruw mrux mruy mruz mrvw mrvx mrvy mrvz mstw mstx msty mstz msuw msux msuy msuz msvw msvx msvy msvz nptw nptx npty nptz npuw npux npuy npuz npvw npvx npvy npvz nqtw nqtx nqty nqtz nquw nqux nquy nquz nqvw nqvx nqvy nqvz nrtw nrtx nrty nrtz nruw nrux nruy nruz nrvw nrvx nrvy nrvz nstw nstx nsty nstz nsuw nsux nsuy nsuz nsvw nsvx nsvy nsvz optw optx opty optz opuw opux opuy opuz opvw opvx opvy opvz oqtw oqtx oqty oqtz oquw oqux oquy oquz oqvw oqvx oqvy oqvz ortw ortx orty ortz oruw orux oruy oruz orvw orvx orvy orvz ostw ostx osty ostz osuw osux osuy osuz osvw osvx osvy osvz]
- 分析
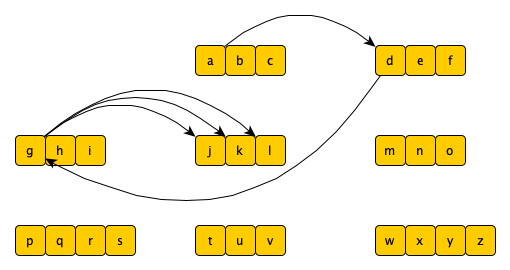
同样我们通过画图来分析
假设我们填写的数字是"2345"[题目限制要求最多填写四个数字]
首先我们把输入的数字转换成对应的字母,我采用的是ASCII码的方式
转换后调用函数dfsLetter进行字符拼接,进入函数后即遍历字母切片,仅遍历第一个数字对应的字母
如果存在下一个数字(前序记录好数字对应字母长度),即遍历调用dfsLetter,接受遍历的字母组合返回
如果是最后一个数字,则返回当前字母组合
以“2345”为例,从数字2开始,循环遍历拿到a,存在数字3,则找到字母d,存在数字4,找到字母g,存在数字5,找到字母j,没有下一个数字,则继续拿到j、k、l,然后与g组装返回,gj、gk、gl,接着返回给d,组成dgj、dgk、dgl,然后再返回上层调用,组成adgj、adgk、adgl,然后继续循环字母b,重复之前的调用步骤,直到找到所有的字母组合。
其他要注意的地方:
数字7跟数字9的字母长度是4位,要特别注意
- 参考


 浙公网安备 33010602011771号
浙公网安备 33010602011771号