SMU Summer 2024 Contest Round 4
A Made Up
思路:统计A的个数,O(1)统计cnt[bc]
void solve() {
int n;
cin >> n;
vector<int> cnt (n + 1), b(n + 1);
for (int i = 1; i <= n; ++i) {
int x;
cin >> x;
cnt[x] ++;
}
for (int i = 1; i <= n; ++i) {
cin >> b[i];
}
int ans = 0;
for (int i = 1; i <= n; ++i) {
int x;
cin >> x;
ans += cnt[b[x]];
}
cout << ans;
}B H and V
思路:用二进制暴力枚举所选行、所选列的,然后枚举统计剩余black的个数
void solve() {
int n, m, k;
cin >> n >> m >> k;
vector<string> ve (n);
for (int i = 0; i < n; ++i) {
cin >> ve[i];
}
int ans = 0;
for (int i = 0; i < pow(2, n); ++i) {
for (int j = 0; j < pow(2, m); ++j) {
int cnti = 0, cntj = 0;
vector<vector<int> > st(n, vector<int> (m));
for (int ii = 0; ii < n; ++ii) {
if ((i >> ii) & 1) {
for (int jj = 0; jj < m; ++jj) {
st[ii][jj] = 1;
}
}
}
for (int ii = 0; ii < m; ++ii) {
if ((j >> ii) & 1) {
for (int jj = 0; jj < n; ++jj) {
st[jj][ii] = 1;
}
}
}
for (int ii = 0; ii < n; ++ii) {
for (int jj = 0; jj < m; ++jj) {
if (!st[ii][jj]) {
// cout << ve[ii][jj];
if (ve[ii][jj] == '#') cnti ++;
else if (ve[ii][jj] == '.') cntj ++;
}
// else cout << '_';
}
// cout << '\n';
}
if (cnti == k) {
ans ++;
// cout << "Y\n";
}
}
}
cout << ans;
}C Moving Piece
思路:不管从哪个i出发,之后的路径是已定的,并且如果一直进行下去,会形成循环节,且循环长度最大为n。
那么就可以枚举从所有点出发求出可以获得的最大值,先求出循环节,若一次循环下来的贡献是正数,则可以一直进行下去,若是负数,那就在循环里找出最大值即可。
对于一次循环的贡献是正数的情况, 应该进行更多次循环,但是循环中存在负数,且不确定负数在循环中的位置,直接暴力枚举最后两次完整循环的过程中的最大答案
void solve() {
int n, k;
cin >> n >> k;
vector<int> p(n + 1), c(n + 1);
for (int i = 1; i <= n; ++i) cin >> p[i];
for (int i = 1; i <= n; ++i) cin >> c[i];
int ans = LLONG_MIN;
for (int i = 1; i <= n; ++i) {
vector<int> st(n + 1), sum;
int idx = i, now = 0;
while (!st[idx]) {
st[idx] = 1;
now += c[idx];
sum.push_back(now);
idx = p[idx];
}
int res = LLONG_MIN;
// cout << "size:";
// cout << sum.size() << '\n';
// for (auto v:sum) cout << v << ' ';
// cout << '\n';
if (sum.back() <= 0) {
for (int j = 0; j < sum.size() && j < k; ++j) {
res = max(res, sum[j]);
}
} else {
int all = 0;
int cnt = max((k / (int)(sum.size())) - 2, 0ll);
all += cnt * sum.back();
if (cnt > 0) res = max(res, all);
if (k >= sum.size()) {
for (int j = 0; j < sum.size(); ++j) {
res = max(res, all + sum[j]);
}
all += sum.back();
}
if (k >= 2 * sum.size()) {
for (int j = 0; j < sum.size(); ++j) {
res = max(res, all + sum[j]);
}
all += sum.back();
}
for (int j = 0; j < k % ((int)sum.size()); ++j) {
res = max(res, all + sum[j]);
}
}
// cout << i << ' ' << res << '\n';
ans = max(ans, res);
}
cout << ans;
}D Sum of Divisors
思路:类似质数筛的方法,枚举因子,这样是nlogn的
void solve() {
int n;
cin >> n;
vector<int> f(n + 1, 0);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j * i <= n; ++j) {
f[i * j] ++;
}
}
int ans = 0;
for (int i = 1; i <= n; ++i) {
ans += i * f[i];
}
cout << ans;
}E Red and Green Apples
思路:c可以转换为a或b,那就将abc全部合在一起排序,优先取最大的,保证abc选的个数和不超过x + y
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define PII pair<int, int>
const int N = 2e5 + 5, mod = 998244353;
struct E {
int x, id;
bool operator <(const E &e)const {
return x < e.x;
}
};
void solve() {
int x, y, a, b, c;
cin >> x >> y >> a >> b >> c;
priority_queue<E> q;
for (int i = 0; i < a; ++i) {
int x;
cin >> x;
q.push({x, 1});
}
for (int i = 0; i < b; ++i) {
int x;
cin >> x;
q.push({x, 2});
}
for (int i = 0; i < c; ++i) {
int x;
cin >> x;
q.push({x, 3});
}
int ans = 0, z = 0;
while ((x > 0 || y > 0) && q.size() && z < x + y) {
auto [w, id]=q.top();
// cout << w << '\n';
q.pop();
if (id == 1 && x > 0) {
ans += w, x --;
}
if (id == 2 && y > 0) {
ans += w, y --;
}
if (id == 3) {
ans += w, z ++;
}
}
cout << ans;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int T = 1;
// cin >> T;
while (T--) {
solve();
}
return 0;
}F Rem of Sum is Num
思路:令n = ak + b,在满足题目的条件下,n = sum[r] - sum[l - 1],b = r - l + 1,代入得到 sum[r] - sum[l - 1] = ak + r - l + 1,转换一下得到 ak = (sum[r] - r) - (sum[l - 1] - (l - 1)),且由于r - l + 1为k的余数,所以b < k,且统计sum[i] - i对k取模后的数的个数,注意只统计r - l + 1 <= k的
void solve() {
int n, k;
cin >> n >> k;
vector<int> a (n + 1), sum(n + 1);
for (int i = 1; i <= n; ++i) {
cin >> a[i];
sum[i] = sum[i - 1] + a[i];
}
for (int i = 1; i <= n; ++i) {
sum[i] -= i;
}
map<int, int> mp;
mp[0] ++;
int ans = 0;
int l = 0;
for (int i = 1; i <= n; ++i) {
if (l < i - k + 1) {
mp[sum[l++] % k] --;
}
int c = sum[i] % k;
// cout << sum[i] << ' ' << c << '\n';
ans += mp[c];
mp[c] ++;
}
cout << ans;
}G Keep Connect
思路:线性dp,f[i][j][k]表示前i列,已经删除j条边,当前上下边连通情况k(连通/不连通)
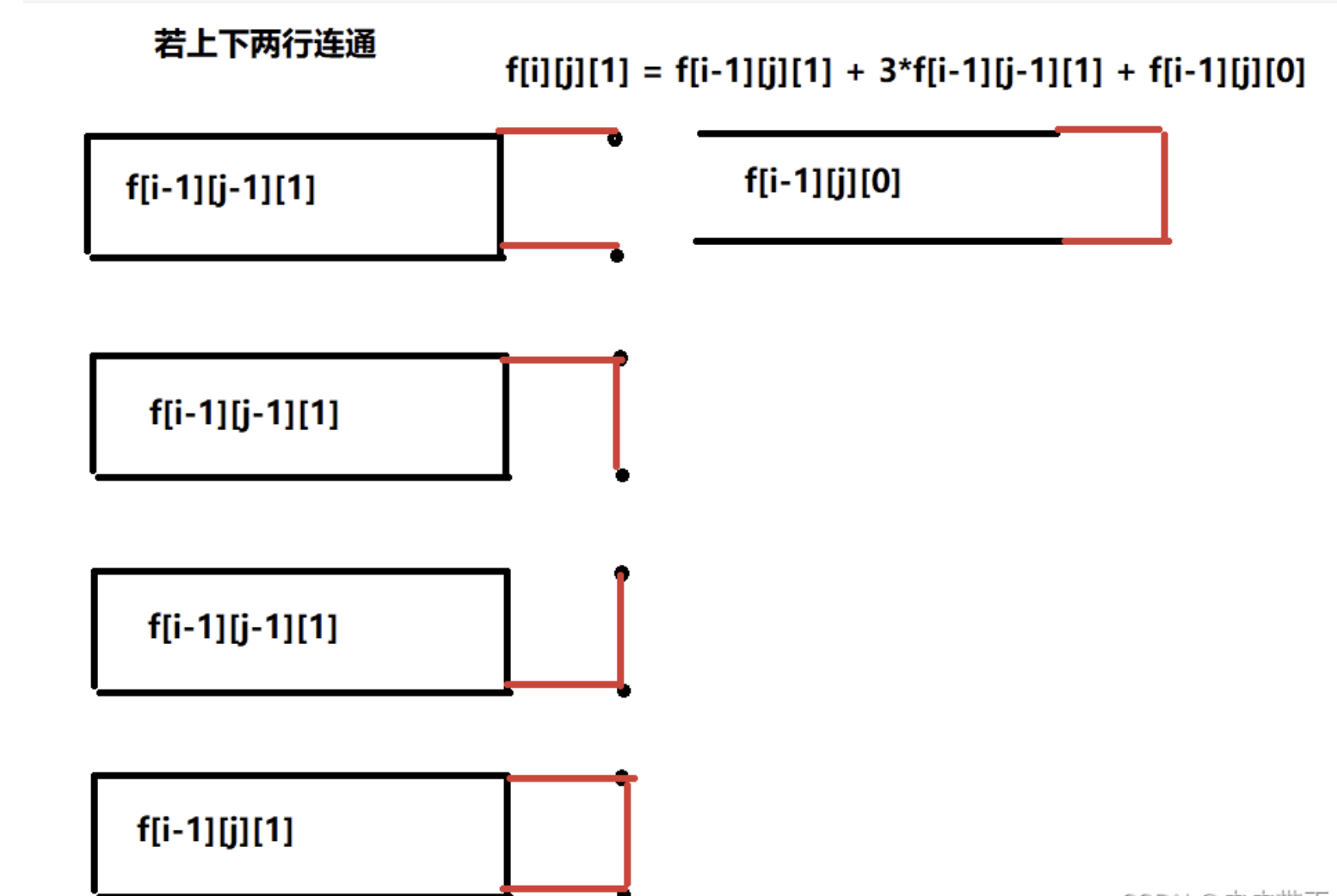
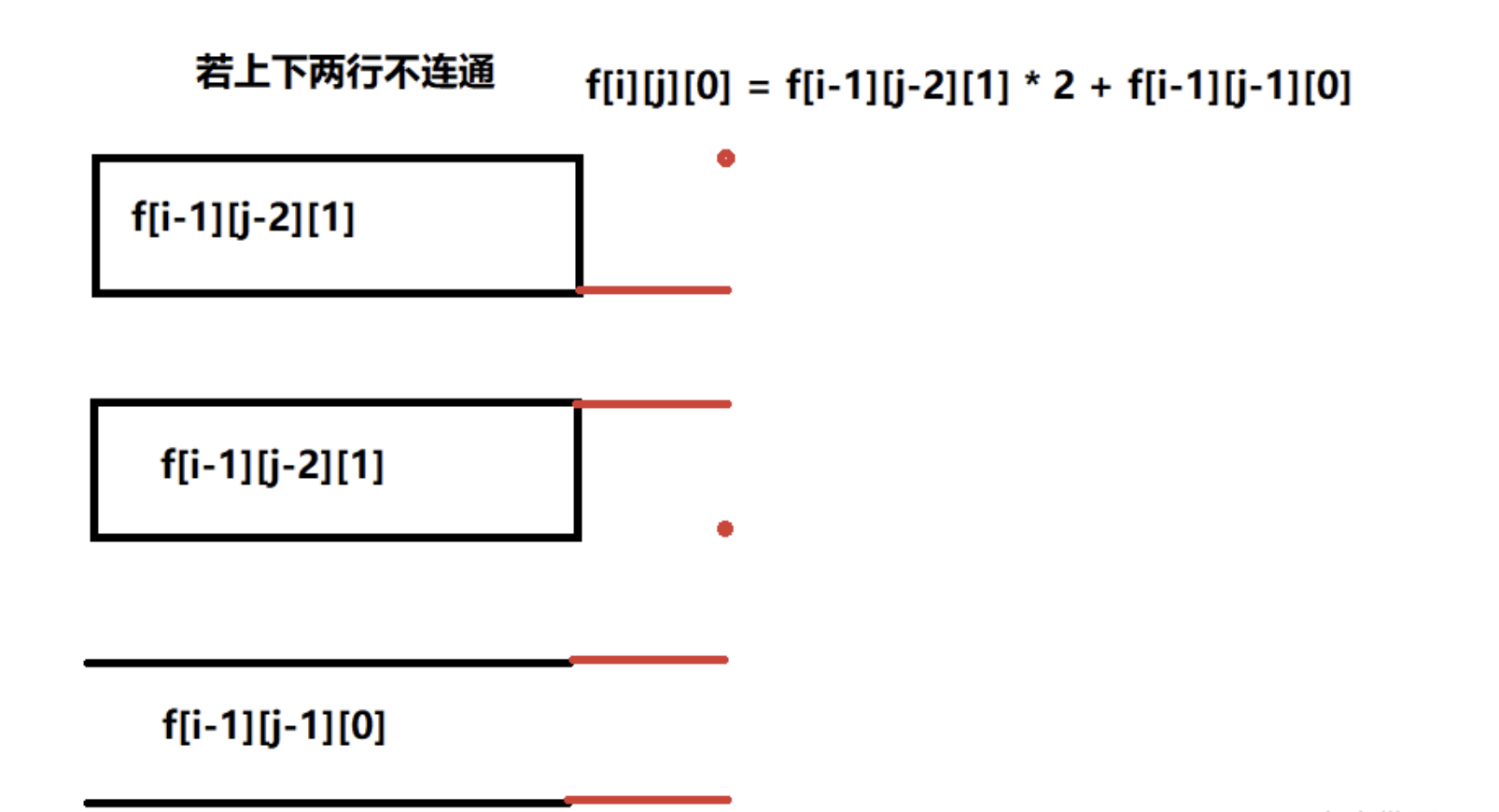
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define PII pair<int, int>
const int N = 3e3 + 5, mod = 998244353;
int f[N][N][2];
void solve() {
int n, p;
cin >> n >> p;
// vector<vector<vector<int> > > f(n + 1, vector<vector<int> > (n - 1, vector<int> (2)));
f[1][1][0] = f[1][0][1] = 1;
for (int i = 1; i <= n; ++i) f[i][0][1] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j <= i; ++j) {
f[i][j][1] = (f[i - 1][j][1] + 3 * f[i - 1][j - 1][1] % p + f[i - 1][j][0]) % p;
if (j >= 2) f[i][j][0] = (f[i][j][0] + 2 * f[i - 1][j - 2][1] % p) % p;
f[i][j][0] = (f[i][j][0] + f[i - 1][j - 1][0]) % p;
}
}
for (int i = 1; i < n; ++i) cout << f[n][i][1] << ' ';
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int T = 1;
// cin >> T;
while (T--) {
solve();
}
return 0;
}



