SMU Summer 2024 Contest Round 1（7.8）

A_Dice and Coin

题目链接：abc126_c

思路：分别求所有掷到的筛子数时赢得可能，进行求和

void solve() {
    int n, k;
    cin >> n >> k;
    double ans = 0;

    for (int i = 1; i <= n; ++i) {
        double now = 1.0 / n;
        if (i >= k) ans += now;
        else {
            int j = i;
            while (j < k) {
                now *= 0.5, j *= 2;
            }
            ans += now;
        }

    }
    cout << fixed << setprecision(12) << ans;
}

B_equeue

题目链接：abc128_d

思路：操作的先后顺序不定，所以可以考虑将数取出，再将最小的数放回去。

用[i][j]维护前i个数中保留j个数在手中的最大值，求出前后缀的[i][j]后，枚举前i个数保留cnti个，后j个保留cntj个的答案最大值

 

void solve() {
    int n, k;
    cin >> n >> k;
    vector<int> ve(n + 1);
    for (int i = 1; i <= n; ++i) cin >> ve[i];

    vector<vector<int> > l(n + 5, vector<int> (n + 5, 0));
    vector<vector<int> > r(n + 5, vector<int> (n + 5, 0));

    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= i; ++j) {
            l[i][j] = l[i - 1][j - 1] + ve[i];
            if (i - 1 >= j) l[i][j] = max(l[i][j], l[i - 1][j]);
        }
    }
    reverse(ve.begin() + 1, ve.end());
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= i; ++j) {
            r[i][j] = r[i - 1][j - 1] + ve[i];
            if (i - 1 >= j) r[i][j] = max(r[i][j], r[i - 1][j]);

        }
    }
    int ans = 0;
    for (int i = 0; i <= n; ++i) {
        for (int cnti = 0; cnti <= i; ++cnti) {
            for (int j = 0; j <= k - i && j <= n - i; ++j) {
                for (int cntj = 0; cntj <= j; ++cntj) {
                    if (i + j + i - cnti + j - cntj > k) continue;
                    ans = max(ans, l[i][cnti] + r[j][cntj]);
                }
            }

        }
    }
    cout << ans;
}

C_Sequence Decomposing

题目链接：abc134_e

思路：用multiset维护所有颜色的末端（即该颜色最大的数），枚举所有数，若没有小于该数的颜色，则插入新的颜色；若有，则选择数最大的颜色为该数颜色

void solve() {
    int n;
    cin >> n;
    vector<int> ve(n);
    for (int i = 0; i < n; ++i) cin >> ve[i];
    multiset<int> se;
    for (int i = 0; i < n; ++i) {
        auto p = se.lower_bound(ve[i]);
        if (p == se.begin()) {
            se.insert(ve[i]);
        } else {
            p --;
            se.erase(p);
            se.insert(ve[i]);
        }
    }
    cout << (int)se.size();
}

 

D_Cell Distance

题目链接：abc127_e

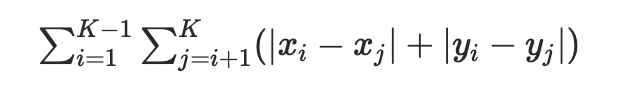
思路：由这个公式可以看出x和y的贡献是独立的，可以分别求。

考虑枚举长度d，对于x来说长度为d的方案由n-d种，将y的方案加进去后的总方案由（n - d）* m * m种，带来的贡献为（n - d）* m * m * d，其余的点任选，所以最后还要乘上C(nm - 2， k - 2)

对于y来说同理。

#include <bits/stdc++.h>

using namespace std;

#define int long long
//#define double long double
const int N = 2e5 + 5, mod = 1e9 + 7;

int ksm(int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) res = res * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return res;
}

int fact[N], infact[N];

int C (int a, int b) {
    if (b == 0) return 1;
    return fact[a] * infact[b] % mod * infact[a - b] % mod;
}

void solve() {
    fact[0] = infact[0] = 1;
    for (int i = 1; i <= 2e5; ++i) {
        fact[i] = fact[i - 1] * i % mod;
    }
    infact[200000] = ksm(fact[200000], mod - 2);
    for (int i = 2e5 - 1; i >= 1; --i) infact[i] = infact[i + 1] * (i + 1) % mod;
    int n, m, k, ans = 0;
    cin >> n >> m >> k;
    for (int i = 1; i < n; ++i) {
        int s = (n - i) * m % mod * m % mod * i % mod;
        ans = (ans + s) % mod;
    }
    for (int i = 1; i < m; ++i) {
        int s = (m - i) * n % mod * n % mod * i % mod;
        ans = (ans + s) % mod;
    }
    ans = ans * C(n * m - 2, k - 2) % mod;
    cout << ans;
}

signed main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int T = 1;
    while (T --) {
        solve();
    }
    return 0;
}

E_Friendships

题目链接：abc131_e

思路：最多的情况是莲花图（一个点连多个点），个数为n *（n - 1）

若将两个叶子相连，则数量减一，可以减n *（n - 1）个，说明可以构造出个数为0~n *（n - 1）的方案

void solve() {
    int n, k;
    cin >> n >> k;
    int ma = (n - 1) * (n - 2) / 2;
    if (k > ma) {
        cout << -1;
        return ;
    }
    ma -= k;
    vector<PII> ans;
    for (int i = 2; i <= n; ++i) ans.push_back({1, i});
    for (int i = 2; i <= n; ++i) {
        for (int j = i + 1; j <= n; ++j) {
            if (ma > 0) ans.push_back({i, j}), ma --;
            else break;
        }
        if (ma <= 0) break;
    }
    cout << ans.size() << '\n';
    for(auto [x, y]: ans) cout << x <<  ' ' << y << '\n';
}

F_Integer Cards

题目链接：abc127_d

思路：最终一定是用最大的数去替换，且最多换n个，那么直接取出最大的n个，去替换原有的数中最小的

void solve() {
    int n, m;
    cin >> n >> m;
    priority_queue<int, vector<int>, greater<int> > q;
    priority_queue<int> tt;
    for (int i = 0; i < n; ++i) {
        int x;
        cin >> x;
        q.push(x);
    }
    vector<PII> ve(m);
    for (int i = 0; i < m; ++i) cin >> ve[i].second >> ve[i].first;
    sort(ve.begin(), ve.end(), cmp);
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < ve[i].second && tt.size() < n; ++j) {
            tt.push(ve[i].first);
        }
        if (tt.size() >= n) break;
    }
//    cout << tt.top() << '\n';
    while (q.size() && tt.size()) {
        int t = q.top(), to = tt.top();
        if (to > t) {
            tt.pop(), q.pop();
            q.push(to);
        } else break;
    }
    int ans = 0;
    while (q.size()) {
        int t = q.top();
        q.pop();
        ans += t;
    }
    cout << ans;
}