欧拉函数及其证明

欧拉函数定义：phi(n) = 1到n中与n互质的数的个数

　　有公式：　phi(n) = n* ∏ ( 1 - 1/pi )  其中p为n的所有质因子,每个质因子只算一次

下面是证明：

1.  当n为质数，显然phi(n) = n-1

2.  当n=p^k  ，其中p为素数

 　　与n不互质的数必定有p因子，把p提出来

　　于是不互质的数有{ p*1, p*2, p*3, ......, p*p^(k-1) }

　　于是互质的数即phi(n)  = p^k - p^(k-1) = p^k  * ( 1 - 1/p )

3.  当n= (x^a)*(y^a), 其中x和y为不相同的素数

　　有phi(n*m)=phi(m)*phi(n) ,  当m和n互质

　　证明这个之前先证明   ( {1, 2, 3, 4, ....n } , {1, 2, 3, 4, ...... m }) 与 {1, 2, 3, 4, ...... m*n } 一一对应  (m,n互质)

　　①从m*n到（m,n）的唯一性

   　　　　m*n中的x，  x%m和x%n有唯一值

　　②从(m,n)到 m*n的唯一性

　　　　设从m中取x，x%m=r

　　　　则x对应m*n中的f可能值为 {r, m+r, 2m+r, 3m+r, .... (n-1)*m+r  }

　　　　这n个数组成了n的完全剩余系

　　　　因为这n个数两两之间的差值可表示为  k* m  (k<n)  

　　　　则 （k*m）%n=0不成立（    k<n , 而gcd(m,n)=1 即 m不提供n的因子 ） 

　　　　即每个数对n取模两两不同，则组成n的完全剩余系

　　　　因此假设再从n中取y， （x，y）可唯一确定一个m*n中的值

　　　　（似乎适用于中国剩余定理）可拓展到多维，即多个互质量

　　再看，（当m和n互质）只要x与m互质且x与n互质则x与m*n互质

　　任何与m互质的数x除以m的余数即（x%m）也必然与m互质，反之也如此

　　所以从（1...n）和（1...m）分别取x与n互质，y与m互质，则会唯一对应一个m*n中的值f 与m*n互质

　　而每个与（1...m*n）互质的值 f 都会唯一对应一个 （1...n）中与n互质的x和一个（1...m）中与m互质的y

　　所以phi(m*n) = phi(m) * phi(n)  ， (m，n互质)

　　证明完毕

那么这样，对于要求欧拉值的n，将他因数分解成  pi^ai, 而 phi(pi^ai )= pi^ai ( 1 - 1/pi )

再将pi相乘得到n，就可以得出公式      phi(n) = n* ∏ ( 1 - 1/pi )  

代码：

long long eular(long long n) {
    long long ans = n;
    for(int i = 2; i*i <= n; i++) {
        if(n % i == 0) {
            ans −= ans/i;
            while(n % i == 0)
                n /= i;
        }
    }
    if(n > 1)ans −= ans/n;
    return ans;
}

 从证明可以看出，欧拉函数是非完全积性函数

所以可以用线性筛来O(n) 预处理值

bool check[maxn];
int phi[maxn];
int prime[maxn];
int tot;//素数的个数
void phi_and_prime_table(int n) {
    memset(check,false,sizeof(check));
    phi[1] = 1;
    tot = 0;
    for(int i = 2; i <= n; i++) {
        if( !check[i] ) {
            prime[tot++] = i;
            phi[i] = i-1;
        }
        for(int j = 0; j < tot; j++) {
            if(i * prime[j] > n)break;
            check[i * prime[j]] = true;
            if( i % prime[j] == 0) {
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            } else {
                phi[i * prime[j]] = phi[i] * (prime[j] - 1);
            }
        }
    }
}

 性质：

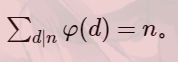
 考虑gcd，假设i与n的gcd为g，那么有g|n , gcd(n/g,i/g)=1