莫比乌斯函数

单点求解sqrt(n)  (可以自己改写，很简单)

int f[maxn],cc;
void solve(int n){
    cc=0;
    for(int i=2;i*i<=n;++i){
        if(n%i==0){
            while(n%i==0)
                f[++cc]=i,n/=i;
        }
    }
    if(n>1)f[++cc]=n;
}
int getmiu(int n){
    if(n==1)return 1;
    solve(n);
    for(int i=1;i<cc;++i)
        if(f[i]==f[i+1])return 0;
    return (cc&1)?-1:1;
}

筛法递推

bool vis[maxn];
int prim[maxn];
int mu[maxn];
int cnt;
void get_mu(int n) {
    mu[1]=1;
    for(int i=2; i<=n; i++) {
        if(!vis[i]) {
            prim[++cnt]=i;
            mu[i]=-1;
        }
        for(int j=1; j<=cnt && prim[j]*i<=n; j++) {
            vis[prim[j]*i]=1;
            if(i%prim[j]==0) break;
            else mu[i*prim[j]]=-mu[i];
        }
    }
}

解释一下线性筛

设a=x*x*y*y*z（x<y<z）

a仅会被x筛到

因为x*x*y*z在筛到素数x时就已经break了，同理x*x*y*y不会筛到z

因此，每个数仅被他的最小质因子筛到，因此为O(n)，这一性质也是可以利用的

 

解释一下莫比乌斯函数

由于每个数都是被它的最小质因子筛到

考虑一个数去除掉最小质因子，x=i*prim[j]

假如x是k个素数连乘,那么mu[x]=-mu[i]没毛病

假如x里有a*a

　　如果a是最小质因子，直接break掉，就等于数组初始值没毛病

　　如果a不是最小质因子，x的最小质因子是b，那么x/b的mu值已经处理好为0，那么mu[x]=-mu[x/b]也是没毛病的

 

性质  (copy的别人blog)

 

 

 对于性质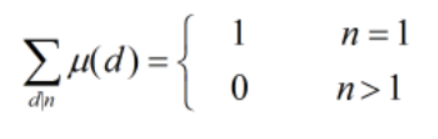莫比乌斯函数可用来容斥

发现对于n>1, sigma(mu(d), d|n) = C(n,0 )- C( n,1 )+ C(n,2) +.... + (-1)^(n) * C(n,n)  =  (1-1)^n  = 0

有p^2因子的莫比乌斯值是0，当然不用考虑

-C(n,2) 表示n的因子中，有C(n,2) 个素因子个数为2

因此这是一个容斥函数，所以才有了下面的莫比乌斯反演

莫比乌斯反演有两种形式，除了上面还有一种，对于两种形式用类似的方式可以理解一下