博弈论
资源汇总
① 视频资源:网易公开课频道 目前该站点汇集了大量的开放课程,内容丰富。
网易——耶鲁博弈论、网易耶鲁博弈论,字幕只到 16 讲,但优势在于随时可以播放,只要有网络随时可以观看,且没有广告人人影视开放课程——耶鲁博弈论上传此笔记时24 讲字幕已齐全,感觉这套字幕翻译质量很好,且保持了风格的统一,很适合学习的版本。且资源支持的下载方式多样,资源的健康程度也不错。我个人采用的即是这套资源。
资源包:
《策略与博弈论》作者:杜塔(含练习).Strategies_and_games-theory_and_practice(Dutta).pdf 英文版
课程所提到的影片:
《美丽心灵》拉塞尔·克劳和詹妮弗·康纳利搭档演绎约翰·纳什的一生,也就是本课程的核心概念纳什均衡的提出者。
《奇爱博士》库布里克三部曲之一,另外两部为《2001 太空漫游》《发条橙》《谍影重重三部曲》可以算是马特·戴蒙的代表作吧,本人最喜欢第三部。《特务风云》马特·戴蒙 Ben 的玩笑“耶鲁人都是间谍,间谍都是神经病。”《生活多美好 / 风云人物》 也就是 Ben说的《美丽人生》,也就是在第五讲最后的时候 Ben 介绍的那个挤兑问题。不过不是他说的银行而是 George Bailey(詹姆斯·斯图尔特 James Stewart)经营的“房屋贷款合作公司”,他为了大多数人的梦想放弃了自己的梦想……看到最后真的很令人感动。
《白雪公主》……就不上种子了,Ben 说“他们要是看了这部电影,喝咖啡时都不好意思说出来……”同时鉴于拉塞尔·克劳是我个人最欣赏的男演员之一,推荐他的几部,可以对比一下与《美丽心灵》中差异很大的人物塑造。
《角斗士》 《国家要案》 《洛城机密》 《三日危情》
第一讲 导论—五个入门结论
Introduction: five first lessons
本讲说是五个结论,但没有想象中的那么严肃,其中结论 4 更是在开玩笑。
策略形式:行为影响结果,然而结果不仅取决于你的行为,还取决于其他人的行为。
《策略与博弈》 普拉伊特·杜塔《策略》 乔尔·沃森
《战略思想》 Thinking Strategically Ben 强烈推荐中文有两个版本,一个是王则柯女儿翻的《策略思维》,另一个是我们学校董志强老师翻的《妙趣横生博弈论》,作为入门书籍的确很不错。
例:成绩博弈
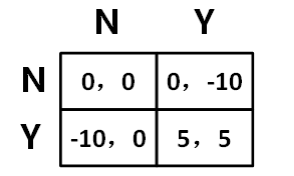
在你同桌不知道的前提下进行选择,若你选择 α,他选择 β,则你得 A,他得 C 若你们同时选择 α,则他们都得 B-;若你们同时选择 β,则你们都得 B+。
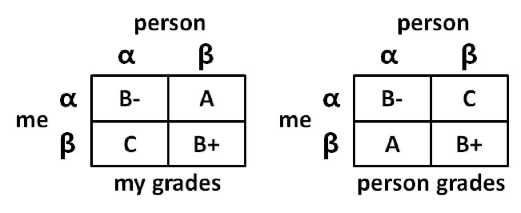
图 01-01 我方成绩 图 01-02 对手成绩
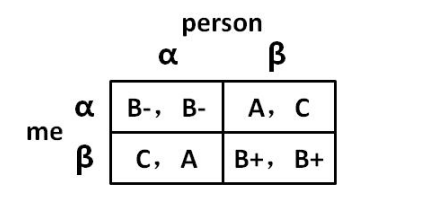
图 01-03
单元格内,第一位是我方的成绩,第二位是对手的成绩,包含游戏所有内容的矩阵
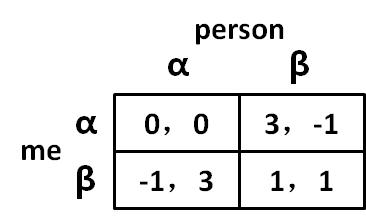
图 01-04
数字表示,代表效用或者功利,更直观的反应收益 A 代表 3 个单位效用,后面以此类推只关心自己的成绩的人——Evil gits 有的书译作恶棍不论对手作出什么选择,选择 α 的收益永远优于 β 当对手选择 α 时,选择 α—0 > 选择 β—-1 当对手选择 β 时,选择 α—3 > 选择 β—1如果 α 的结果严格优于 β,那么 α 相对于 β 是严格优势策略
结论 1:不选择严格劣势策略,原因是每次博弈会得到更好的收益。
本案例中人们不会选择劣势策略,反而选择优势策略,使总结果变得糟糕经济学 115,导致不充分的结果(Inefficient)即帕雷托效应公认的译法是帕累托效应,这里应该叫帕累托无效率,描述资源配置无法达到最优化的状态。
经典模型:囚徒的困境 A 认罪,B 不认罪,A 释放,B 判 5 年,反之亦然。都不认罪,各判 1 年,都认罪,各判 2 年。
结论 2:理性选择导致次优的结果。
Rational choices can lead to bad outcomes.
协商难以达成目的的原因不是缺少沟通,而是没有强制力。黑手党在书面协议不受保护的地方不断壮大,作为法律强制力的补充,维系所有合同不论是否合法。
Indignant Angel 愤怒天使
参看上一个收益矩阵
(A,C)我方获得 A 成绩,对手获得 C → 3 − 4 = −1 -4:负罪感导致的负向收益(C,A)我方获得 C 成绩,对手获得 A → −1 − 2 = −3-2:无法向父母解释这样的成绩
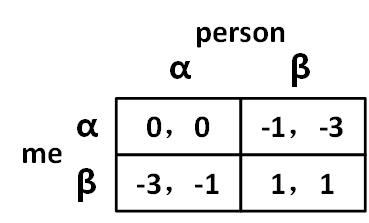
图 01-05
人们在乎的东西不同了,所以得到了完全不同的。协和谬误 协调问题(coordination problem),后续课程中会有更进一步讨论。
结论 3:汝欲得之,必先知之。
You can't get what you want , till you know what you want.
永远选择优势策略,选择非劣势策略,损失小,如果对手有优势策略则应以此作为选择策略的指导。
Evil gits VS. Indignant Angel
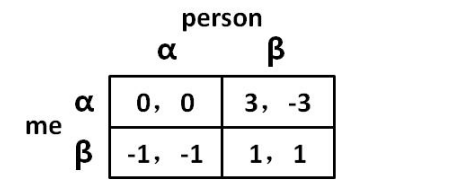
图 01-06
假设 me = Evil gits
Indignant Angel VS. Evil gits
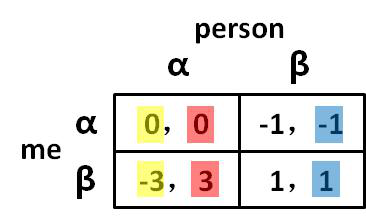
图 01-07
假设 me = Indignant Angel站在我放的角度分析没有优势策略当对手选择 α 时,我方选择 α—0 优于选择 β—-3当对手选择 β 时,我方选择 β—1 优于选择 α—-1
结论 4:耶鲁的学生很自私。
Yale students are evil.
换位思考
当我方选择 α 时,对手选择 α—0 优于选择 β—-1 第一行红色之于蓝色当我方选择 β 时,对手选择 α—3 优于选择 β—1 第二行红色之于蓝色不论我方选择 α 还是 β,对手选择 α,都是他的优势策略那么基于对手会选择优势策略的前提,选择我方的策略:
选择 α—0 优于选择 β—-3,即第一列的黄色
结论 5:站在别人的立场去分析他们会怎么做
Put yourself in other's shoes and try to figure out what they will do.
选数游戏:从 1 到 100 之间选择一个号码填到下面的方框内,不要让你的同桌看到,我们会计算全班的平均数,谁选的数字最接近平均数的 2/3,谁就是赢家。
第二讲 学会换位思考
Putting yourselves into other people'sshoes
开场提到的几个案例,囚徒困境的类似博弈:合作完成家庭作业,动机每个人都想偷懒价格竞争,两家企业都想削弱对方公共问题,公共资源的使用。
对于此问题的延伸可以参阅《博弈与策略》 P85 第七章 应用:公共问题如何才能形成博弈?
形成博弈要素:参与人(players),规定表述法 i 、j;
参与人的策略(strategies),规定表述法 、所有可能的策略集合 ,区别于参与人的策略 ,此处用大写 S 来表示,如上节课选数游戏中, = {1,2,3 … … 100}
某一次博弈 s,不带下标的小写 s 表示,称为策略组合(a strategy profile),也称策略向量、策略列表、策略剖面)
收益(payoffs) 取决于参与人 1 的策略一直到参与人 N 的策略,这些都是影响参与人 i 的的因素,当然也包括他自己的策略,记作( ,…… , …… )简写为 ( ) ,由策略组合决定(受所有参与人策略的影响)− 除了 i 外其他参与人每人的策略,因为有时候考虑在 和对手在不同选择下的收益是很有必要的。
选数游戏中以标准形式描述博弈: 5 美元 − 误差 ( ) = 0
用一个例子来熟悉使用符号语言来描述博弈
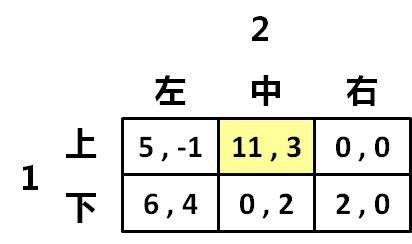
图 02-01
参与人:1,2
策略集合: S1 = { 上, 下 };S2 = 左, 中, 右
收益: U1 = 上, 中 = 11;U2 = 上, 中 = 3
严格优势策略定义:
参与人 i 的策略 ’严格劣于参与人 i 的另一个策略 ,在其他参与者选择 − 时,
选择 的收益 ( )严格优于此情况下 ’的收益 ( ’),对所有 − 均成立。

图 02-02
在防御者的角度没有优势策略,而站在攻击者——汉尼拔将军的角度存在优势策略,但并非严格优势,只是一个弱优势。



引用杜塔教授给出的定义
选数游戏:具体规则见第一讲
没有写下 common knowledge 和 mutual knowledge 的区别,这是很重要的一点
剔除[ 68,100 ],因为只有当所有人都选 100 时,100 的 2/3——66 又 2/3,才是个合理的答案。剔除劣势策略,剩余的选择[ 1,67 ],在这样的情况下,同理 [ 45,67 ] 也被剔除了。
[ 45,67 ] 策略在原博弈中并不是弱劣势的,可是一旦我们排除掉了[ 68,100 ],它们就成为了劣势策略,即弱劣势策略。
剔除[ 68,100 ],是一种直接思考;同时作为一个理性参与人的选择。
剔除[ 45,67 ],则是站在别人的角度去思考的结果,因为对手不会选择劣势策略。同时考虑到你的对手也是一个理性的参与人。
不断重复这个过程,最终会得到 1 的结果。
第三讲 迭代剔除和中位选民定理
Iterative deletion and the median-votertheorem
选举案例:
假设两个候选人,一系列政治主张中,共有 10 个立场,每个政治立场都有 10%的得票,且平均分布,选民会投票给离他们最近的候选人。
当你自己选择其中一个时,获得全票,对手和你同时选择时,你们两人均分选票,非选择区域靠近那个候选人,该候选人获得全票,若该区域与两个候选人等距,则选票均分。

举例如图 03-01,参与人 1 选择 2 号立场,赢得本立场的全部选票,同时 1 号立场选民将选票全都投给离他们最近的参与人 1,同理参与人 2 赢得了 4 到 10 号立场的全部选票,在 3 号立场上,两个参与人距离相等,均分选票。若两个参与人都选择 3 号立场,结果一致。
讨论: 1 立场劣于 2 立场
1(1,1) = 50% < 1(2,1) = 90%
括号内第一位为我方选择立场,第二位为对手立场; 1(1,1),我方选择 1 号立场,对方选择 1 号立场时,我方的收益;此处对比的是在对手选择 1 号立场时,我方选择 1 号立场与 2 号立场的区别。
1(1,2) = 10% < 1(2,2) = 50%
1(1,3) = 15% < 1(2,3) = 20%
1(1,4) = 20% < 1(2,4) = 25%
当选择立场>2 时,选择 1 号立场劣于选择 2 号立场,5%同理可证明 9 号立场严格优于 10 号立场
当对手选择 1 号立场时,对比我方选择 2 号、3 号立场的区别:
1(2,1) = 90% < 1(3,1) = 85%
当剔除劣势策略 1 立场和策略 10 立场,选择策略 3 立场严格优于策略 2 立场。
可自行论证当对手选择 2,3,……10 时我方选择 2 号、3 号立场的区别
按照以上方式迭代剔除劣势 2 和 9;3 和 8;4 和 7;最后只剩下 5 和 6 迭代剔除劣势策略 主旨在对立场的换位思考,推测对手的行为策略,同时想想对手会站在你的立场,反复此过程,最终结果往往会导致唯一的选择。
《策略与博弈》 P51-P52 正式的定义
预测结果是候选人会挤在 10 个立场中的中立地带,在政治学中这被称为中间选民定理。(Median Voter Theorem)也叫中间人投票定理,也可以通过偏好推导出来。
模型存在的问题:现实中选民并非均匀分布;选民常根据候选人的性格而非政治立场来进行投票,政治立场仅仅是单一维度;只适用于两个候选人的情况;同时存在弃权票;选民未必相信候选人所声明的立场。多维度在政治课程中有完善的模型,本课程不讨论。
“单一维度,非左即右”说到非左即右,更正式一点的说法是两难谬误,在此个人推荐一本书《学会提问——批判性思维指南(第七版)》,作者 M.Neil Brtuart Stuart M.Keele,中国轻工业出版社。严重同意!我认为此书是培养 critical thinking 的必读书
建立模型的目的:为了更好地描述事实激发灵感,模型由重要的事实抽象而来,逐步增加约束条件完善模型观察结果,比较分析结果的变化。
个人非常喜欢这个观点,和项目管理的 PDCA 循环一个道理,plan、do、check、action
最佳对策 Best Response
一般译作最优反应,相应动态博弈中先行者的策略是反应对应
施锡铨先生翻译的《策略与博弈》中采用的也是该译法,后文不再特别注释修订
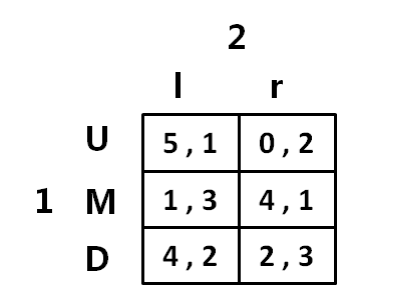
在这个博弈中不存在劣势,不要采用劣势策略和迭代剔除劣势策略的方法在此不适用
选择 U 是在对手选择 L 的 BR(最优反应)选择 M 是在对手选择 R 的 BR
对手的选择 L、R 等可能(1/2,1/2),我方的收益
U: 5 × 12 + 0 × 12 = 52
M: 1 × 12 + 4 × 12 = 52
D: 4 × 12 + 2 × 12 = 3
假设不等可能(2/3,1/3)重新进行预期收益计算,可自行运算。
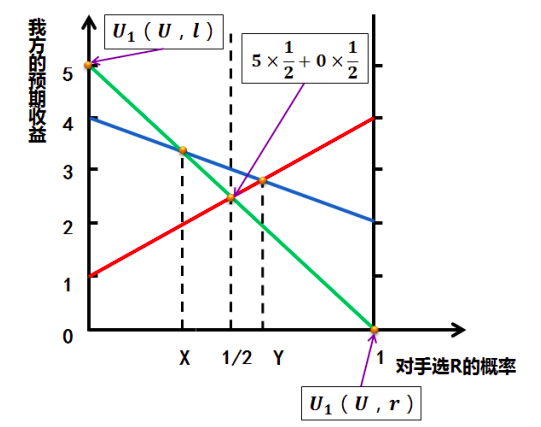
U M D
直线代表对手选 R 的不同概率上,我方的预期收益若对手选 R 的概率小于 X,选 U 若对手选 R 的概率大于 Y,选 M 若在 X、Y 之间则选择 D
X、Y 的解,每条直线可通过两点坐标建立直线方程,两直线联立即可得出交点坐标
解得:X=1/3
第四讲 足球比赛与商业合作之最优反应
Best responses in soccer and businesspartnerships
点球博弈:

4 代表进去的概率1 , = 4 向左射门,向左扑救,进去的概率为 40%使用第三讲同样的方式在平面直角坐标系中绘制图像

红线射手从左路射门的预期收益,绿线—右路,蓝线—中路
门将右扑救射手左射门仍有 90%的入射率,考虑 10%的射飞
对图形的分析,当守门员向有扑救的概率小于 1/2 时,BR 为向右射门,在上面的图形中可以看出从中路射门永远都不是 BR。
针对彩色线条的结论:不要选择任何信念下都非最优反应的策略,即蓝色线条,在任何区间内都不是最优反应PS:此模型忽略右脚习惯
力量提高带来精准性的降低 向中央射门反倒成为最优选择
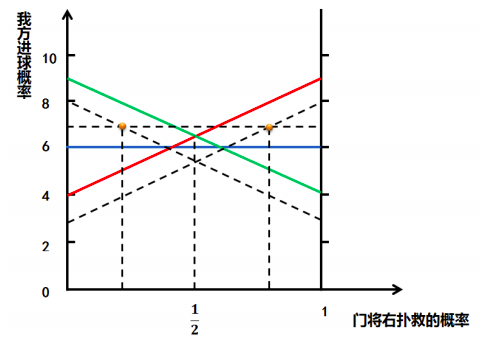
大力射门出现的概率变化 8—3;3—8;7—7如虚线位置中间三角形区域对应的 X 轴区间中(即两个橘黄点间的范围)射为最优反应
最优反应参与人针对对手策略的定义:


实际上就是用 VNM 效用函数进行比较
冯·诺依曼—摩根斯坦(Von Neumann and Morgenstern)效用函数 见《策略与博弈》 P21
预期收益,此案例中,在参与人 i 持有信念 p 的情况下,他选择左路攻门的预期收益等于,门将扑向左路的概率乘以两人都选择左路下,参与人 i 的收益,在加上门将扑向右路的概率乘以门将扑向右路参与人 i 左路进攻时,参与人 i 的收益。

合伙人博弈:
两个参与人都是公司股东,各持有公司 50%的股份,供应合伙关系;每个股东要选择对公司投入精力,以“小时”表示,策略集合 Si=[0,4],即可选择0 到 4 间任意实数“小时”的投入,这是一个连续区间,不是同于选数游戏中的只能选整数。

同理可得
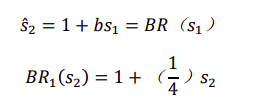
根据s2的定义域(策略集合)[0,4],绘制参与人 1 在s2情况下的 BR,即红线同理可得参与人 2 在s1情况下的 BR,即蓝线
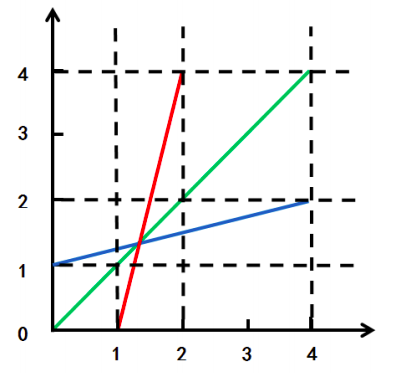
[0,1) U (2,4]永远不会成为参与人 1 的最优反应,基于参与人不会选择劣势策略,剔除区域如下图。
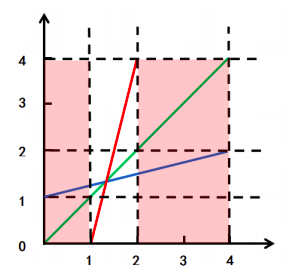
同理剔除参与人 2 的非最优反应,剔除区域如图
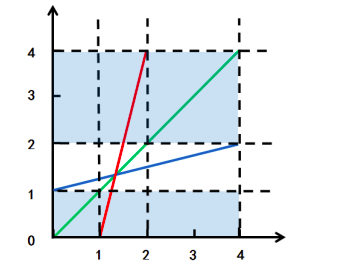
取两个剔除区域的交集,剩下就只有中间的一小块区域
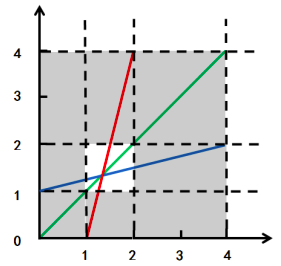
将这块小区域进行放大,如图 04-08
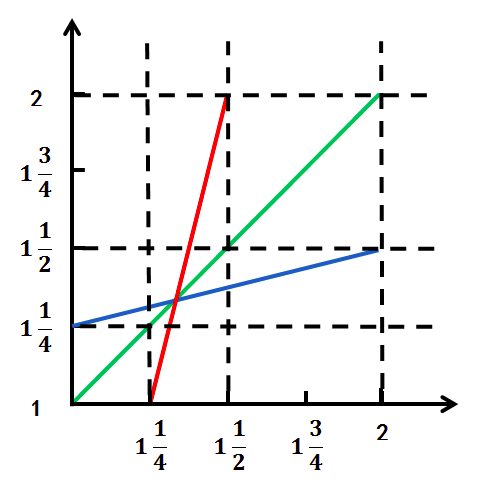
新生成的图像除了点坐标不同外和初始图像完全一样,再次剔除非最优反应,迭代剔除最终将归为一点。
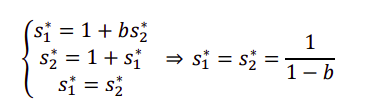
此处介绍的边际收益与边际成本,鉴于本课程第六讲:古诺的双寡头模型中会涉及该知识,我个人将在第六讲的笔记中补充一部分经济学的知识。
存在外部性(externality)
上图中的交点即是著名的纳什均衡点,在此处参与人们都采用了自己的最优反应。
第五讲 纳什均衡之坏风气与银行挤兑
Nash equilibrium: bad fashion and bankruns
纳什均衡定义:
策略组合是一个集合,该集合包含每个参与人的一个已选策略,用 1∗, 2∗,…… ∗ 表示,纳什均衡(简写为 NE—Nash Equilibrium),是满足下列条件的策略组合,对于任意一个此集合内的参与人 i ,她所选择的策略 ∗是其它参与人所选择策略的最优反应,其它参与人的策略用 −∗ 表示。
应该是最优反应,定义不能有问题啊,简单地说 NE 是一组策略,其中每个 player 所选的策略都是对其他 player 所选策略的最优反应
学习 NE 的动机:不为当时做出的决定后悔,因为已经采取了最优反应。
应该是各个 player 选择 NE 的动机;同样重要的一点是 NE 是自我实现的(self-fulfilling/self-enforcing)任何参与人都严格不会改变策略,改变策略严格不会使参与人获得增益。其他参与人不改变行为的前提下,自己改变行为并没有任何好处。

找出最优反应:

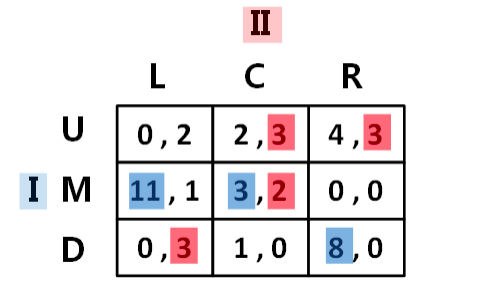
NE = (M,C)
NE 与优劣的联系:
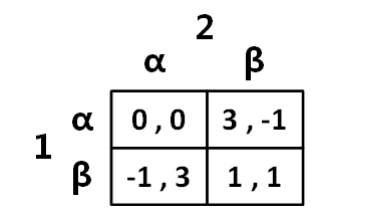
α 严格优于 β
NE = ( α ,α )
严格劣势永远不是最优反应,最优反应才可以出现 NE。
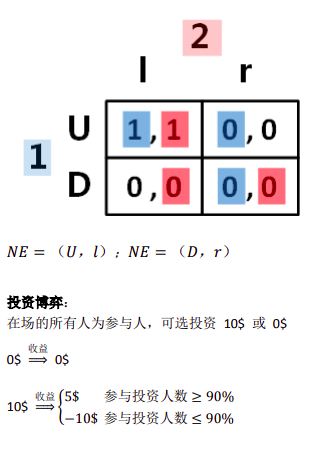
博弈会朝着趋向于一个均衡的方向自然发展,结果(self-enforcing)不断趋向一个NE。
寻找 NE 的一个有效方法是猜想与验证(guess and check)较劣的不投资均衡相当于较优的 NE 处于帕累托劣势协调之所以能达成在于他不同于囚徒困境,它没有去说服人们采取一个严格劣势策略。
协调博弈 coordination game 协调谬误
《美丽人生》 a wonderful life 吉米·斯图尔特 Jimmy Stewart 说服人们达成一种较优的 NE,电影种子见资源包
第六讲 纳什均衡之约会游戏与古诺模型
Nash equilibrium: dating and Cournot Going to the movies
B:The Bourne Ultimatum 谍影重重
G:The Good Shepherd 特工风云
S:Snow White and the Seven Dwarfs 白雪公主
“但我课不觉得现代的女性四处游荡,等待你的白马王子出现是个好策略。”
If you are doing that strategy, take it from a Brit, most princes are as dumb as toast, not worth waiting for.
如果你真的采取这个策略,记住这句英国的俗语吧,王子和土司一样蠢,不值得你去等的。
女方想去看《谍影重重》-B,而男方则倾向于《特工风云》-G,双方谁都不像去看《白雪公主》-S,同时他们都希望两个人能一起去观影,否则没有收益。“如果两个人协调好一起去看《白雪公主》,你喝咖啡时都不好意思提这事。”
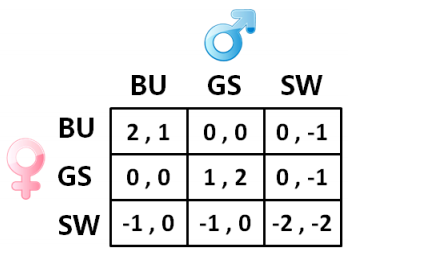
S 对两个人皆为劣势决策,剔除
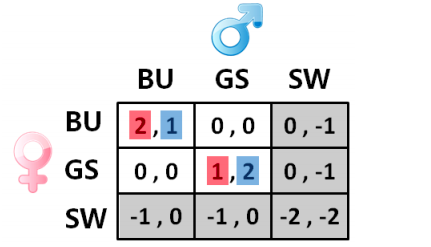
𝑁𝐸 = (𝐵𝑈,𝐵𝑈);𝑁𝐸 = (𝐺𝑆,𝐺𝑆)
不同之处,上一讲的博弈只是协调博弈,无利益冲突
性别大战( Battle Of The Sexes)
古诺的双寡头模型(Cournot Duopoly)
《策略与博弈》 P69
参与人:两家公司;
策略:某种同质产品产量, 1, 2分别表示两家公司的策略;成本计算 c × ,c 为生产一个单位产品的成本;
市场定价的两个参数 a,b
价格 p = a − b ( 1 + 2 ) 两家企业生产的越多,该产品的市场价格也就越低;

收益:
𝑈1(𝑞1,𝑞2) = 𝑝 × 𝑞1 − 𝑐𝑞1 收入—成本
将价格表达式带入上式:
𝑈1(𝑞1,𝑞2) = 𝑎𝑞1 − 𝑏𝑞1 2 − 𝑏𝑞1𝑞2 − 𝑐𝑞1

此时是公司 1 对公司 2 产量(0)的最优反应,即垄断产量
完善价格与产量图像
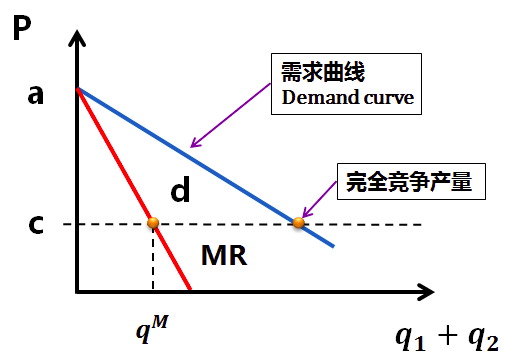
完全竞争产量,需求曲线与边际成本的交点,此时价格等于成本,当一家公司的产量达到该点时,另一家公司的 BR 就是停产,否则会使产品的价格低于成本价。垄断产量,边际收益与边际成本的交点,即点 d
本打算在 v_2.0 里讨论一下边际收益等于边际成本时利润最大的问题,但后来查了一下百度文库和智库的相关条目,解释的非常清晰,此处本人不再注解,给出几个链接供非经济专业且有兴趣的读者深化理解。

公司 2 每种产出下公司 1 的最优反应,令𝑞1 ∗ = 𝑞2 ∗
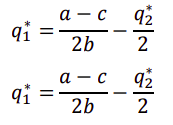
解得:
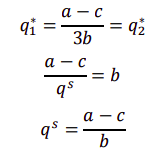
边际成本与需求曲线的交点,完全竞争产量
古诺在纳什出生前 100 多年即解出该博弈的答案
古诺博弈不同于第五讲中的合伙人曲线,合伙人曲线是向上倾斜的
这不是一个策略互补博弈,而是一个策略替代博弈
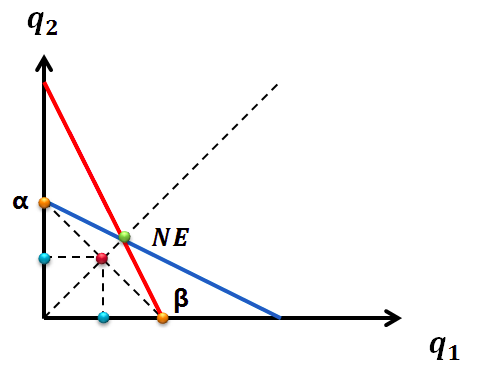
垄断产量使行业利润最大化,两点如上图 α,β 两点连线的中点(红色的点)所分别对应的产量(水蓝色的点),各生产一半亦可实现行业利润最大化,问题签订这样的限产协议是违法的,私下达成协议仍然存在问题。
一方会根据另一方的产量,如下图所示公司 1 根据公司 2 的 A 点的产量(通过协议达成的结果——垄断产量的一半),选择本公司最优反应曲线(红线)所对应的产量——C 点

同样公司 2 会根据公司 1 的 C 点产量,来选择在本公司最优反应曲线(蓝线)所对应的产量。 此处就不作图了
一方违约增产造成另一方同样根据对方产量依照最优反应曲线来生产产品,反复迭代无限逼近纳什均衡,因此通过私下协议来维持垄断产量是很困难的,因为缺乏强制力,双方都有违约的动机。
完全竞争产量 > 古诺产量 > 垄断产量 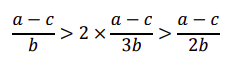
除了产量还有价格的比较:完全竞争价格 < 古诺价格 < 垄断价格
第七讲:纳什均衡之伯川德模型与选民投票
Nash equilibrium: shopping, standing andvoting on a line
伯川德竞争 (Bertrand competition)
古诺是产量上的竞争,伯川德则是在价格上的竞争
参与人:生产相同的产品的两个公司成本是固定的边际成本,生产 1 个单位产品消耗成本 c
策略:定价,本例中用 1代表公司 1 的价格,用 2代表公司 2 的价格,注意此处不同于前面课程用 s 来表示参与人的策略每个公司可以把价格设定在 0 ≤ ≤ 1 ;即为前面课程的策略集合设定价格根据需要来调整产量
产量的制定: Q(p ) = 1 − p 为两家公司定价较低的价格公司 1 产品的需求量
注意:现实并非完全符合以上的表达式,为了便于研究对于模型做了很多强制性假设来简化
收益: 𝑞1 × 𝑝1 − 𝑞1 × 𝑐 = 𝑞1( 𝑝1 − 𝑐 )
为了找到 NE,首先要找到公司 1 的 BR,是关于公司 2 价格的函数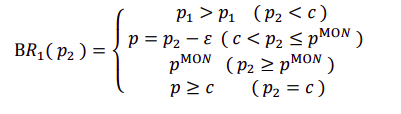
分段函数:
第一段,公司 2 定价低于成本价销售时,公司 1 定价必须高于 2才能避免销售每件产品都亏损,同时也意味着产品没有销量——退出市场。
第二段,当公司 2 的定价高于成本时,公司 1 只需要比该价格低一点点,用 来表示,即可占领市场。且应当低于垄断价格,因为垄断价格才是最大利润。
第三段,当公司 2 的价格高于垄断价格时,公司 1 选择垄断价格。
第四段,当公司 2 的价格等于边际成本时,公司 1 选择大于或等于边际成本
𝑁𝐸 = ( 𝑝1 = 𝑐,𝑝2 = 𝑐 )
这个结果与完全竞争非常相似,尽管只有两家公司。这个结果叫做伯川德悖论(Bertrand Paradox)
与上次相同的设置,但不同的策略集合设定,得到一个完全不同的结果。
此处把完善模型作为了作业留给学生去完成了。
线性城市模型(Linear city model)
一个路贯穿城市,两个公司分别坐落在 0、1 点,消费者 y 到公司 1 的距离为 y,到公司 2 的距离为 1-y,假设每个消费者买且只买一个产品。消费者会选择对他而言总成本最小的
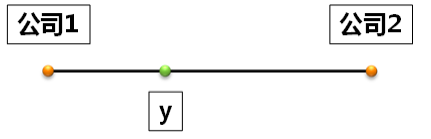
例如:在 y 点的消费者,如果从公司 1 购买则他们支付 1 + 2,产品的价格 1,和交通成本 2;到公司 2 购买则需要支付 1 + (1 − )2,交通成本以距离的平方的速率增长。
作业为解出公司针对每一个其可能设定的价格,它的需求是什么,并找到所有的纳什均衡。
候选人选民模型(Candidate-Voter model)
假设选民在线上平均分布,选票的获得与第三讲中一致,与该模型的区别:①候选人的数目不固定;②候选人不能选择他们的立场;假设每个选民是一个潜在的候选人
参与人:选民
策略:是否参选(选民将选票给与最近的候选人,得票最多者当选,平局掷硬币)收益:获胜赢得奖励 B,参选付出成本 C,且 B>2C;若选民不参选获胜者的立场距离该选民越远,则该选民将承受越重的负面效应,若该选民在线上 X 点,获胜者在 Y 点,则承担−| − |的成本,两点间距离的负向效应,也就是对方当选后给未参选的选民造成郁闷程度。
例如:三种可能的情况
①Mr.x 参选并获胜,他的收益为 B − C
②Mr.x 参选,但 Mr.y 获胜,Mr.x 的收益−𝐶 − |𝑋 − 𝑌|
③Mr.x 不参选,但 Mr.y 获胜,Mr.x 的收益为−|𝑋 − 𝑌|
假设 = 2$ ; = 1$ ;选民为 17 人,每一个立场的价值为 (1/17 )$
图形类似第三讲的图形,不过立场变为了 17 个
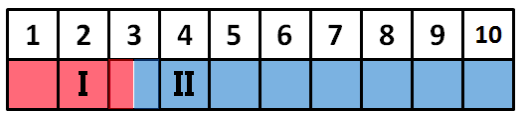
假设位于中间的选民参选,那么对于其他任何一个选民来说再参选都不是一个 NE 均衡,因为相对于第二个参选的选民不参选都是更好的收益。相当于 Mr.x 的②③两种情况的对比。
如果非中心点的选民参选,同样也不是个 NE,因为中心点的选民参选相对于不参选而言成为了他的优势策略。
假设依照上图分析,两个对称点的选民参选,如 4 号和 7 号,那么 1、2、3 号和 8、9、10 参选将使一个劣势策略,因为他不仅不会当选,且会分掉离自己更近的候选人选票,从而把当选者推向离自己更远的立场。
第八讲:纳什均衡之立场选择、种族隔离与策略随机化
Nash equilibrium: location, segregationand randomization
继续上一讲的候选人模型
结论 1:此模型可能存在多个 NE
并非所有均衡中的候选人都保持中间立场
结论 2:如果左派有一个新的候选人加入,可能会导致右派获胜的概率增大,反之亦然。
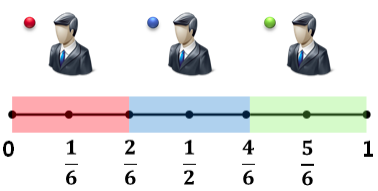
三个候选人分别处于 1/6 立场,1/2 立场和 5/6 立场,此时每人当选的概率为 1/3,此时若左派的候选人稍微向 1/6 右侧靠近一点,右派的候选人稍微向 5/6 左侧靠近一点,那么中间立场候选人的选票就会被这两个候选人分掉一小部分,从而使中间候选人被排挤掉。
结论 3:如果候选人太极端就会有新的中间候选人参选。
选址模型(Location model)
假设两个小镇,东镇和西镇;世界仅有两种人,高个和矮个;每种人都有 10 万,每个城镇都只能容纳 10 万人;参与人:高个、矮个策略:选择东镇还是西镇
如果城镇只有参与人是矮个,其他人都是高个,那么参与人的收益为 0,反之亦然;如果是高个和矮个混居,数量都是城镇人口的一半则收益达到最大;如果城镇全是矮个或高个则收益是最大值的一半。
人们可以自由选择想要居住的城镇,如果选择一个城镇的数量超过了容积,则会从所有选择该城镇的参与人中随机抽取,分配到另一个城镇。
例如有 15 万人选择东镇,那么每个人只有 2/3 的概率可以住在这里,另外随机抽取 5 万人,会被分配到西镇去。

①两个 NE 是种族隔离;一个 NE 是每个城镇中不同人种均匀分布;两者皆为严格均衡,后者稳定性差,“弱均衡”这三种情况下参与人都无法通过改变策略来取得更高的收益
②临界点(Tipping Point)
③另一个不太现实的均衡,所有人都选择同一个城镇而被随机分配
结论:
·看上去毫无意义的博弈规则,有时是很重要的条件。
·社会随机分配,其结果要比所谓的自主选择要好。
结论:
①模型中种族隔离的结果,不能作为人们喜欢种族隔离的论据。
②随机分配(randomization);校车现象(bussing)
③可以通过自下而上的方式实现随机分配。
每个人都通过抛硬币的方式来决定去那个镇子,选址模型的另一个 NE。
抛硬币的不确定性,引入混合策略(Mixed strategies),在这之前接触的都是可选的纯策略。
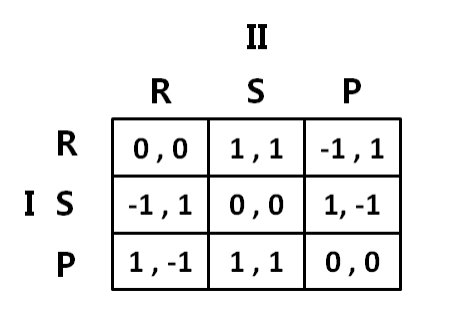
猜拳博弈
在纯策略(pure)中没有 NE NE 按 1/3 概率选择混合策略

第九讲:混合策略定义及其在网球比赛中的应用
Mixed strategies in theory and tennis
混合策略用 表示, i 表示参与人, 表示采用每个纯策略的概率
用 ( ) 表示在混合策略 下,参与人 i 采用 的概率,即 ( )是 赋予
纯策略 的概率。
例如:上一讲中的猜拳博弈,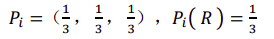
可以将纯策略看做是一个特殊的混合策略,即赋予某个策略的概率为 1;
混合策略的收益:
混合策略 的预期收益,每个纯策略预期收益的加权平均数

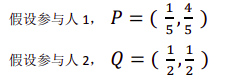
计算预期收益: 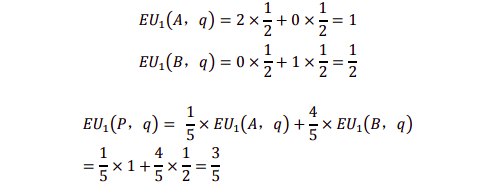
结论:如果一个混合策略是 BR,那么混合策略中的每个纯策略必须也是 BR,也就是说它们的收益必须相同。
定义:一个混合策略( 1∗, 2∗,…… ∗ ),是一个混合策略 NE,当且仅当对任意参与人 i ,在面对 −∗ 时他的混合策略 ∗,是该参与人的 BR。
含义:如果 ∗ 中某个纯策略被赋予正概率,那么该策略本身是一个 BR。
网球博弈:
参与人:Venus Williams and Serena Williams
策略:Venus 可以选择把球打到对手的左侧(反手),或是右侧(正手)收益矩阵如下
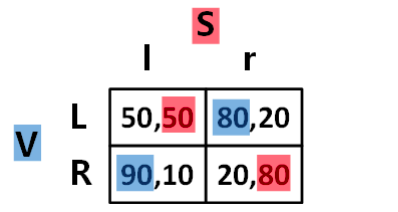
例如: 1( , ) Venus 将球打向对手的左侧,而对手判断失误,采取了向右的预判,那么 Venus 得分的机会为 80%,而对手防守得分的机会为 20%。
假设 Serena 右手截击的水平高于左手。不存在纯策略的 NE,寻找混合策略的 NE。
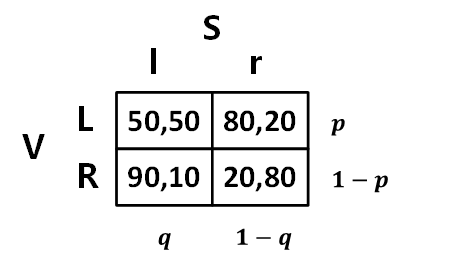
首先来找到 Serena 的 NE 混合策略( ,1 − ),为此需要分析 Venus 的收益
Venus 面对 Serena 采取 ( ,1 − ) 时的收益
L:50 × + 80 × (1 − q) ①
R:90 × + 20 × (1 − q) ②
如果 Venus 的混合策略属于 NE,那么选 L 和 R 的收益一定相等,进而预期收益一定相等。
联立 ①② 解得: = 0.6 Serena NE
通过 Venus 收益求出的 Serena 的混合策略,既然知道了 Venus 也采取混合策略,那么我就可以令 Venus 的两种收益相等。
然后计算 Venus 的混合策略
找到 Serena 的 NE 混合策略 ,1 − ,为此需要分析 Serena 的收益
Serena 的收益
l:50 ×q + 10 × (1 − p ) ①
r:20 ×q + 80 × (1 − p) ②
联立 ①② 解得:p = 0.7
NE = [ 0.7,0.3 ,( 0.6,0.4 ) ]
如果 Serena 防左的概率大于 0.6,那么 Venus 的 BR 是把球打向右侧如果 Serena 防左的概率小于 0.6,那么 Venus 的 BR 是把球打向左侧
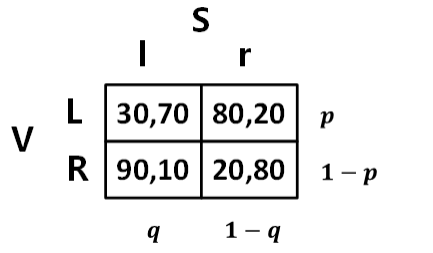
新教练改善了,Serena 打反手球的水平导致的结果:① 直接影响 提高 ② 间接影响、战略影响 降低使用解得 q相同的方式解得新的均衡 q ′ = 0.5
结果证明,间接影响的作用更大使用解得 相同的方式解得新的均衡 p′ = 7/12 < 7/10
《策略与博弈》中考虑混合策略的意义理由 1:混合策略可能优于一些纯策略(这些纯策略本身并不劣于其他纯策略)。P101 理由 2 混合策略的最差情况可能好于所有纯策略的最差情况。P103理由 3:如果我们只限于纯策略,那么,我们也许不能找到博弈的纳什均衡。P104
第十讲 混合战略棒球,约会和支付您的税
Mixed strategies in baseball, dating and paying your taxes
验证上一讲混合策略
p∗ = 0.7
q∗ = 0.6
是否是 BR
Venus 面混合策略 ∗是 Serena 的混合策略 ∗的 BR
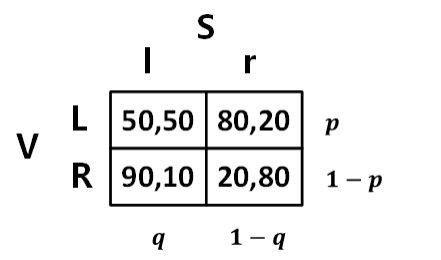
Venus 的收益:
Venus 在对手采取( 0.6,0.4 ) 的混合策略下纯策略的收益分别是L:
𝑈𝑉[ L,( 0.6,0.4 )] = 50 × 0.6 + 80 × 0.4 = 62
R:𝑈𝑉(R,(0.6,0.4 )] = 90 × 0.6 + 20 × 0.4 = 62
Venus 采取 ∗的混合策略的收益:
𝑈𝑉[ ( 𝑝∗,1 − 𝑝∗ ),(0.6,0.4 ) ]= 0.7 × 62 + 0.3 × 62 = 62
Venus 不存在改变纯策略的严格有利改变,她任何一个纯策略的收益都与混合策略∗的收益相等。
证明混合策略不存在严格优于 ∗的混合策略,回忆一下上一讲混合策略收益的定义,纯策略、加权平均数
结论:只需要考虑改变纯策略是否严格有利即可。
因为就混合策略本身的定义来说就不会有严格有利的混合策略偏离,两个相同的数怎么加权都是一样的。
apple picking 摘苹果
Yale Rep and see play 耶鲁剧院去看戏
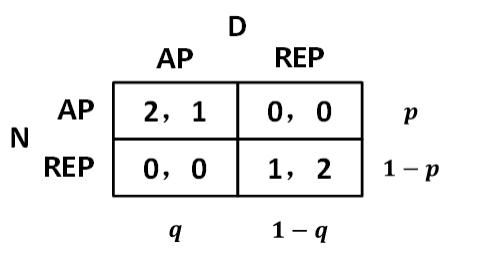
两个纯策略 NE (AP,AP) (REP,REP)
性别大战混合策略下的均衡找出 NE 通过 Nina 的收益来求出 David 的策略
𝑈𝑁 [ AP, (q,1 −q)] = 2 ×q + 0 × (1 −q ) = 2q①
𝑈𝑁 [ REP,(q,1 −q)] = 0 × q+ 1 × (1 − q) = 1 − q②
联立①② 解得:
q= 1/3;1 −q = 2/3
同理解得:
p= 2/3;1 −p = 1/3
证明 BR 与威廉姆斯姐妹网球博弈的证明方式一致,且该处比较完整。
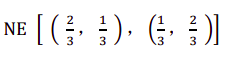
人们并不是完全随机化的,可以把混合策略看成处于均衡时人们的某些信念。
税收检查:
参与人:纳税人 tax payer;审计员 auditor
策略:如实申报 honestly;隐瞒申报 cheat
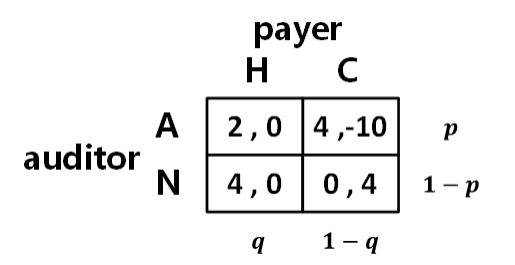
审计员的收益:
最好的结果,不审查而纳税人如实申报,收益为 4;抓到漏税收益也为 4;最糟的结果,不审查,但纳税人逃税成功,收益为 0;审查而纳税人如实申报,因为审查是有成本的,因此收益为 2;
纳税人的收益:
瞒报被查出巨大损失-10,逃税成功收益为 4。
纯策略不存在 NE,寻找混合策略的 NE
通过审计员的收益来求得纳税人的策略 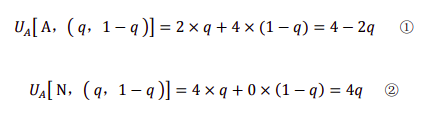
联立①② 解得: q = 2/3
同理通过纳税人的收益来求得审计员的策略,解得: = 2 / 7
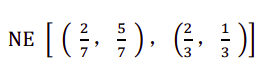
政策试验,提高惩罚,从-10 增加到-20
审计员的收益等式为发生变化,因为他的收益没有变化,也就是说纳税意愿对他是
否选择审计检查无影响。q = 2/3
纳税人的收益:对均衡纳税意愿有影响,决定着纳税人的混合策略是审计员的收益,不改变审计员的收益,当然也就不会改变纳税人的均衡混合策略。
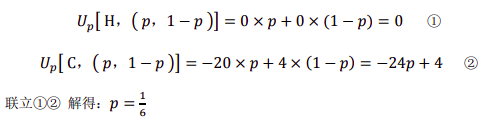
提高对逃税的惩罚并没有提高纳税人的纳税意愿,却降低了审计员的审计概率
1/6 < 2/7
举例:提高逃税的收益,将导致审计概率的提高,因此商学院高收入的教授反而拥有更高的纳税意愿,因为较高的审计概率的存在。
联邦审查率的设计更多的去审查富人,这并不是说明穷人更诚实而富人更。
鉴于国会意愿属于富人阶层,让国会议员获得制定审查率的权利是不明智的,他们可能会报有其他政治目的而非提高税务系统的整体效率。
本讲有两个重点要补充:
1.关于混合策略的三种解释:
(1)某个 player 随机化 ta 的策略
(2)某个 player 对另一个人采取某种策略的概率估计
(3)群体中特定参与人的比例
2.求混合策略的方法:
(1)设某个 player 采取某个策略的概率,通过令另一个 player 的收益无差异来求这个概率
(2)在给定另一个 player 的混合策略下,对某个 player 的收益函数求一阶条件可以求得另一个 player 的混合策略
(3)无论用上述何种方法,最好算出来了检验一下是否有偏离该混合策略的激励,计算上只需要检验纯策略
第十一讲 进化稳定:合作,突变,与平衡
Evolutionary stability: cooperation, mutation, and equilibrium
进化论 (Evolution)
① 博弈论对生物学的重大影响,尤其在动物行为学中把基因看成策略,把遗传适应性当做收益,好的策略使种群不断壮大,即有适合基因的个体会繁衍,带有不适合基因的个体会灭绝。
将动物的行为(策略)看做是天生,而不是自由选择 ② 生物学尤其是进化生物学,对社会科学产生了重大影响
一个经济学案例:
假设市场中存在这样的公司,这些公司并不关心什么策略能最大化利润,什么策略能尽可能降低成本,它们可能毫无科学根据地选择策略,在竞争激励的市场环境下,只有那些成本较低但利润颇丰适应环境的公司才能得以生存下来。
简单的回忆一下高中生物知识,基因突变是不定向的,而自然选择则是定向的。基因(DNA),存在于细胞核,通过 RNA 将自身的片段输出到细胞核以外,以其上的编码来指导蛋白质合成,从而控制干细胞的功能细胞,形成组织器官,构造生物体。
比如长颈鹿的脖子,可能这个物种最初没有这种特征,但在种群当中极小的一部分个体发生了基因突变,这个突变是不定向性,也就是说可能出现蹄子大的,腿长的,大耳朵的等等。而这个物种的普遍的生存环境下,赖以为生的植物很高大,此时那些脖子长的个体则有更多的机会填饱肚子。
低矮的空间内有更多的竞争者,那么个体分得食物量将受到限制,而在高处则只有这部分数量极少长颈的个体在分享着食物,充足的食物意味着这部分个体的平均体魄比其他非长颈的更好,那么在与天敌或其他致命危险对抗时,这部分的存活几率会更高,基因在种群中的比例也就会逐渐提高,
而这种优势是可以通过遗传给予后代的,随着时间的推移,原来的突变少数成了种群中的大多数,最后完全淘汰那些短颈个体。这并不是说蹄子大的,腿长的,大耳朵的变异没有用,只是说在这个环境中长颈更占优。而环境是自然形成的,它赋予了某些突变基因生存的优势。这也就是自然的定向选择。
公司倒闭和基因灭绝道理是类似的。
简化模型,专注于种内竞争,通过双人对称博弈来进行研究,很大的种群,采取的策略与生俱来,对其进行随机配对。即采取相对成功策略的个体数量会增长,相反则会减少。不存在基因的重新分配。
合作 cooperate 背叛 defect
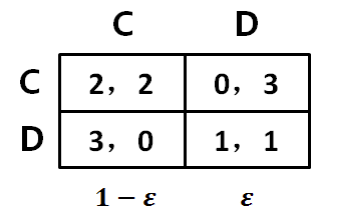
合作是否是一个稳定策略?假设有1 − * 的蚂蚁都是合作型


②>① → C 相对于 D 不是进化稳定策略 (Evolutionarily Stable),简写为 ES背叛的个体在种群所占的比例会逐步提升,直至全部种群皆为背叛个体背叛是否是一个 ES?做一次反向试验来进行验证

假设有1 − 的蚂蚁都是背叛型

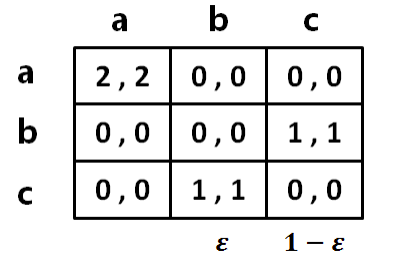
ES?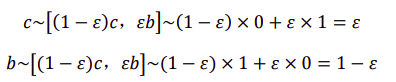
b 本身不是 ES,同时 c 也不是 ES
如果策略 s 或者( s , s )不是 NE,那么策略 S 就不是 ES。即如果 s 是进化 ES,那么( s , s )一定是 ES。
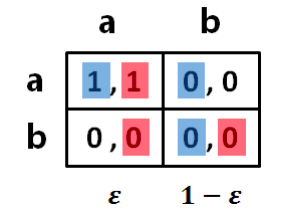
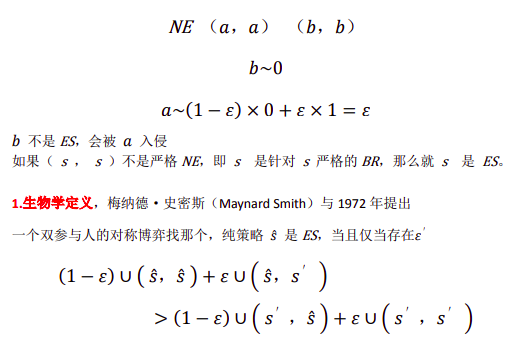
对任意 s′ 都成立,对任意 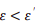 都成立。
都成立。

第十二讲 进化稳定:社会公约,侵略,和周期
Evolutionary stability: social convention, aggression, and cycles
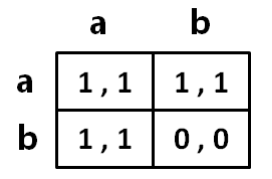
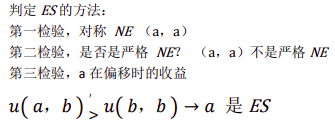
社会传统的进化 (evolution of social convention )
靠左行车还是靠右行车

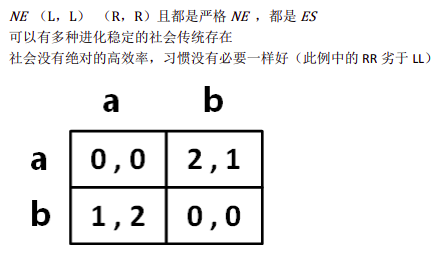
类似性别大战( Battle Of The Sexes)的收益矩阵
a 使用攻击性策略,不会躲避,b 仁慈性策略,在相撞前会规避一个著名的例子就是 Chicken Game 叫做斗鸡博弈或胆小鬼博弈《策略与博弈》 P33 鹰—鸽 博弈 (强硬—懦弱)NE (b,a) (a,b)
此博弈中不存在对称纯策略 NE ,需要考虑混合策略
混合策略下的性别大战的
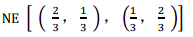
见第十讲 摘苹果和看戏剧
单型(Monomorphic):只有一个形态或一个类型——单型种群多态(polymorphic)——混合型种群
策略 是混合策略 ES
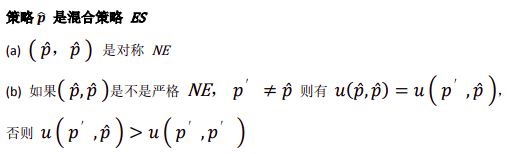
混合策略偏离 比如 (2/3 ,1/3) 换为 (1/3 ,2/3)那么结果和混合策略相同,a 的个体突变相对于混合策略结果与混合策略本身的结果
是一样的。所以在混合策略的 NE 里不可能是严格的。
为保证 ES,检验是否满足(b),

对所有可能的混合
变化p′
for all mixed mutations p′
此处做个一个简单的讨论而没有去使用严格的数学证明,但它已经足够了。
自然界中混合均衡的两个解释
① 基因本身是随机的
② 稳定混合也意味着在 ES 中,以这种比例稳定存在海象的例子 SLF (sneaky little) 鹰—鸽之争 Hawk and Dove
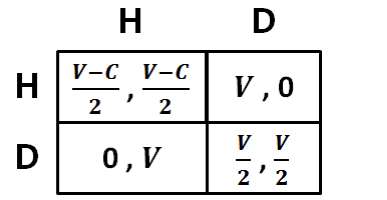
奖励 V > 0 战利品
代价 C > 0
D 是一个进化稳定策略(ESS,Evolutionarily Stable Strategy)吗?
第一部检验,NE (D,D)? 不是 NE,所以不是 ESS
H 是 ESS?
第一部检验,NE (H,H)?

检查鸽派对鹰派的收益
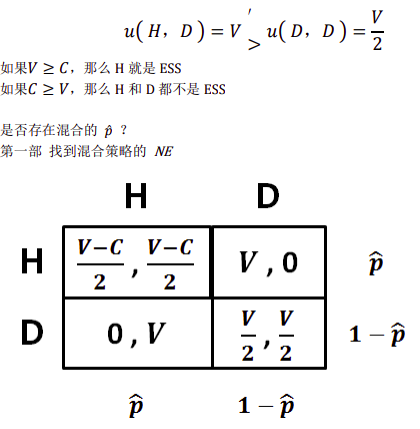


在这个例子中没有 ESS
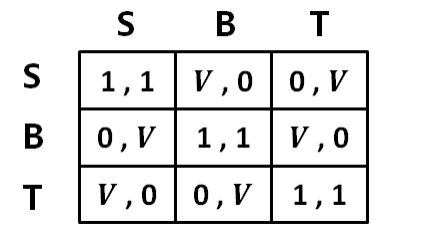
三色蜥蜴例子,解释循环维持平衡的过程
印象没错的话,高中生物教材称它为生态平衡,只不过这个概念更为广泛不是在博弈模型中的单纯种内,而是同时考虑种间、外界环境等内容。
第十三讲 序贯博弈:道德风险,激励和饥饿的狮子
Sequential games: moral hazard, incentives, and hungry lions
帽子里的钱 (Cash in a hat)
关于这个游戏的说明请认真听,具体描述请对应下面的树形图(《策略与博弈》中叫展开型,这个名词个人感觉更为恰当)。
树形图只是一个笼统的说法,它可以指决策树又可以指博弈树,前者在决策论使用,后者在博弈论中使用,结构相似但决策论跟博弈论不是一回事。
extensive 也有种译法叫扩展式,跟策略式相对,张维迎的书也有写,都是翻译不同而已。
序贯博弈 (Sequential games)
参与人 2 在作出决定之前知道参与人 1 的决策,且参与人 1 知道这种情况。
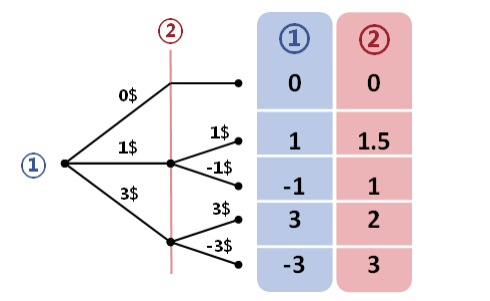
个人绘图说明,在本树形图中(请注意与 Ben 的方式略有不同): 1)中间节点没有对每个节点标明参与人 2 可以在此做出选择,而是以一条与参与人2 颜色相同的直线了表明在此处他可以进行策略选择; 2)为节省空间最上面的分支不再采用相同的斜率延伸到与终点处于相同水平位置后写出结果,而是用水平直线来进行延伸; 3)在所有分支中节点都有黑色圆点,无节点则此处不提供策略选择,但遵照上一条会对该处进行水平延伸,以使得所有结果都在一个水平位置方便比较; 4)对于分枝的决策不是画箭头表示,而是直接将该分枝变换颜色,同时加粗线条;后续的所有树形图,除特殊情况,皆以该方式绘制。希望如此能易于阅读。
关键问题是作出预测 (anticipation)
沿着树形图向下看,站在后行动参与人的立场上思考,看下级参与人会有什么动机,找到他们的 BR,再根据树形图倒回来。
即向树的分枝看,然后在回到树的主干上来。
记得 Thinking Strategically 这本书上对逆向归纳法有个很好的说法:looking forward,thinking backward
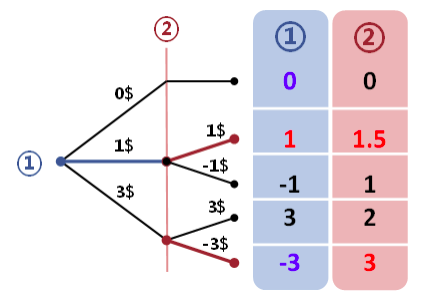
实例说明:
1.收益站在参与人 2 的角度做出判断,上分枝参与人 2 没有选择权,无需分析;中分枝,1.5 相对 1 是优势;下分枝,3 相对 2 是优势;参与人 2 的分枝选择已用红褐色标出。未标出可以认为已经作为劣势策略被剔除。
2.逆向推进一层站在参与人 1 的角度,可以选择的三个策略分别对应的结果为:0、1、-3。找到参与人 1 的优势决策。
以上方法的名称——逆向归纳(BI,backward induction)
希望得到一个更好的结果,某种动机却阻止我们达成更好的结局,称之为道德风险(moral hazard)。
典型的道德风险
选择限制项目的规模,或者说贷款额度,通过降低规模来降低被骗的风险。
改变 ① 3$ ② 3$ 分枝的收益分配,有原来的(3,2)变为(1.9,3.1)
激励设计(incentive design)
动机不是上天赋予人们的,它是由合同双方设计出来的。
“有时大蛋糕的一小块,可能比小蛋糕的一大块要大。”
担保 (collateral)
担保的作用在于,它降低了你不偿还贷款的收益。但却使你过的更好了,因为它改变了其他人的行为,这对你却是有益的。
AD 1066 征服者威廉 登陆英格兰参与人:
诺曼底公爵威廉率领的侵略者 Norman 哈罗德率领的撒克逊防御者 Saxon
可选策略:战斗 (Fighting) 逃跑 (Running Away)
威廉的初始策略:破釜沉舟(Burn);留条后路(Not Burn)

此处将选择策略的颜色换成了更为鲜明的色彩,上面那个图比较小还好,这个图使用柔和的色彩确实差一些了,与参与人相近的鲜艳色彩表明参与人的选择。最后一个层级的策略与前一层相同上分枝为 F。
承诺 (commitment)
减少可选策略而改变其他人的行为,改变不了其他人的行为则毫无意义。
《奇爱博士》 Dr. Strangelove 斯坦利·库布里克 Stanley Kubrick“必须要让对手知道。”
节点(Node) 终点(End Node) 连线(edge) 路径(path)

5 号狮子知道没有来自后方的威胁,于是准备放心大胆的吃掉 4 号狮子;
4 号狮子知道背后有个虎视眈眈的家伙,于是只能对着美餐流口水;
3 号狮子预料到 4 号狮子的顾忌,于是悠闲的等着享用 2 号狮子;
2 号狮子不想让 3 号狮子得逞,只能忍饥挨饿;
1 号狮子:“我吃了绵羊还是首领!”
绵羊:“为什么狮子得数量不是偶数。”
第十四讲 逆向归纳:承诺,间谍,和先行者优势
Backward induction: commitment, spies, and first-mover advantages

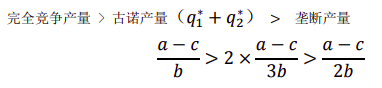
对于古诺博弈的详细讨论见 第六讲
斯塔克伯格 (Stackelberg)
厂家 2 已经知道 q1,需要选择 q2
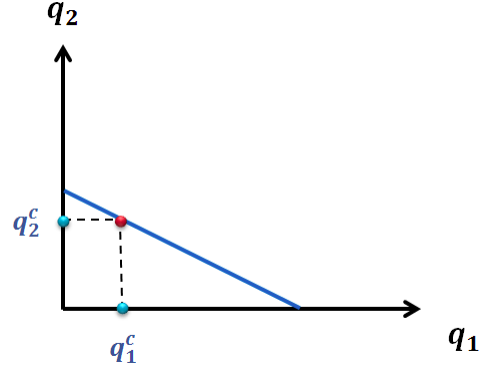
厂家 2 针对 q1,按照 BR 曲线,选择与之对应能最大化厂家 2 利益的 q2;
101
厂家 1 知道了这个q 2,又会根据它来调整自己的最优反应——产量 q1,于是厂
家 2 再根据这个 q1′,再决定出 q2′,从而无休止的继续下去。
第一部的思考,站在厂家 1 的角度,它知道任何选择都会导致厂家 2 作出依照规律的相应选择。
策略代换 (Strategic Substitutes)
厂家 1 增产,厂家 2 就作出减产来回应 1 ↑,B 2 1 ↓
在斯塔克伯格模型,厂家 1 不需要知道厂家 2 的产量也能有理由超过古诺产量继续生产,因为这可以迫使对手减产,对厂家 1 是有利的。
厂家 1 的利润一定会上涨市场上的总量 1 + 2 的影响
根据图像,q 2每减产 1 个单位, q1的增产量多余 1 个单位
此处简单解释一下:


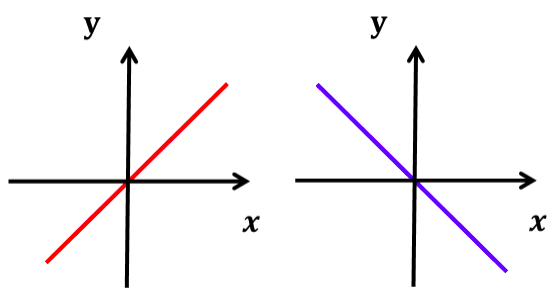
例如左侧的图中直线方程为y = x 此时斜率为tan45°,而右侧直线方程为y = −x,此时斜率为tan135°,此时两个斜率的角度值互为补角。一直觉着在博弈论中说到斜率就很别扭,在此特别注释一下。
斜率问题已经说过,经济学指绝对值,算弹性的时候也一样
这是我外行的一个例证,这个错误就保留下来给非经济类专业的读者做个提醒吧,同时还想说一下 Ben 的博弈论讲的确实很易懂,即便对于非经济专业的听众。
( q1 + q2) ↑ ,P ↓,厂家 2 的利润下降;
消费剩余(CS,consumer surplus)↑
数学证明:
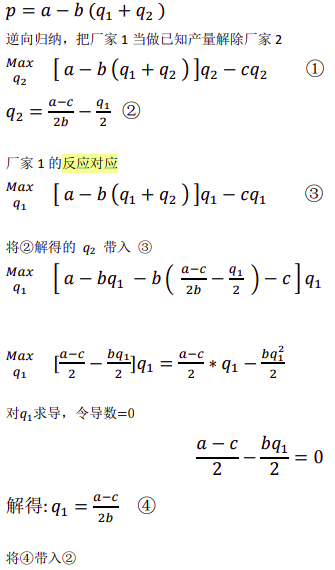

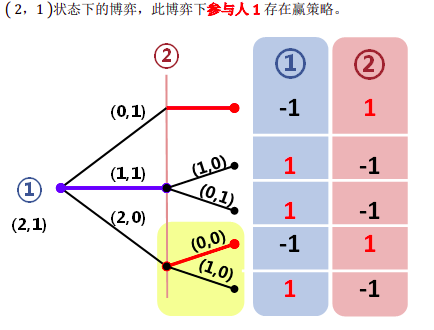
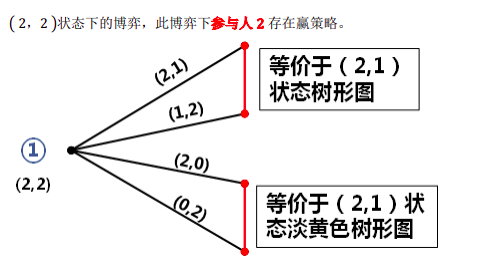
需要注意的时上面的两个分支在连接( 2,1) 状态下的博弈树图时需要改一下参与人顺序。而其他任何的状态都可以想象为这两种状态的推广。
“在双方都会玩 NIM 时,永远不要让自己在两堆相等的时候获得选择权。”
第十五讲 逆向归纳:国际象棋,战略和可信的威胁
Backward induction: chess, strategies, and credible threats
策梅洛定理(Zermelo theorem)
两个参与人,完全信息博弈,博弈有限节数
三个结果参与人
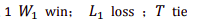
参与人 1 有赢策略,不论参与人 2 如何应对
参与人 1 有平局策略,不论参与人 2 如何应对
参与人 2 有赢策略,不论参与人 1 如何应对
此处 NIM 拿子游戏见第十四讲最后的树形图
使用归纳的方法证明(by induction)
把博弈的最大长度用 N 来表示,要在博弈的最大长度上进行归纳证明。
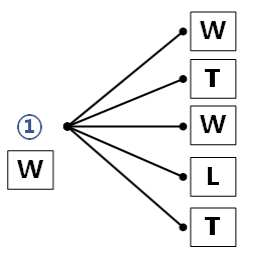
用优势的末节点取代起点假设这个命题对所有这样的博弈,在长度为 N 时都成立正确的字幕是 path≤N
证明所有的长度为N + 1的博弈也都成立
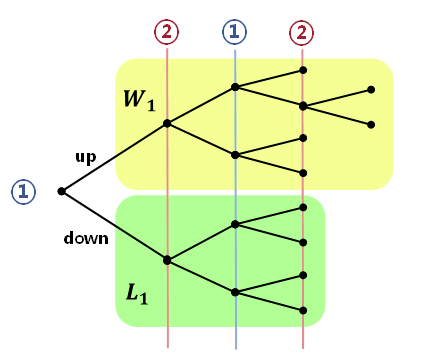
N = 3
N + 1 = 4
子博弈——博弈中的博弈,淡黄色(长度为 3)、淡绿色(长度为 2)的两个区域分别是两个子博弈。
根据归纳假设(induction hypothesis),此博弈(长度为 3 的博弈)有解。假设其解为 W;长度为 2 的博弈有解,假设其解为 L。
上面的博弈可以被转化为:
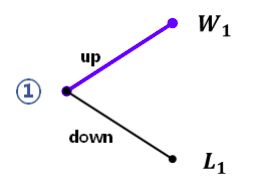
这是一个长度为 1 的博弈,有解。
如果长度为 N 或更少的博弈有解,那么长度为 N+1 的博弈有解。
Marienbad
石子阵列,N 行 M 列,可供选择的策略,被选中的点,其左、上的所有石子被拿走。如图若选中蓝色的点,淡黄色区域内被移除。参与人交替进行选择,拿到最后一个字的人输

作业:证明,根据策梅洛定理,无论 N、M 等于多少,此博弈都有解
完全信息博弈 (games of perfect information)
在任意一个节点上或者说每个节点上被轮中的参与者,都知道自己处在真个博弈的哪个节点的博弈。这也暗示着,参与者知道如何到达该节点。
纯策略,在一个完全信息博弈里,参与人 1 的纯策略,它是一个完整的行动计划,这个纯策略明确了参与人 1 将要在每个节点上采取怎样的行动。
例如:

这个树形图绘制不采用前面树形图的方式,否则反而不易观察了。后面的简单树形图,同样采用此方法,目的都是方面阅读。
参与人 2 策略:[ l ] [ r ]
笔记存在的问题敬请指正 By Apollo QQ:77981960 Gabriel QQ:460323397
参与人 1 策略:[ 𝑈,𝑢 ] [ 𝑈,𝑑 ] [ 𝐷,𝑢 ] [ 𝑈,𝑑 ] BI [ (𝐷,𝑑),𝑟 ]

NE [ (D,d ,r ] [ (D,u) ,r ]
NE 和 BI 无法对应,机械地寻找博弈中的 NE,会发现采取的行动很不明智。
另一个例子:
Ent 公司可以选择是否进入 Inc 公司的行业,Inc 可以选择是否发动对 Ent 的反击。


NE (i𝑛,N𝐹) (ou𝑡,𝐹)
BI (i𝑛,N𝐹) 不应该相信那个生成会反击的人真的就会反击。 (ou𝑡,𝐹) 建立在一个不足信的威胁基础上。
第十六讲 逆向归纳:声誉和决斗
Backward induction: reputation and duels
继续第十五讲最后的例子
加入一些条件,一个公司,处于垄断地位,垄断了十个不同的市场,假如它们有顺序性,垄断者会对第一个尝试进入者发起攻击,从而威慑后面观望者,对于最后一个市场垄断者不会发起进攻,因为没有建立威慑的动机了。
因为不可能去阻止第十个尝试进入者,所以第九个尝试进入者就成了最后一个,逆向归纳所有人都该进入市场。
即使有 (1%)的概率垄断者是疯狂的,他就可以用疯狂的名义吓退进入者。
即使在十个市场都处于垄断地位,人们也会进入并与之竞争,连锁店博弈(the Chain
Store Paradox)。
决斗(Duel)
扔海绵
Pi( d ) 参与人 i 在 d 点击中对手的概率
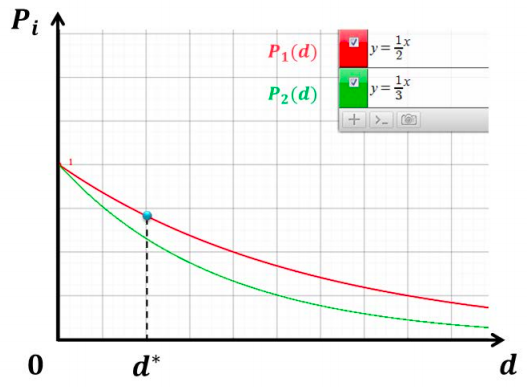
此处用 chome 应用 http://graph.tk/ 生成了一个类似图像,用的是 1/2 和 1/3 的指数函数,图中的两个方程除了用于生成图像,无其他用途。
预先抢投是一个关键点
优势定论 Dominance Argument 和 BI
A 假设还没有人投出,如果 i 选手知道假设在 d 点 j 选手不会投出,下一轮他就会更近一步,此时 i 选手不会投出。
B 如果 i 选手在 d 点知道 j 选手会在 − 1 点投出,那么他应该投出海绵。
当前轮次的命中率要大于对手在下一轮次的失误率,如此比较是因为当前赢得游戏的概率是击中对手的概率,在下一轮次前进一步赢得游戏的概率取决于下一轮次对手失误的概率。(获胜率之间的比较)
前提是满足 如果 i 选手在 d 点的命中率 ≥ j 选手下一轮在 − 1 点的失误率,则应当投出。

此处得出结论是使用“优势定论 ”的结果,或者按照前几讲说法,剔除劣势策略,占优可解
d∗ 处的矛盾, i 选手无法确定 j 选手是否会投掷,因此无法确定自己的策略。
逆向归纳的推导
d = 0 时 Pi( d ) = 1 → 第一次投掷应该发生在 d∗ 处
有时等待是个好策略。Sometimes waiting is a good strategy.
不要过度自信,也不要迷信先下手为强。
第十七讲 逆向归纳:最后通牒和讨价还价
Backward induction: ultimatums and bargaining
参与人 1,参与人 2
参与人1 向参与人2 给出一个分享1 美元的条件,参与人1 获得S,参与人2 获得1 − S,记作 S,1 − S 。
参与人 2 有两个选择,接受则按 S,S − 1 分配,拒绝 0,0
即使在非常简单的游戏中,使用逆向归纳的时候也必须小心。在现实世界当中,人们除了明显的收益还会关心其他东西。
两期议价博弈 (two period bargaining)
一阶段:1 美元,参与人 1 向参与人 2 给出条件, 1,1 − 1 。
参与人 2 有两个选择,接受则按 1,1 − 1 分配,拒绝则进入二阶段。二阶段:参与人 2 向参与人 1 给出条件 2,1 − 2 参与人 1 有两个选择,接受则按 2,1 − 2 分配,拒绝 0,0
每轮会有一个折损(discounting)—— < 1; 可以假设 = 0.9 带入理解一下
此处讲的一个折现问题,考虑了资金的时间价值,经济上常用于投资方案比选,将不同时期的资金流入与流出折现到一点来进行分析,这也就是财务净现值。 例如:今年的 100 元,在银行存款年利率为 10%的情况下,选择存款,明年将获得 100 元的本金,10 元的利息。也就是说考虑资金的时间价值,明年的 110 元也就相当于今年的 100 元——100 元就是明年 110 元的现值。
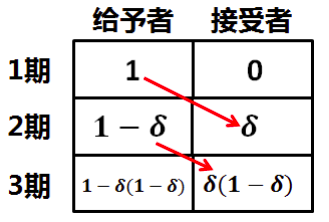
网友 Gabriel 在此处的解释相当明白了
给予者、接受者:这里的 offerer 指首先出价的人(这里是 player1),receiver 则指接受价格的人(这里是 player2)。
1-3 期:指 n 期博弈的结果
1 期的 0:若 player 2 拒绝了 player 1 的出价则 ta 将一无所有,因此即使 player 1 提
出(1,0)的分配方案 ta 也会接受
2 期的 δ:如果 2 拒绝了 player 1 的出价,那么到第二轮 ta 将会提出(0,1)的方案并且 player 1 会接受,因此 player 1 会将 1 贴现到今天的值 δ 留给 2,并且双方都接受((1 − δ , ))的出价。下面 n 期的推理都用相同的逆向归纳法进行
分析这类问题时总是假定:在 player 1 提出的价格与 player 2 在下一期得到的价值贴现到本期的值两者相等时,player 2 会接受 player 1 的出价。
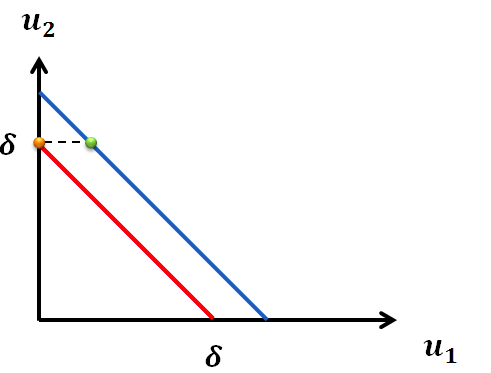
两期博弈中参与人 1 向参与人 2 给出的条件(淡绿色点),参与人 2 获得 美元,参与人 1 获得1 − 美元。
如果参与人 1 给与参与人 2 > 1 × 参与人 2 会接受
如果参与人 1 给与参与人 2 < 1 × 参与人 2 会拒绝
如果参与人 2 知道明天可以得到 1 美元,那么参与人 1 今天至少要分给参与人 2 美元。
我个人理解在此处已经和最初的分钱案例不同了,但 Ben 似乎没有做一个明确的转换,此处参与人 1 给出一个参与人 2 一定接受的价格。
其实是一样的,单纯的扩展到无限期讨价还价而已,不是不同的案例
类似上面我举的存款例子,全部的待分金钱是明天的 110 元,参与人 2 明天得到 110 他是可以满意的,因为他占有了全部,那么在利率为 10%的情况下,今天的拿到 100 元实际也就等于明天到自己选择的时候占有了全部。
三期博弈 逐步走向一个议价模型 (alternate offer bargaining)
10 期博弈 收益
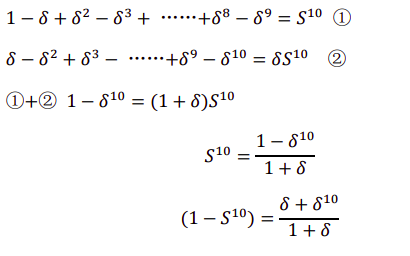
如果参与人 2 在第 1 轮拒绝了提议,参与人 2 在第 2 轮给出他的条件,那么就要在第 3 轮博弈中给出条件,我们证实了在第 2 轮博弈中,即如果参与人 2 在第 1 轮博弈中拒绝了条件,他会在第 2 轮中给出条件,那么在第 2 轮中他能够得到1 − 𝛿,所以你需要在第 1 轮给他 (1 −𝛿 )
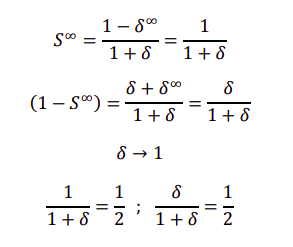
总结:
(1)轮流提议的议价过程,在特殊条件下,会得到平均分配,这需要满足三个条件。
① 可能会出现无穷次议价
② 𝛿→ 1 可视为无折损
③ 有相同的折损原因 𝛿1 = 𝛿2 (分析在折损率不同的情况下的结果)
(2)快速给出的提议被接受,没有议价环节
第十八讲 不完全信息:信息集和子博弈完美
Imperfect information: information sets and sub-game perfection

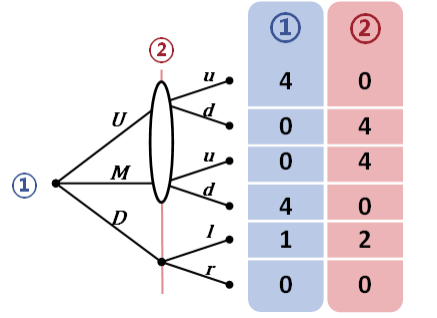
信息集合(information set)
《策略与博弈》中以一个椭圆型来表示信息集合,这和数学上所用的表示法是一致的,且更易于理解,但为了作图的方便并和课程保持一致后续仍然会使用虚线。
参与人 2 不能分辨处于信息集合中的两个节点,参与人 2 可以区别参与人 1 是选了上中,还是选了下,但无法区别上或中。
定义:信息集合
参与人 i 的信息集合是一系列参与人 i 无法识别的参与人 i 的节点。
对信息集合的规定:
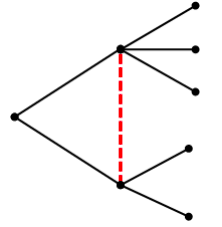
·参与人 2 可以通过观察选择的数量来判断他所处的节点
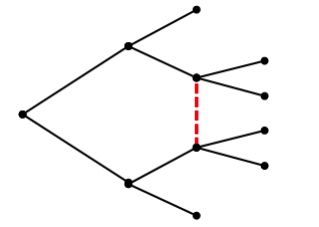
·参与人 1 可以通过第一选择判断他所处的节点
定义:完全信息博弈(perfect information)
这里 Ben 跟很多书一样只讨论完全且完美信息的博弈,也就是说每个 player 对博弈的历史阶段都有完美记忆(perfect recall)
树上所有的信息集合都只包含一个节点的博弈。
不完全信息博弈(imperfect information)
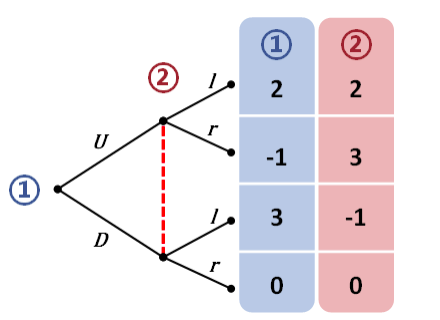
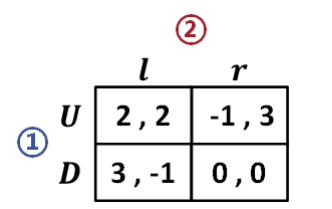
定义:纯策略(pure strategies)
参与人 i 的纯策略是一个完全的行动计划,它告诉参与人 i 在他的每一个信息集合一定要如何行动。

由上面的树形图可以转化为如下矩阵
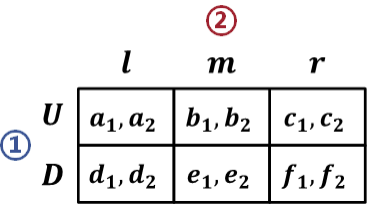
由上面的矩阵可以转化为如下的树形图

博弈的关键是信息,而不是时序。

参与人 1 的策略:𝑈𝑢,𝑈𝑑,𝐷𝑢,𝐷𝑑
参与人 2 的策略:𝑙,r
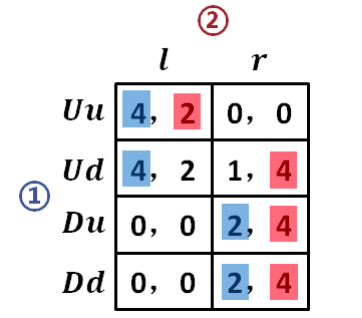
NE ( 𝑈𝑢,𝑙 ) ( 𝐷𝑢,𝑙 ) ( 𝐷𝑑,𝑟 )
BI ( 𝐷𝑑,𝑟 )

三人博弈,阐述纳什均衡的问题
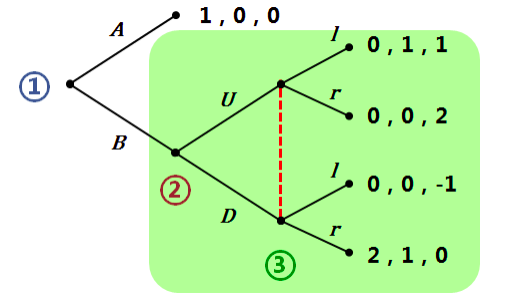
NE ( 𝐴,𝑈,𝑙 ) 但这个均衡并不可信

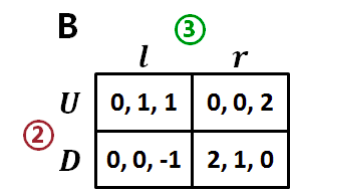
只考虑参与人 2 和参与人 3 的博弈,子博弈——淡绿色部分
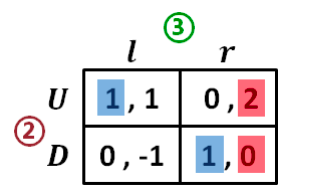
在整个博弈中 ( 𝐴,𝑈,𝑙 ) 是一个 NE ,但这个均衡标明在进入子博弈时无法达到 均衡,因此这个均衡是不可信的。
子博弈(sub-game):
子博弈是博弈的一部分,它满足以下三个条件。
① 子博弈必须从单个节点开始
② 它包含该节点的所有后代节点
③它不能破坏任何信息集合
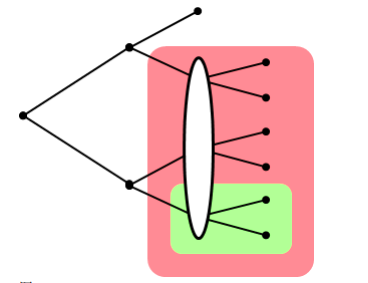
再次使用一下《策略与博弈》中的绘图方式,这种绘图方式对信息集合的表达让人更明白子博弈满足条件的第三条。
淡绿色区域不能成为子博弈是因为它破坏了信息集合——那个白色的椭圆。淡红色区域不能成为子博弈是因为它不是从单个节点开始。
如果 (S1∗, S2∗,… … Sm∗ ) 它们能在任意一个子博弈中达到 NE,那它就是一个子博
弈完美均衡(SPE,sub-game perfect equilibrium)。
子博弈精炼 NE 的一个重要特点是它可以排除不可信的威胁要成为 SPE,本身必须是一个 NE。
SPE (B,D ,r)
第十九讲 子博弈精炼均衡:招商引资和战略投资
Subgame perfect equilibrium: matchmaking and strategic investments
别搞砸了(don't screw up)
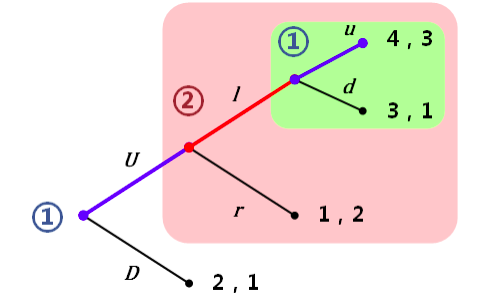
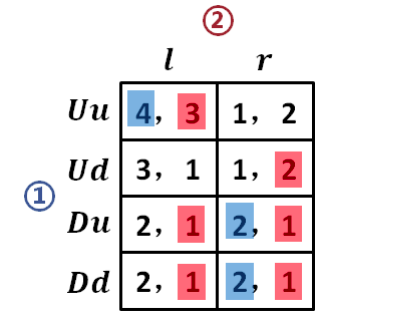
NE ( 𝑈𝑢,𝑙 ) ( 𝐷𝑢,𝑟 ) ( 𝐷𝑑,𝑟 )
BI ( 𝑈𝑢,𝑙 )
子博弈精炼(sub-game perfect)

图中淡绿色的子博弈 NE
源自策略的定义,它告诉每个参与人在不同信息集合下应该如何行动,即是有些博弈中信息集合无法获得,策略仍然为参与人在当前状况下提供指示。
根据整体矩阵得出的纳什均衡指示 NE ( 𝑈𝑢, 𝑙 ) ( 𝐷𝑢, 𝑟 ) ( 𝐷𝑑, 𝑟 )
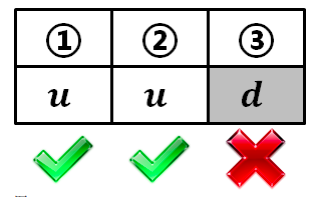
用子博弈的纳什均衡去符合整体博弈的纳什均衡,排除不符合的部分。子博弈精炼均衡要求,每个子博弈必须满足 NE
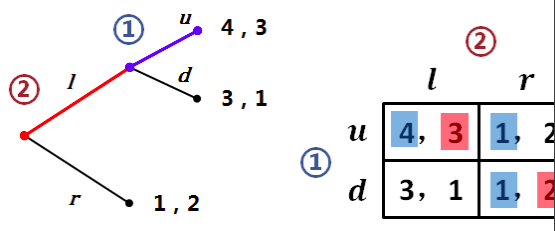
图中淡红色的子博弈 NE (u, l)(d,r)
根据整体矩阵得出的纳什均衡指示 NE (Uu,l)(Du ,r)(Dd ,r)
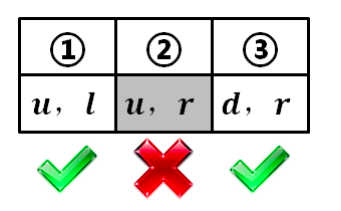
②在子博弈中非 NE 排除
两次排除后剩下的唯一一个子博弈精炼均衡 SPE(Uu,l) ,符合 BI。
介绍人博弈 (Matchmaker game)
大卫倾向加迪斯的《冷战》Dave Gaddis Cold War 妮娜倾向斯宾塞的《中国》Nina Spence China
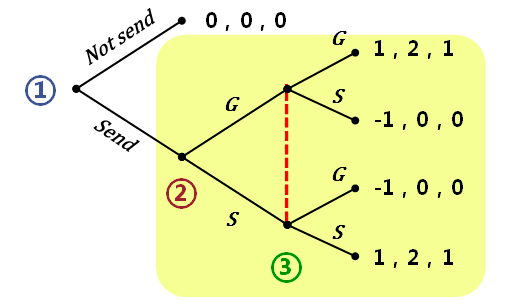
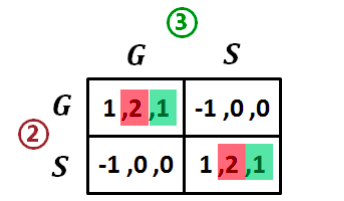
纯策略的 NE (G,G)(S ,S) 两者都为参与人 1 带来 1 个单位的收益
整体博弈 SPE= (sen ,G ,G )(send,S ,S)
站在参与人 1 的角度 1 的收益相对于 0 是优势策略
性别大战中混合策略的 NE
NE [(2/3 ,1/3 ),( 1/3 ,2/3)]
参与人 1 撮合参与人 2 和参与人 3,他们碰面的概率 2/3 × 1/3 + 1/3 × 2/3 = 4/9
参与人 1 撮合时均衡中的预期收益是 4/9 × 1 + 5/9 × (−1) = − 1/9
站在参与人 1 的角度 0 的收益相对于− 1/9 是优势策略,他应该选择不撮合
SPE= (no sen , mi , mi)
博弈共有 3 个 SPE,每个都对应子博弈中的一个 NE
投资案例
原方案是年产 1 百万吨,使用新设备节约0.5$/吨,1 百万吨就是节约 50 万
购置设备 70 万,70 万>50 万,因此不该租用设备。
(2)经济学的答案 Economic
假设自己垄断,那么产量应遵照边际收益等于边际成本——此讨论见第六讲,见下图
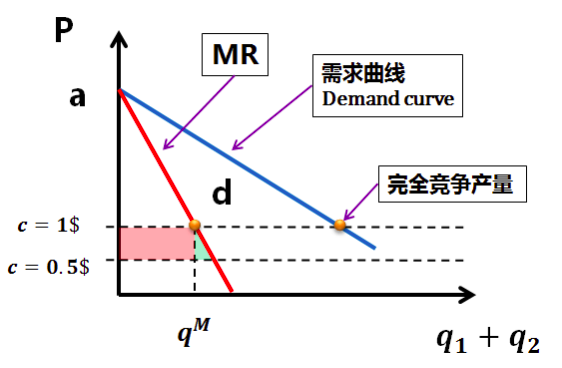
红色矩形部分即为会计师的答案,他们忽略了因为成本的降低,厂家会调整自己的产量,即绿色三角形的获利。
三角形面积= 3/16 ≈ 0.19
0.5 + 0.19 = 0.69 < 0.7
使用经济学的算法租用设备的盈利仍然小于设备租用的投资。不应当租用该设备。
(3)博弈论的答案 Game Theory
经济学答案的局限在于仅仅考虑了自身产量的变化。

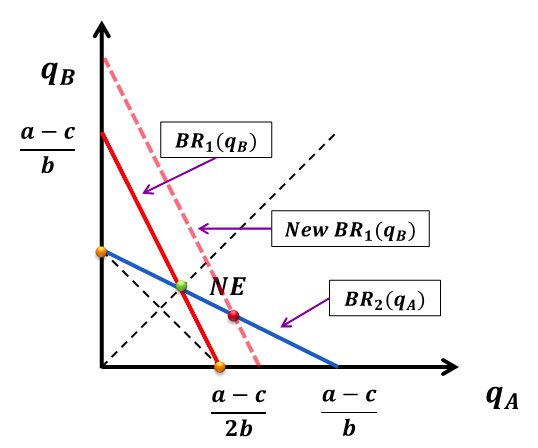
战略替代 (Strategic Substitutes)
因为 A 公司更新了设备,降低了成本,所以它的最优产量将会产生变化,形成一条新的最优反应虚线,即红色虚线。考虑到 A 公司的产量,B 公司会根据最优反应曲线来调整自己的产量,最终达成新的均衡,即由淡绿色点转变到红色点。
最终结果投资可以带来 31 万的利润,自行验证。
0.69 + 0.31 = 1 > 0.7
应当租用设备。
①先分析子博弈,找到子博弈的纳什均衡,从子博弈的价值出发回头做决定。
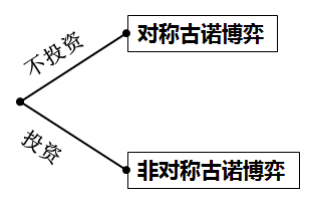
首先解出对称古诺竞争数据,解出新的均衡,回过头来和那要投资的 70 万作比较。 ② 经济学比会计学多考虑了战略效应(strategic effect),但却忽视了其他参与人也会改变行为。
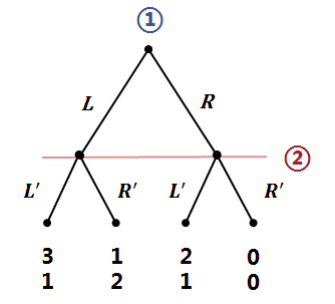
这里必须插入一个问题:关于博弈结果、博弈的均衡与博弈的均衡解博弈的结果等同于博弈的均衡解,但博弈的均衡跟均衡解不同,这里借用一个图说
明,在下图的两阶段博弈中,博弈的均衡解是(R,L'),但博弈的均衡却是(R,(R',L'))因为 NE 均衡是定义在 players 的策略之上,因此博弈的均衡策略要包含完整的计划这一点很重要,Ben 一直讲均衡解,但好像没怎么强调这个不同。
第二十讲 子博弈精炼均衡:消耗战
Subgame perfect equilibrium: wars of attrition
决斗博弈
两个参与人,每个阶段每个参与人可以选择攻击(Fight)或者退出(Quit),同时给出选择,直到一方退出后立即结束。
如果对手退出,我方得到奖励 = 1$ 如果双方都选择攻击,那么每人付出代价 − = −0.75$ 如果双方都选择退出,那么每人获得 0
消耗战(war of attrition)行贿竞赛(bribery contests)全薪拍卖(all pay auction)
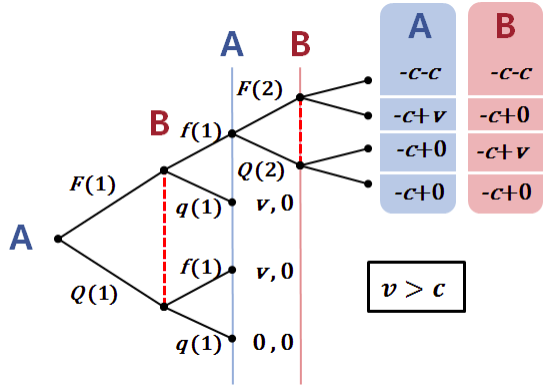
第二轮 B 的选择分支上为 f(2),下为 q(2),空间太小,省略了。
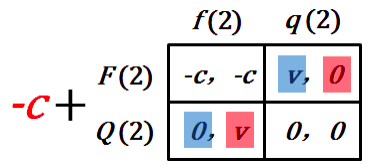
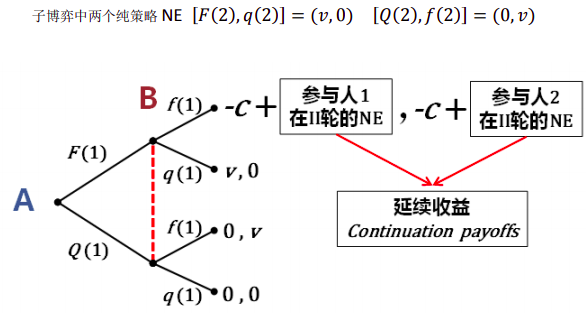
延续收益的两个均衡

两个纯策略博弈的完美均衡

求得均匀,却没有完成证明理智的参与者会选择在第一轮攻击如何去寻找一个折损较多的均衡?混合策略下的均衡
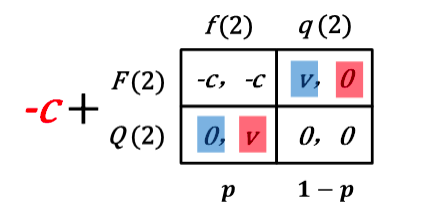

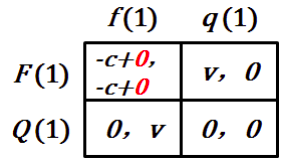
延续收益都为 0,即为第二阶段混合策略下的 NE 与子博弈的矩阵完全相同
混合策略下 SPE [(p∗, p∗)( p∗, p∗)]
收益期望为 0
将这个分析方式推广到无限博弈,分析结果也是一致的,在混合策略的 NE 下,延续收益仍然为 0
在消耗战为背景的博弈中,在理性参与人中有个一个均衡,更进一步说是一个合理的常识,即每个人都很理性,也知道其他人也是理性的,但却存在这样一个平衡,使人们不仅选择攻击而且一直攻击下去,在每个阶段他们有可能选择攻击。
随时间推移消耗战持续的可能性下降
第二十一讲 重复博弈:合作与最后一局游戏
Repeated games: cooperation vs. the end game
重复互动(Repeated Interaction)
在一个正在进行的关系中,对于将来奖励的承诺和未来惩罚的威胁,可能会为现在的好行为提供激励。

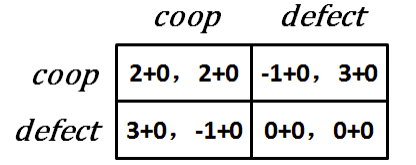
最后一轮都会背叛,因为没有一个将来的奖励,那么通过逆向归纳在这之前的一轮也会背叛,以此类推自始至终都会背叛。
前面类似例子垄断者威慑试图进入市场者的推演,见第十六讲。
要有一个明确的未来。
重复互动博弈的重点在于明确的未来会为现在的行动提供激励。
连任失败效应(lame duck effect)
两次博弈,收益矩阵如下
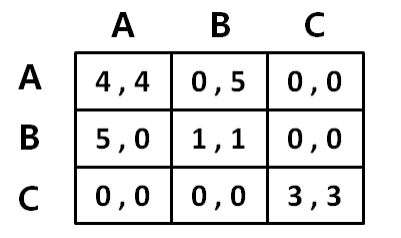
在一次性博弈中
(A,A)不是纯策略 NE
(B,B)(C,C)是纯策略 NE
在两次博弈中在第二阶段无法持续(A,A)
希望人们在第一阶段达成合作(A,A),考虑如下策略如果选了(A,A)就先选 A 再选 C,如果不是则选 B
从子博弈与第二阶段的联系开始
在(A,A)之后的第二阶段,有一个特别的子集,这个策略会促使(C,C)的发生。第一个阶段的其他选项之后会,会引发(B,B )
A → (A , A) = 4 + ( C, C) = 3 = 7
B → ( B,A ) = 5 + ( B, B) = 1 = 6
第一阶段背叛 ≤ 小于得到奖励的收益减去惩罚的收益背叛的收益在当前,奖励和惩罚在下一阶段,即
(B ,A ) − (A ,A ) ≤ ( B,B ) − (C ,C ) → 5 − 4 ≤ 3 − 1
结论:如果一个重复的阶段博弈,有不止一个 NE,可以通过预测不同策略造成的结果来未下一次行动提供激励,激励可视为奖励或者惩罚。
存在的问题,在第二阶段仍然有动机促使达成收益更高的均衡。
破产(Bankruptcy)担保(Bail Out)
事前和事后的权衡效率讨论 (discussion of trading off ex-ante efficiency and ex-post efficiency)
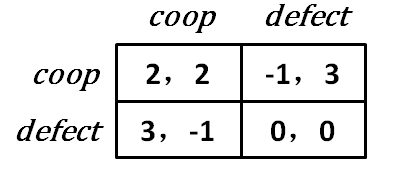
抛硬币决定何时结束博弈,双正面结束——75%的机会继续。
选 C 合作,如果之前没有选 D 就一直选 C,如果有人选 D 了,就一直选 D。
恐怖和扳机策略(Grim Trigger Strategy)
比较官方的叫法是触发战略,也有译法叫做冷酷战略的
与前面课程博弈的显著不同——无法确定博弈何时结束,没有明确的最后阶段,那么参与人便无法确定在什么时候背叛来赢得最后阶段的更高收益。
检查这种持续合作是否是一个均衡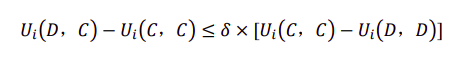
今天背叛的收益与保持合作的收益差异 ≤ 下一轮保持合作收益与保持背叛收益差额与博弈继续下去概率的乘积
第二十二讲 重复博弈:作弊,惩罚和外包
Repeated games: cheating, punishment, and outsourcing
听这讲时用的圣城的字幕,其他都是 YYeTs 人人影视的字幕,鉴于对前者风格不太熟悉的原因,本讲笔记可能更繁琐一些,为了避免漏掉有用的成分,有重复的部分各位见谅。
权衡良好行为带来的前景,和不良行为招致的损失,从而抑制我们作弊的念头。现在作弊的利益 ≤ 今后合作的利益(承诺 promise) − 今后欺骗的代价(threat)
需要承诺和威胁都真实可信
今天的威胁不可信,因为明天仍然会遵循 NE,那么今天的合作就没了基础保持威胁真实可信的方法是关注 SPE——特点每一个子博弈中都有 NE,利用这个特点来寻找合作机会
这个问题具有重复性,称为 ,每个时期,的可能性在延续,如果可能性是1 − 那么可能博弈每个时期都会结束。

现在作弊的利益 ≤ 今后合作的利益 − 今后欺骗的代价
3 − 2 ≤ 永远合作(C ,C) = 2 −永远背叛(D ,D) = 0
永远合作的收益:
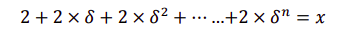
解得:
假设博弈可以进行下去的概率为 p,贴现因子为 1/(1+r),下期可以得到的收益是π,那么如果可以进行到下期那么本期的收益为 pπ/(1+r),再下一期同样分析,那么如果设 P/(1+r)=delta 作为新的贴现因子,那么这个因子就既包括了时间价值又包括了博弈能够继续进行的可能性了,不是不恰当的。
求证恐怖和扳机策略能实现:
 ⇔
⇔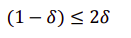 ⇔
⇔ 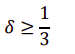
当满足这个条件时不会选择背叛
验证是否存在有利的策略变更:
先选 D,之后在下一时段选 C,之后永远选 D,结果会如何?


重复道德风险 (Repeated Moral Hazard)
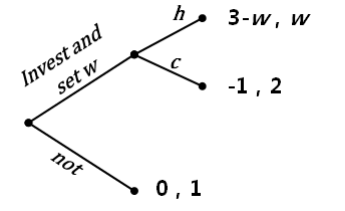
在 Freedonia 不投资,那么收益为 0,代理人只获得基本工资 1(从事其他工作);如果投资,并设定工资为 W,此时代理人,可以选择诚实(Honest)或背叛(Cheat)。如果参与人选择背叛,那么投资损失原材料,代理人获得卖出原材料的收益 1,以及从事其他工作的获得的基本工资 1。
如果代理人选择诚实,那么我方的利润是 4,减去支付给代理人的基本工资 1,投资人的收益为3 − w,代理人的收益为w
假设这是一次性投资,为了生产顺利完成,我要付给代理人多少工资?
运用 BI,若w = 1,那么代理人会选择背叛需要做的是让工资足够高,使得代理人诚实并继续项目,并被判获得的多,需要w ≥ 2
w∗ = 2
如果你担心雇员会有背叛的动机,为了让他们工作,你需要支付巨大的工资溢价, Freedonia 的基本工资是 1,但你需要设定工资等于 2,一个 100%的工资溢价,以让其工作.
重复互动,持续下去的概率为𝛿
在此情况下要付的工资 w∗∗
今天背叛的诱惑 ≤ [ 继续关系值(继续雇佣) − 终止关系值(解雇) ]
The value of continuing the relationship minus the value of ending the relationship
即是关系继续下去的概率相对较小,也会大幅度减少工资溢价
为了在这些持续关系中获得良好行为,必须要在明天提供一定的报酬如果你放到明天的砝码,或者说,如果明天继续下去的概率比较低,那么这个报酬就要比较高
第二十三讲 非对称信息:沉默,信号和教育之苦
Asymmetric information: silence, signaling and suffering education
第一部分 信息能够被证实的情况
古诺模型,两家企业 A 和 B,假设 B 的边际成本 位于高低之间企业 A 的成本有三种情况: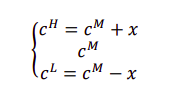
企业 B 只知道自己的成本,而企业 A 知道双方的成本,企业 A 可以选择是否告诉企业 B 自己的成,令企业 B 相信企业 A 的成本无需额外的花销。
关于策略替代,租用设备降低成本,见第十九讲后半节的讨论,会计学、经济学、博弈论
应该是一开始讲古诺模型的时候
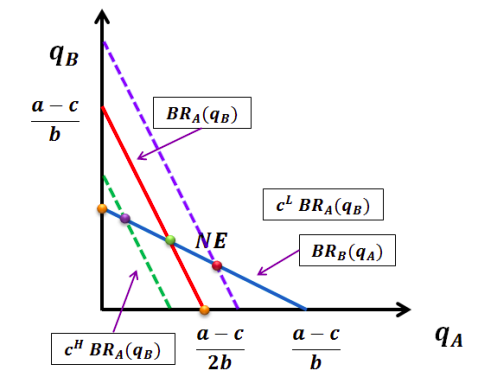

既然三种情况的两种的需要曝光,那么剩下也没什么好隐瞒的了。
信息披露的过程 (Informational Unraveling)
重要结论:缺乏信息传达途径,或者说企业不像公布一些信息,这些现象本身也在传达着信息。
传递信号有成本的模型 (Costly Signaling)
优秀雇员 good workers——G——绩效 50——10% 差劲雇员 bad workers——B——绩效 30——90%
企业支付给优秀员工薪水——50;差劲雇员——30对于无法评价的一般员工支付 32(B G 加权平均)
马克·斯彭斯 Mike Spence
成本差异化,假设获得 MBA 学位每一年的成本对于优秀的雇员来说是 5,而对于差劲的雇员来说是 10。学费等价,且假设不存在机会成本,成本的差异体现在付出的精力。
有 MBA 就是好雇员,否则就是差雇员
证明均衡:
① 证明每一类雇员都不愿意改变
② 证明雇主的想法和均衡行为是一致的
假设每个雇员都只工作一年
G-worker → MBA → 雇主认为该员工是好雇员 → 收益 绩效工资 50−扣除成本 3 × 5(三年,每年 5)总收益为 35 ·作出改变 → 没有 MBA → 雇主认为该员工是差雇员 → 收益 绩效工资30 < 35
B-worker → 没有 MBA → 雇主认为该员工是差雇员 → 收益 绩效工资 30 ·作出改变 → MBA → 雇主认为该员工是好雇员 → 收益 绩效工资50 − 扣除成本
3 × 10(三年,每年 10)总收益为 20< 30
此案例为分离均衡(separating equilibrium)
貌似 Ben 没有时间讲混同均衡
假设取得 MBA 只需要 1 年,带入上面的分析 B-worker 取得 MBA 收益变为 40 优于没
有 MBA 的 30
判断优秀员工与差劲员工需要取得 MBA 时间至少为 2 年
在成本上有足够的差别,是优秀的员工去念 MBA,而差劲的员工不想这么做。
结论:
一个好的信号不一定与很高的成本有关,但是要能通过成本区别不同的类型。
此处模型的缺陷:
(1)模型中没有学习的概念(2)教育失去了社会用途,仅仅成为了区别优秀与差劲的工具(3)教育加剧了不平等
第二十四讲 非对称信息:拍卖和获奖者的诅咒
Asymmetric information: auctions and the winner's curse
拍卖(Auction)
公共价值(common values)
私人价值(private values)
被出售商品的价值用[ V ]标记公共价值
私人价值,物品的最终价值对每个人都不同,它完全具有特异性,并且我对它赋予的价值和你是没有关系的 [ ]
油井 住房 蛋糕
拍卖——罐子中硬币
最后胜出的出价要比实际价值高许多
赢家的诅咒(winner's curse)
拍卖中的收益情况
V——罐子中的硬币数-参与人的竞价(最高的出价)
0
人们的估价值
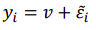
可以它当作真实价值,加偏差值
正态分布图像
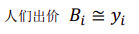
获胜者是出价最大值 的参与人 i , 意味着偏差值最大
一般来说最后获胜的出价会比真实价值高很多
首次公开募股(Initial Public Offerings,简称 IPO)
油井的例子
每个公司都在油田里挖一个测试井,从测试井中每个公司都得到一个估值
假设参与人 i 的估值等于yi = 150,当被告知 𝑦j < 𝑦i ,对所有 j 都成立
当参与人赢得拍卖时他会发现这个问题,而这会引起参与人的后悔
如果参与人 i 只考虑油井里有多少油,且赢得了拍卖,因此参与人做出的估值 至
少要和其他所有人的估值yj 一样大,即yi ≥ yj
所以出价时的相关价值就是,基于参与人 i 一开始的估价以及这个估价值yi 要比yj大时,
应该出假设参与人 i 自己是最后的赢家,参与人 i 估计出来的罐子中的硬币数,应该像赢家那样去出价
拍卖形式
A首价密封拍卖机制 First-price Sealed-bid auction A=D
B第二价格密封拍卖 Second-price Sealed-bid auction 赢家支付第二高的出价维克瑞拍卖 (Vickrey auction)
C公开增价拍卖 (Ascending open auction)
D 公开降价拍卖 (Descending open auction) 逐步降价直到有人提出购买荷兰式拍卖 (Dutch auction)D=A
B 和 C 不同但密切相关
B≈C,区别不在价格上而是在信号上
私人价值的拍卖 参与人出价 𝐵𝑖 收益:



