一、基础知识
-
PyTorch提供简单的计算误差方法。最简单的均方误差：先计算每个输出节点的实际输出和预期输出之差的平方，再计算平均值。
nn.MSELoss() -
误差函数&&损失函数
- 误差是指预期输出与实际输出之间的差值。
- 损失是指根据误差计算得到的，要考虑实际情况。
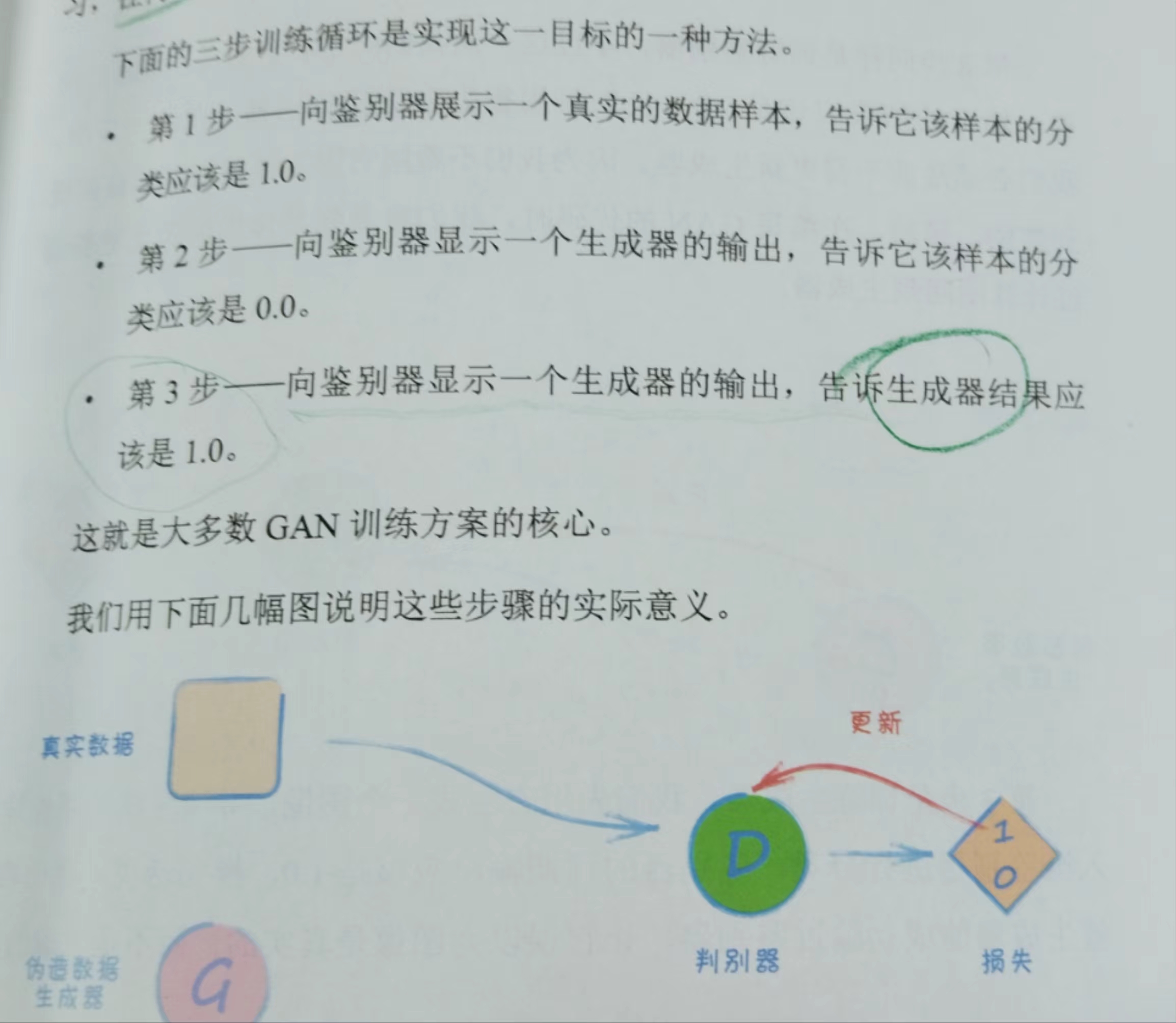
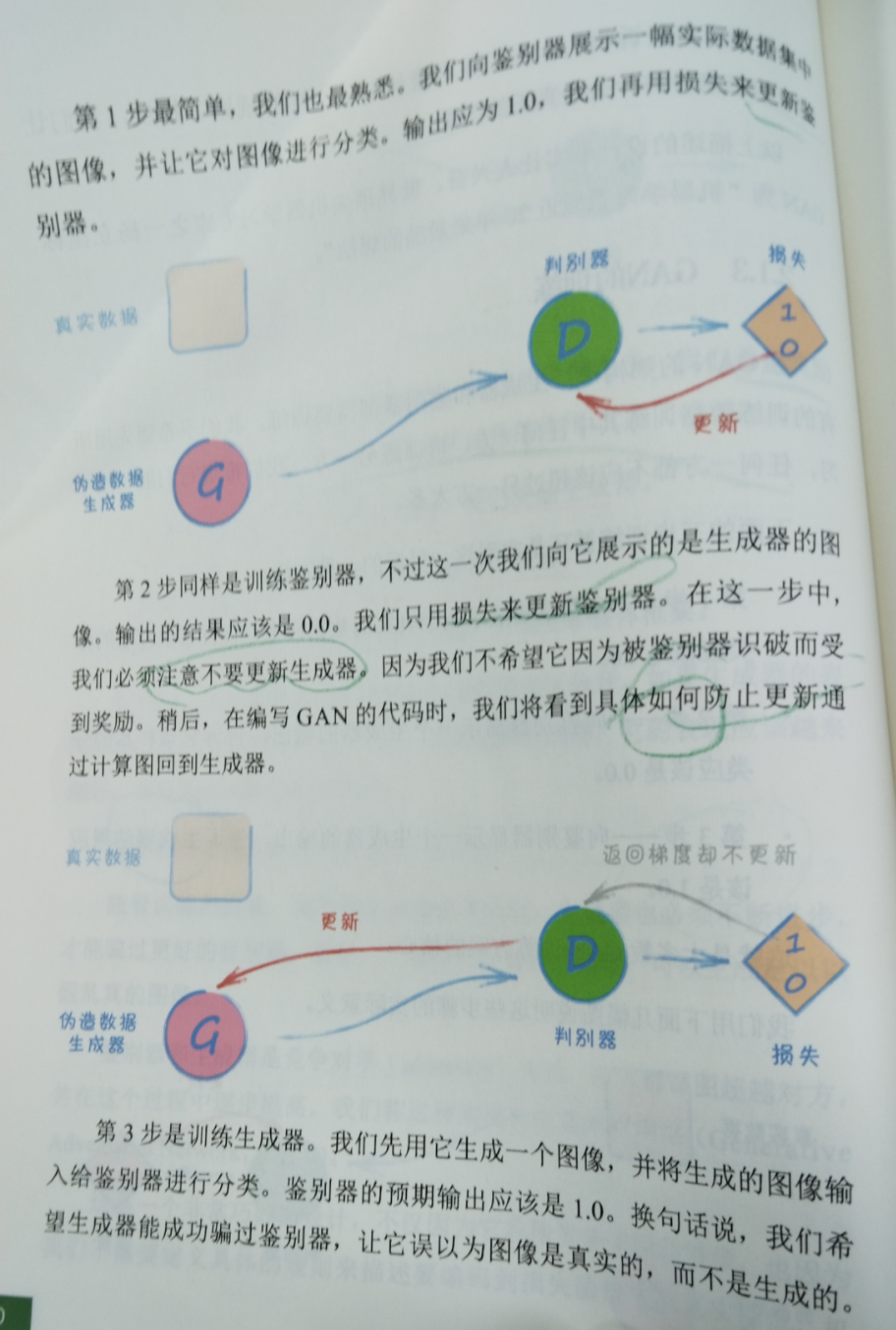
1、构建和训练GAN的推荐步骤：
- 从真实数据集预览总数据
- 测试鉴别器至少具备从随机噪声中区分真实数据的能力
- 测试未经训练的生成器能否创建正确格式的数据
- 可视化观察损失值，了解训练进展
-
理想的损失值应该在0.25左右，也就是鉴别器和生成器达到平衡。如果鉴别器的损失值趋近于0，表明该生成器没能学会骗过鉴别器
-
在鉴别器学会向生成器提供良好的反馈之前，生成器率先发现一个一直被判定为真实图像的输出
-
如何解决模式崩溃和图像清晰度低的问题。
1）使用二元交叉熵BCELoss()代替损失函数中的均方误差MSELoss（）
2）在鉴别器和生成器中使用LeakyReLU（）激活函数。
3）将神经网络中的信号进行标准化，确保它的均值为0.改良后的神经网络的代码如下：
self.model=nn.Sequential( nn.Linear(784,200), nn.LeakyReLU(0.02), nn.LayerNorm(200), nn.Linear(200,1), nn.Sigmoid()
4)使用Adam优化器
上述改良方法并没有改变末世崩溃现象，但是解决了图像清晰度问题。 -
生成器会觉得，讲一个单值转换成784像素来代表一个数字太难了。试着将输入值从1变成100，仍然没有解决模式崩溃问题。
-
输入鉴别器的随机种子和生成器的随机种子可以不一样。因为输入生成器的种子不需要01范围内。而输入鉴别器的种子需要在01范围内，才可以对应真实数据集中的图像像素问题。
-
怎么样选取一个合适的随机种子？
要从一个平均值为0，方差为1的正态分布中抽取种子更加合理。 -
所以最后的改良方法是将鉴别器和生成器的随机种子分别设置不同的范围，并加上之前的所有改良方法，是所有的组合效果。
-
最优BCE损失的理想损失值为ln2或0.693。
11.种子相加也会造成它们生成的图像的叠加。可以试一下种子实验。
-
模式崩溃就是指一个生成器在有多个可能输出类别的情况下，一直生成单一类别的输出。
-
分层数据格式：就是一个组里包含多个数据集，甚至多个组。
-
将这种在图像上移动并汇总新的网格的过程称为卷积。
卷积核将识别低层次特征，并将这些信息汇总在网格中。这些网格的正式名称是特征图。如果将另一层卷积核应用到这些特征图上，我们可以得到中层次的特征。这些特征是低层次的组合。 -
基本上，我们只需要决定使用几个卷积核，比如20个，在训练过程中，我们会对没个卷积核内部的权重进行调整。如果训练成功，最终得到的卷积核会从图像中挑出最有代表性的细节。
16.代码查看当前所分配的内存大小
torch.cuda.memory_allocated(device)/(1024*1024*1024)
代码查看内存消耗
print(torch.cuda.memory_summary(device,abbreviated=True))
-
机器学习的黄金法则是，最大限度地利用与当前问题相关的知识。这些领域知识可以帮助我们排除不成立的选项，从而简化问题空间。
-
应该构建最小的网络，这样训练起来比较容易，但不能小到失去学习能力。
-
遵循一个原则：生成器应该是鉴别器的镜像
-
卷积的反义词：转置卷积。需要调用的模块是nn.ConvTranspose2d
-
鉴别器的过程：
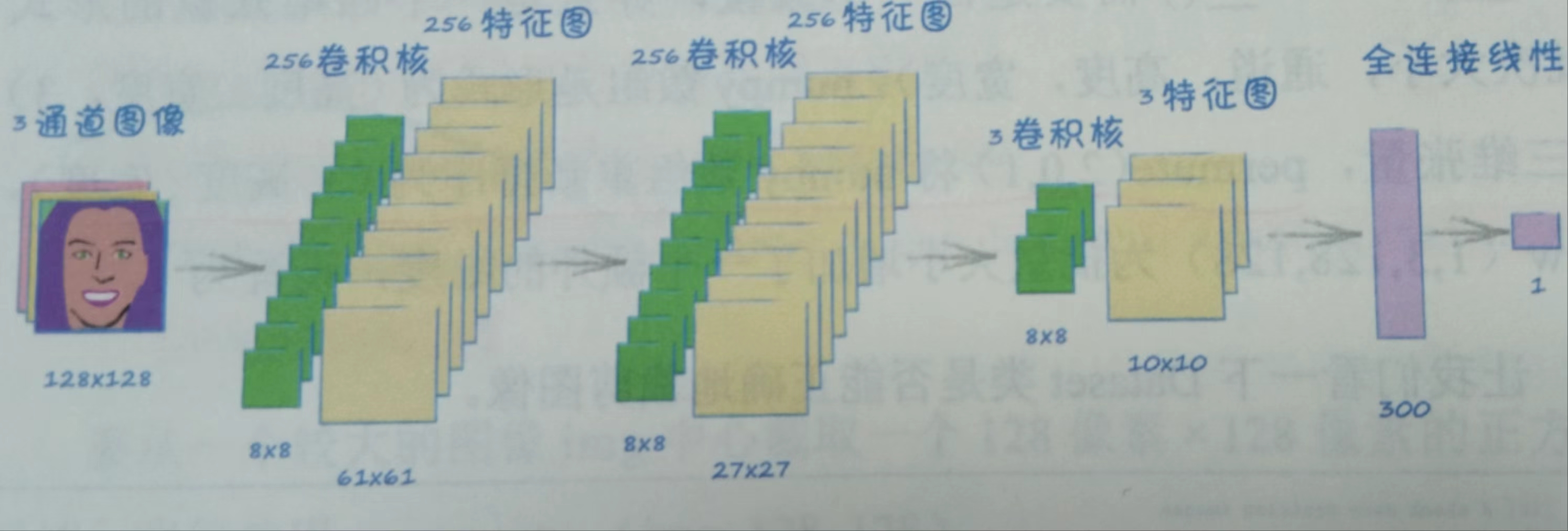
生成器的过程：
-
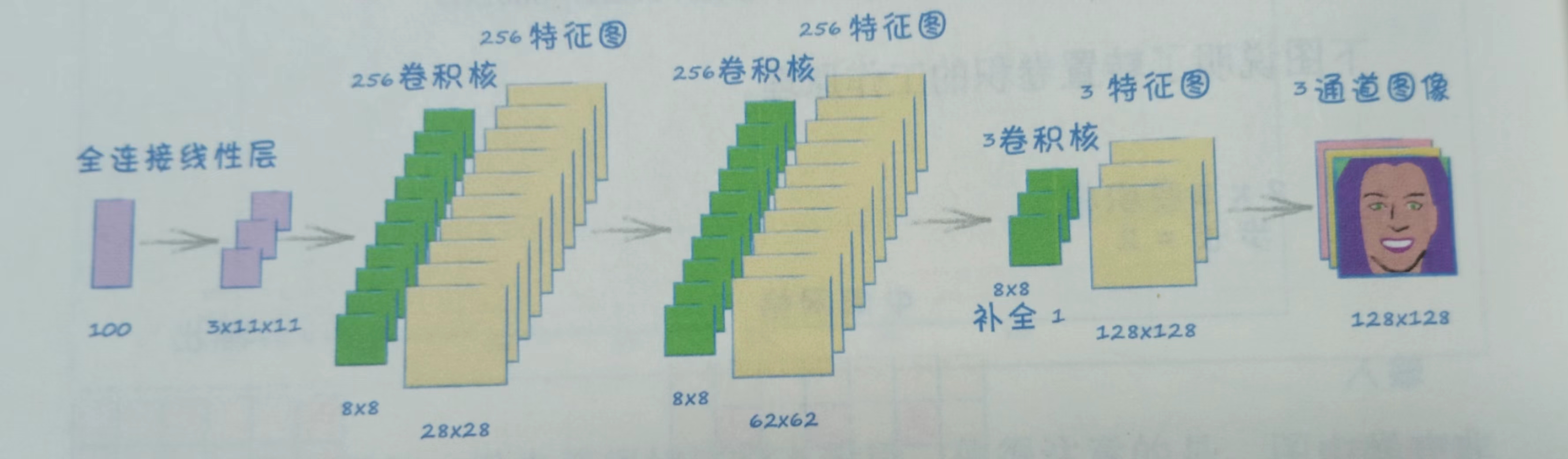
卷积网络中每一个特征的生成，都是在缺乏上层图像的完整视角的情况下进行的。
-
卷积生成器的一个缺点是，他可能生成由相互不匹配的元素组成的图像，这是因为卷积网络处理的信息是局部化的，而全局关系并没有被学习到。（很重要！！！！）
-
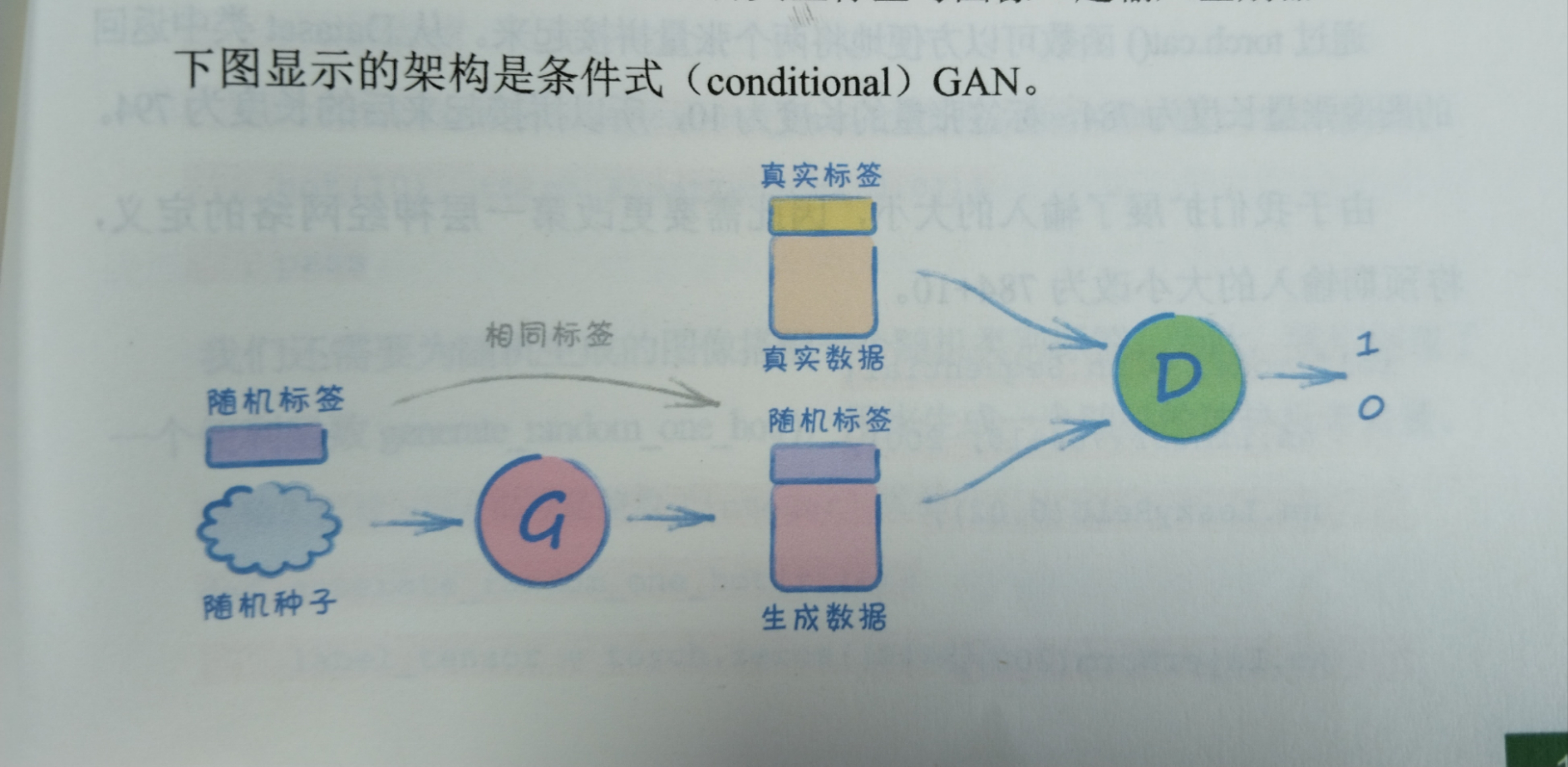
条件式GAN架构
1）将类型作为生成器输入的一部分，如同随机种子一样。
2）鉴别器的工作到了条件式架构上，就不只是将真实的图像与生成的图像分开，而且还要学习将类型标签与图像关联起来。不然它就无法向生成器提供反馈，生成器也就无法将图像与标签关联起来。这就意味着，我们需要将类型标签域图像一起输入鉴别器。
-
在训练GAN时，希望达到的理想状态是，生成器与鉴别器之间达到平衡，可以通过均方误差损失、二元交叉熵损失，来计算在平衡时鉴别器的损失值应该是多少。
1）均方误差：如果鉴别器输出为0.1，而目标值为1，则误差为0.5；当目标为0时，误差为-0.5.这两个误差经过平方后，结果都会得到0.25.
2）熵是描述不确定性的数学概念。（一个例子解释熵：假设有一枚不公平的硬币，两面都是正，那么得到的正面的概率就是100%，同样，得到反面的概率就是0%，在任意一种情况下，我们对结果都是100%确定的。由于不确定性是0，因此我们就说熵是0。现在这枚硬币是公平的，此时我们对结果的不确定最大，即熵最大）
3）交叉熵：同样是衡量结果的不确定性，这种不确定性，是由结果的实际可能性与我们预想的可能性之间的差异而导致的。（理解为：以上个式子为例，如果我们认为这个硬币是公平的，但其实是不公平的，我们就会感到意外。这些结果也就具有了不确定性，这就是交叉熵要衡量的信息）可以把交叉熵看成两个概率之间的分布。他们相似度越高，交叉熵就越小，两个概率分布完全相同时的交叉熵为0.
交叉熵和神经网络之间的联系：神经网络的目标输出是概率分布，而实际输出也是概率分布，如果他们之间的差异很大，交叉熵也就很大。置信度高却错误的输出也有较大的交叉熵。对分类任务更适合使用交叉熵。关键原因在于它对错误输出的惩罚力度更大。交叉熵与MSE损失的区别在于它包含对数，造成它的取值范围比1.0大得多。这种陡峭的损失函数可以反馈给神经网络很大的梯度。
