图论 —— 生成树 —— 最小树形图
【概述】
最小树形图,就是给出一个带权有向图,从中指定一个特殊的结点 root,求一棵以 root 为根的有向生成树 T,且使得 T 中所有边权值最小。
简单来说,最小树形图就是有向图的最小生成树。
【朱刘算法】
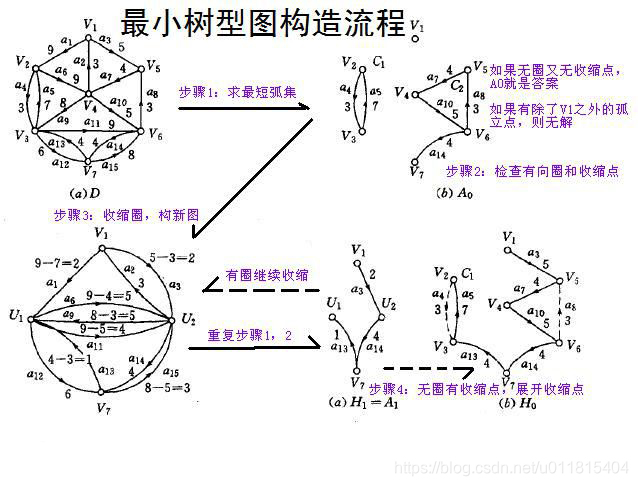
1.过程
简单来说,朱刘算法分为四个过程:
1)求最短弧集合 E
2)判断集合 E 中有没有有向环,如果有转步骤 3,否则转 4
3)收缩点,把有向环收缩成一个点,并且对图重新构建,包括边权值的改变和点的处理,之后再转步骤 1
4)展开收缩点,求得最小树形图
2.实现
struct Edge{
int x,y;
int w;
}edge[N];
int vis[N];
int id[N];//结点所属环编号
int in[N],pre[N];//in[]为最小入边权,pre[]为其对应的起点
int zhuLiu(int root,int n,int m){//root结点、点数、边数
int res=0;//最小树形图总权值
while(true){
for(int i=0;i<n;i++)//初始化为无穷大
in[i]=INF;
//寻找每个点的最小入边
for(int i=0;i<m;i++){//遍历每条边
int x=edge[i].x;
int y=edge[i].y;
if(edge[i].w<in[y] && x!=y){//更新最小入边
pre[y]=x;//记录前驱
in[y]=edge[i].w;//更新
}
}
//判断是否存在最小树形图
for(int i=0;i<n;i++){
if(i==root)
continue;
if(in[i]==INF)//除根节点外的点存在孤立点
return -1;
}
//寻找所有的环
int cnt=0;//记录环数
in[root]=0;
memset(id,-1,sizeof(id));
memset(vis,-1,sizeof(vis));
for(int i=0;i<n;i++){//标记每个环
res+=in[i];//记录权值
int y=i;
while(vis[y]!=i&&id[y]==-1&&y!=root){//寻找图中有向环
//三种情况会终止:找到出现同样标记的点、结点已属其他环、遍历到根
vis[y]=i;//标记
y=pre[y];//向上找
}
if(y!=root&&id[y]==-1){//没有遍历到根或没有找到结点属于其他环,说明找到有向环
for(int x=pre[y];x!=y;x=pre[x])//标记结点x为第几个环
id[x]=cnt;//记录结点所属环号
id[y]=cnt++;//记录结点所属环号并累加
}
}
if(cnt==0)//无环
break;
for(int i=0;i<n;i++)//可能存在独立点
if(id[i]==-1)//环数累加
id[i]=cnt++;
//建立新图,缩点重新标记
for(int i=0;i<m;i++){
int x=edge[i].x;
int y=edge[i].y;
edge[i].x=id[x];
edge[i].y=id[y];
if(id[x]!=id[y])//两点不在同一环内,更新边权值
edge[i].w-=in[y];//x到y的距离为边权-in[y]
}
n=cnt;//以环数为下次操作的点数,继续上述操作,直到无环
root=id[root];
}
return res;
}
int main(){
int n,m;//n个点m条有向边
scanf("%d%d",&n,&m);
for(int i=0;i<m;i++){//建图
scanf("%d%d%d",&edge[i].x,&edge[i].y,&edge[i].w);
if(edge[i].x==edge[i].y)//除去自环,即点到自身距离为INF
edge[i].w=INF;
}
int res=zhuLiu(0,n,m);
if(res==-1)
printf("No\n");
else
printf("%d\n",res);
return 0;
}




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· NetPad:一个.NET开源、跨平台的C#编辑器
· PowerShell开发游戏 · 打蜜蜂
· 凌晨三点救火实录:Java内存泄漏的七个神坑,你至少踩过三个!