transformer之我观

transformer模型学习有感

一个 transformer 模型用自注意力层而非 Rnn 或 Cnn 来处理变长的输入。这种通用架构有一系列的优势：

它不对数据间的时间/空间关系做任何假设。这是处理一组对象（objects）的理想选择。
层输出可以并行计算，而非像 RNN 这样的一步一步的计算。
远距离的两个项可以影响彼此的输出，而无需经过许多 RNN 步骤或卷积层。
它能学习长距离的依赖关系。在Rnn和Cnn中会产生梯度消失，难以更新神经网络浅层的参数。

该架构的缺点是：

对于时间序列，一个单位时间的输出是从整个历史记录计算的，而非仅从输入和当前的隐含状态计算得到。这可能效率较低。
如果输入确实有序列的关系，比如文本，则必须加入一些位置编码，否则模型只会看到一堆单词而不是一个有序列关系的句子。

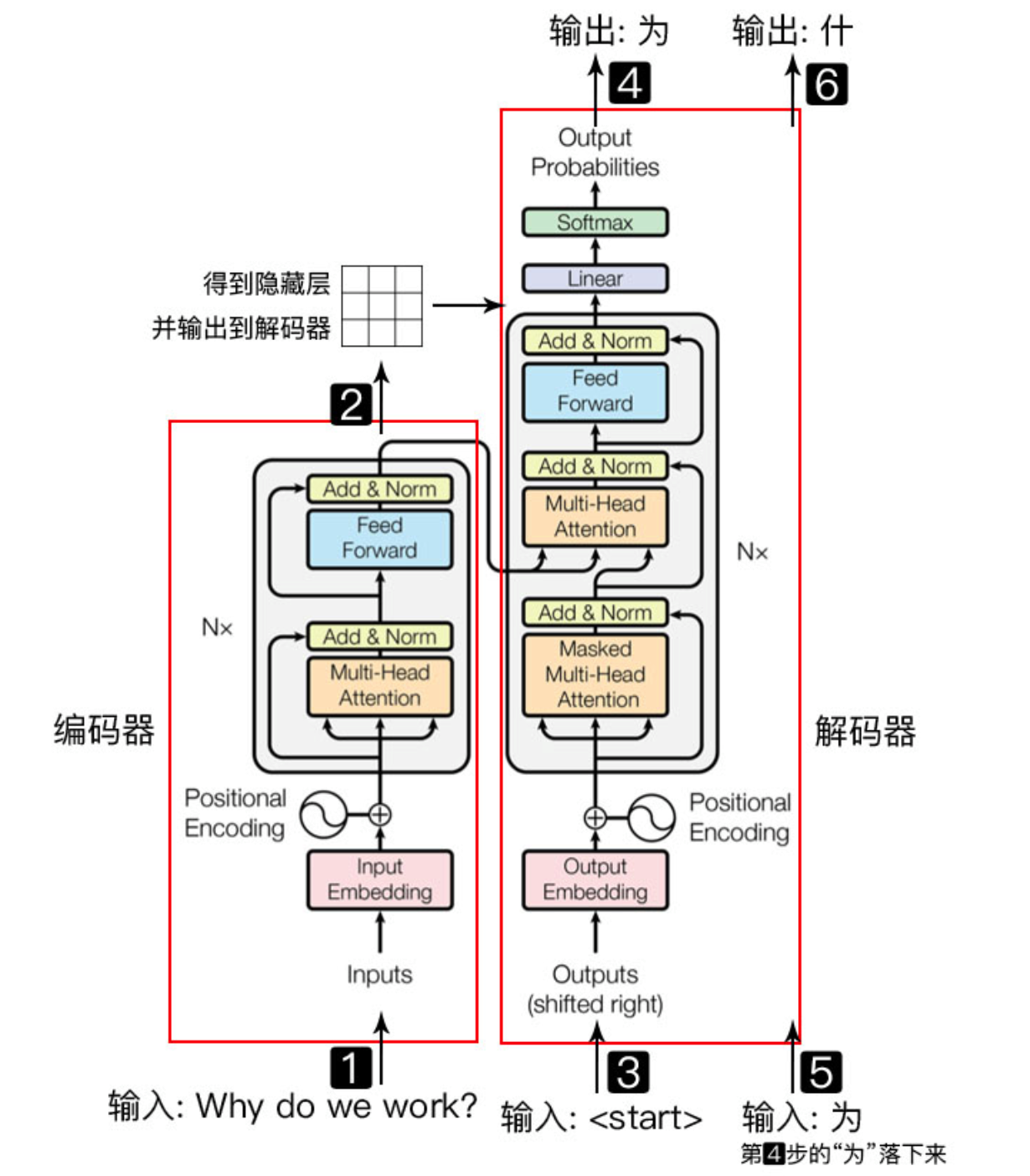
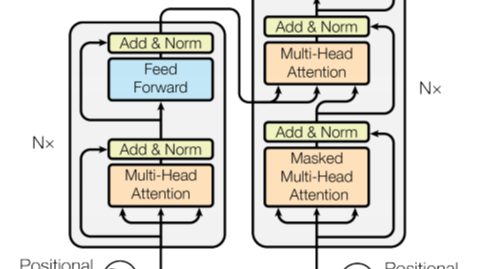
首先是transformer最经典的architecture架构图。

其中，Encoder负责将输入\((x_1, x_2, ..., x_n)\) 转换为 \((z_1,z_2,...,z_n)\) 的输出，其中 \(x_t\) 是我们原始输入的第t个词，\(z_t\) 是这个词的向量表示。在每个时刻 \(t\) Decoder拿到Encoder的输出 \((z1,...,zn)\) ，通过自回归来生成预测序列 \((y_1, y_2, ...,y_m)\)，也就是将过去时刻的输出作为我第t时刻的额外输入。（即步骤3）

Encoder架构

主要分为五个部分，下面将以原论文中的顺序依次讲解。

1. Inputs Embedding

就是我们在处理文本类输入时常用的词嵌入word2vec，用来将一个字表示成一个向量。

不同于One-Hot编码的“没有任何的相对关系，只是一串01向量”；embedding可以看作是将每个单词的One-Hot编码向量乘以一个参数矩阵 \(W_0\)，输出就是这个单词的词向量但是输出的embedding向量的维度一般小于One-Hot编码。

transformer将所有词向量的embedding都设置为512

2. Positional Encoding

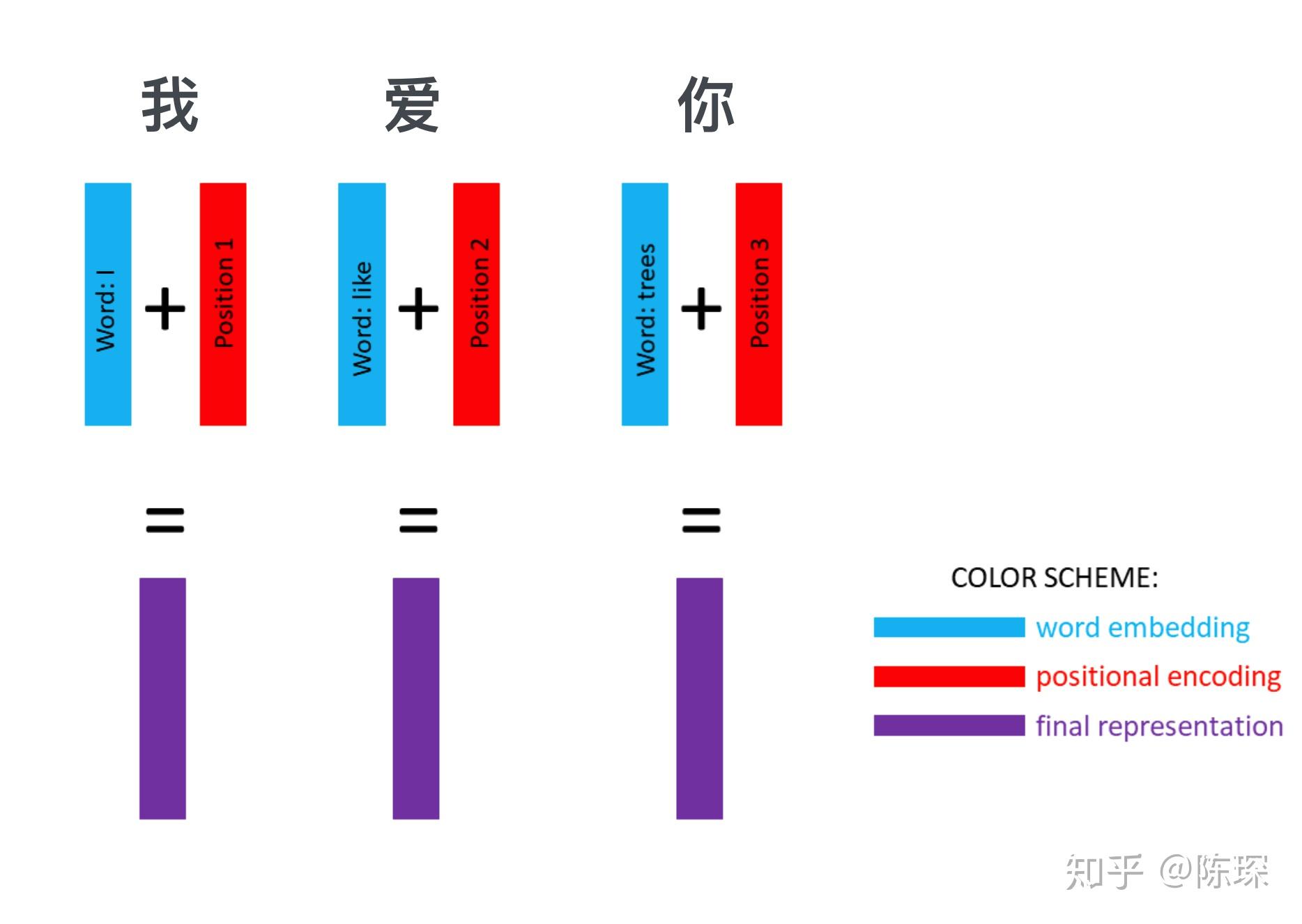
因为transformer中没有任何的rnn或者cnn，完全依赖于注意力机制来建立输入和输出之间的关系。但是我们的输入是一个句子，会包含序列信息。不同于RNN会按顺序处理每一个字，天然的有序列关系，transformer需要对输入添加位置编码。也就是对输入序列中的每一个字 \(x_i\) ，我们都在其中添加一个关于 \(i\) 的相对位置编码。

def positional_encoding(position, d_model):
  ---算角度
  angle_rads = get_angles(np.arange(position)[:, np.newaxis],
                          np.arange(d_model)[np.newaxis, :],
                          d_model)

  # 将 sin 应用于数组中的偶数索引（indices）；2i
  angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])

  # 将 cos 应用于数组中的奇数索引；2i+1
  angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])
  pos_encoding = angle_rads[np.newaxis, ...]
  ---
  return tf.cast(pos_encoding, dtype=tf.float32)#将位置信息转换为float

pos_encoding = positional_encoding(50, 512)
print (pos_encoding.shape)

>>>(1, 50, 512)

Input Tensor 的 size 为 [batch_size, seq_length, 512]：

batch_size 指的是定义的批量大小 batch_size
seq_length 指的是 sequence 的长度，(比如“我爱你”，seq_length = 3)
512 指的是 embedding 的 dimension

3.多头+自注意力机制

3.1 Scaled Dot-Product Attention

注意力函数就是通过矩阵乘法，求得query矩阵和key矩阵的向量乘法，得到注意力矩阵。经过一层softmax之后，再跟value矩阵相乘。

注意力矩阵的第i行的含义是：第i个q跟所有的k的相似度，可以理解为向量做内积。所以我们对每行做softmax之后，就会得到对于这个query向量对于所有key向量的相似度，并且相加为1。

def scaled_dot_product_attention(q, k, v, mask):
  """计算注意力权重。
  q, k, v 必须具有匹配的第一个维度，也就是batch_size样本容量
  k, v 必须有匹配的倒数第二个维度，也就是seq_len_k = seq_len_v，因为key矩阵和value矩阵一定有相同的
  虽然 mask 根据其类型（填充或前瞻）有不同的形状，
  但是 mask 必须能进行广播转换以便求和。
  
  参数:
    q: 请求的形状 == (batch_size, seq_len_q, depth)
    k: 主键的形状 == (batch_size, seq_len_k, depth)
    v: 数值的形状 == (batch_size, seq_len_v, depth_v)
    mask: Float 张量，其形状能转换成
          (..., seq_len_q, seq_len_k)。默认为None。
    
  返回值:
    输出，注意力权重
  """

  matmul_qk = tf.matmul(q, k, transpose_b=True)  # (..., seq_len_q, seq_len_k)
  
  # 缩放 matmul_qk
  dk = tf.cast(tf.shape(k)[-1], tf.float32)
  scaled_attention_logits = matmul_qk / tf.math.sqrt(dk)

  # 将 mask 加入到缩放的张量上。
  if mask is not None:
    scaled_attention_logits += (mask * -1e9)  

  # softmax 在最后一个轴（seq_len_k）上归一化，因此分数（对注意力矩阵每一行归一化，则每个字的注意力向量一行，就是与其余字的相关程度）相加等于1。
  attention_weights = tf.nn.softmax(scaled_attention_logits, axis=-1)  # (..., seq_len_q, seq_len_k)  注意力矩阵

  output = tf.matmul(attention_weights, v)  # (..., seq_len_q, depth_v)  再把注意力矩阵乘V

  return output, attention_weights

3.2 多头注意力

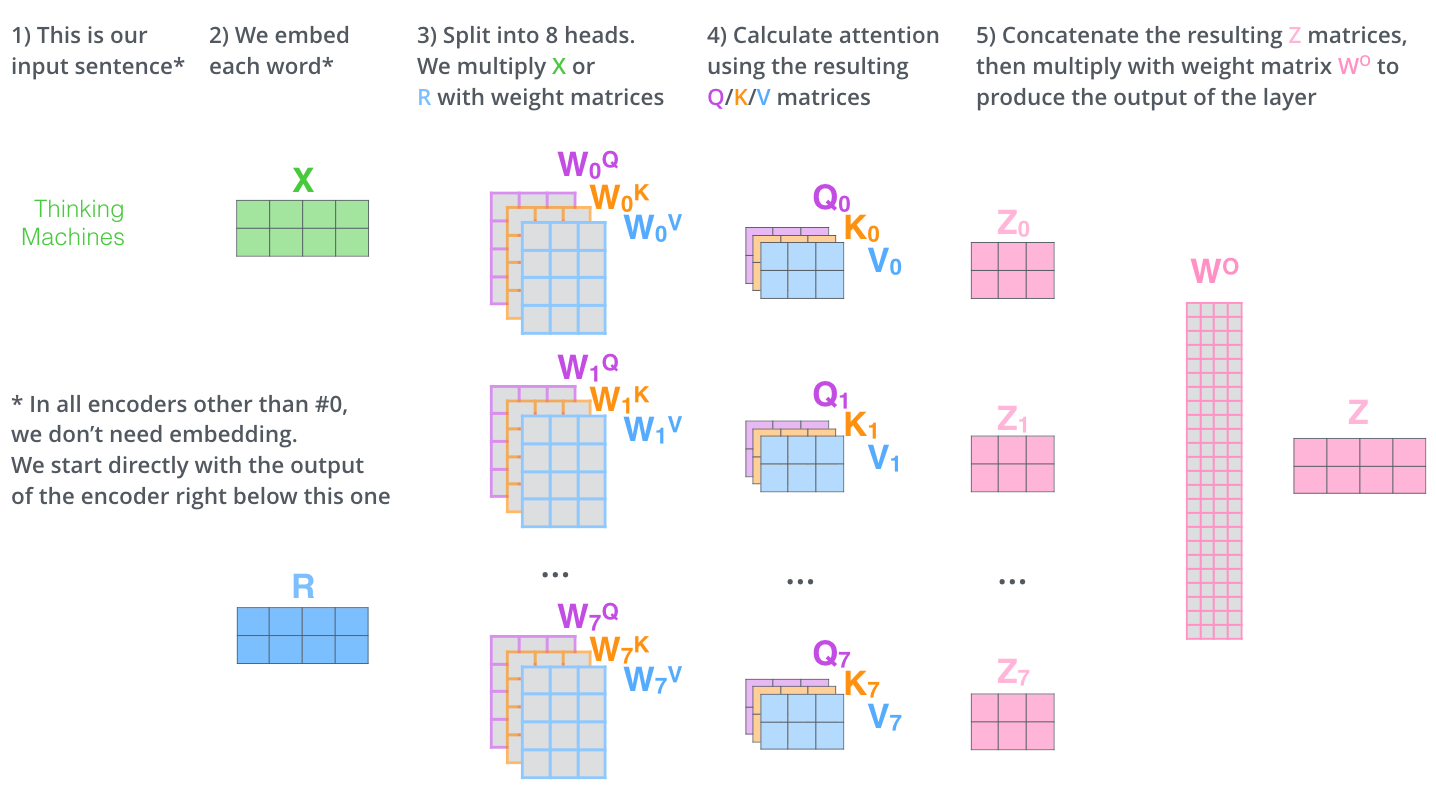
对于多头注意力机制，也就是我们与其做一次注意力机制，不如我们把 q，k，v 投影到一个低维的空间，其中每个头的输入维度中，embedding减少到之前的 \(1 / h\) ，再分别做h次注意力机制。将得到的h个结果并起来，并重新将结果映射回高维，就得到我们需要的注意力输出了。

可以类比CNN中的多卷积核的作用——每次抽取不同特征，得到多个不同的特征通道。

class MultiHeadAttention(tf.keras.layers.Layer):
  def __init__(self, d_model, num_heads):
    super(MultiHeadAttention, self).__init__()
    self.num_heads = num_heads
    self.d_model = d_model

    assert d_model % self.num_heads == 0

    self.depth = d_model // self.num_heads

    self.wq = tf.keras.layers.Dense(d_model)
    self.wk = tf.keras.layers.Dense(d_model)
    self.wv = tf.keras.layers.Dense(d_model)

    self.dense = tf.keras.layers.Dense(d_model)

  def split_heads(self, x, batch_size):
    """
    分拆最后一个维度到 (num_heads, depth).
    转置结果使得形状为 (batch_size, num_heads, seq_len, depth)
    """
    x = tf.reshape(x, (batch_size, -1, self.num_heads, self.depth))
    return tf.transpose(x, perm=[0, 2, 1, 3])

  def call(self, v, k, q, mask):
    batch_size = tf.shape(q)[0]

    q = self.wq(q)  # (batch_size, seq_len, d_model)
    k = self.wk(k)  # (batch_size, seq_len, d_model)
    v = self.wv(v)  # (batch_size, seq_len, d_model)

    q = self.split_heads(q, batch_size)  # (batch_size, num_heads, seq_len_q, depth)
    k = self.split_heads(k, batch_size)  # (batch_size, num_heads, seq_len_k, depth)
    v = self.split_heads(v, batch_size)  # (batch_size, num_heads, seq_len_v, depth)

    # scaled_attention.shape == (batch_size, num_heads, seq_len_q, depth)
    # attention_weights.shape == (batch_size, num_heads, seq_len_q, seq_len_k)
    scaled_attention, attention_weights = scaled_dot_product_attention(
        q, k, v, mask)

    scaled_attention = tf.transpose(scaled_attention, perm=[0, 2, 1, 3])  # (batch_size, seq_len_q, num_heads, depth)

    concat_attention = tf.reshape(scaled_attention, 
                                  (batch_size, -1, self.d_model))  # (batch_size, seq_len_q, d_model)

    output = self.dense(concat_attention)  # (batch_size, seq_len_q, d_model)

    return output, attention_weights

4.残差连接和layernorm

4.1残差连接

在经过多头注意力处理后，我们的输出 \(Attention(Q,K,V)\) 的维度就是 \((batch\_size,seq\_len, d\_model)\) ，跟我们的原始属于 \(x\) 维度完全相等。因此我们这里可以直接使用残差连接，将他们加起来就得到 \((X + Attention(Q,K,V))\) 。

解决的问题：

网络退化并不是过拟合，过拟合是指~，网络退化是模型在训练数据集和测试集上面的表现都不好。
通常网络退化是由神经网络层数过多引起的（会造成梯度爆炸、消失；过拟合等问题）
解决方法：resnet中提出的残差连接的概念，首先我们知道，我们在训练网络时，网络层数越高理论上效果至少不会比层数较低时表现得更差（因为最后面的几层神经网络可以全都是identity mapping）。但事实上网络层数过深就会造成网络退化。为了解决这个问题，resnet中显式的构造出了一个identity mapping—让每层神经网络学习\(f(x):= H(x) - x\)，相当于在反向传播求导的时候加了一个恒等项。（其中X是上一层神经网络的输出，H(x)是这一层要学习的函数）最后该层神经网络的输出等价于上一层神经网络的输出x和这一层神经网络学习残差的输出之和。

4.2 layernorm

作用：跟batchnorm一样，加速模型收敛

不同的是LN是操作一个样本的所有特征，让各个特征的分布变为均值为0，方差为1。并且引入可训练系数 \(\alpha, \beta\) ，弥补归一化过程中损失的信息。
BN是对一个batch_size内的所有所有样本的同一特征进行归一化操作。

class EncoderLayer(tf.keras.layers.Layer):
  def __init__(self, d_model, num_heads, dff, rate=0.1):
    super(EncoderLayer, self).__init__()

    self.mha = MultiHeadAttention(d_model, num_heads)   
    self.ffn = point_wise_feed_forward_network(d_model, dff)  # 前向传播

    self.layernorm1 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
    self.layernorm2 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
    
    self.dropout1 = tf.keras.layers.Dropout(rate)
    self.dropout2 = tf.keras.layers.Dropout(rate)
    
  def call(self, x, training, mask):

    attn_output, _ = self.mha(x, x, x, mask)  # (batch_size, input_seq_len, d_model)  三个x代表上一层的输出，N个encoder是串联的
    attn_output = self.dropout1(attn_output, training=training)
    out1 = self.layernorm1(x + attn_output)  # (batch_size, input_seq_len, d_model) 残差连接
    
    ffn_output = self.ffn(out1)  # (batch_size, input_seq_len, d_model)
    ffn_output = self.dropout2(ffn_output, training=training)
    out2 = self.layernorm2(out1 + ffn_output)  # (batch_size, input_seq_len, d_model)
    
    return out2

5.FFN

就是一个两层的MLP模型。

相当于将多头注意力之后的输出 \(Attention(Q,K,V)\) 做一个非线性变换。因为我们之前的操作包括attention机制都是线性的，这里引入非线性因素，使模型更好收敛。

#@save
class PositionWiseFFN(tf.keras.layers.Layer):
    """基于位置的前馈网络"""
    def __init__(self, ffn_num_hiddens, ffn_num_outputs, **kwargs):
        super().__init__(*kwargs)
        self.dense1 = tf.keras.layers.Dense(ffn_num_hiddens)
        self.relu = tf.keras.layers.ReLU()
        self.dense2 = tf.keras.layers.Dense(ffn_num_outputs)

    def call(self, X):
        return self.dense2(self.relu(self.dense1(X)))

Decoder架构

针对于Encoder的不同来阐述：

1. Decoder的mask多注意力机制

这是因为不同于encoder的多头注意力机制用来抓取全局序列的信息，我Decoder是要用来预测下一个输出的，因此也就无法看到 \(t\) 时刻以及之后的语句序列。

2. Decoder中间的多头注意力

这里不再是自注意力机制，而是将encoder的输出拿过来作为 \(Key-Value\) 矩阵，与自己的第一层注意力输出矩阵做注意力运算。通过这种方式有效的提取encoder的输出。

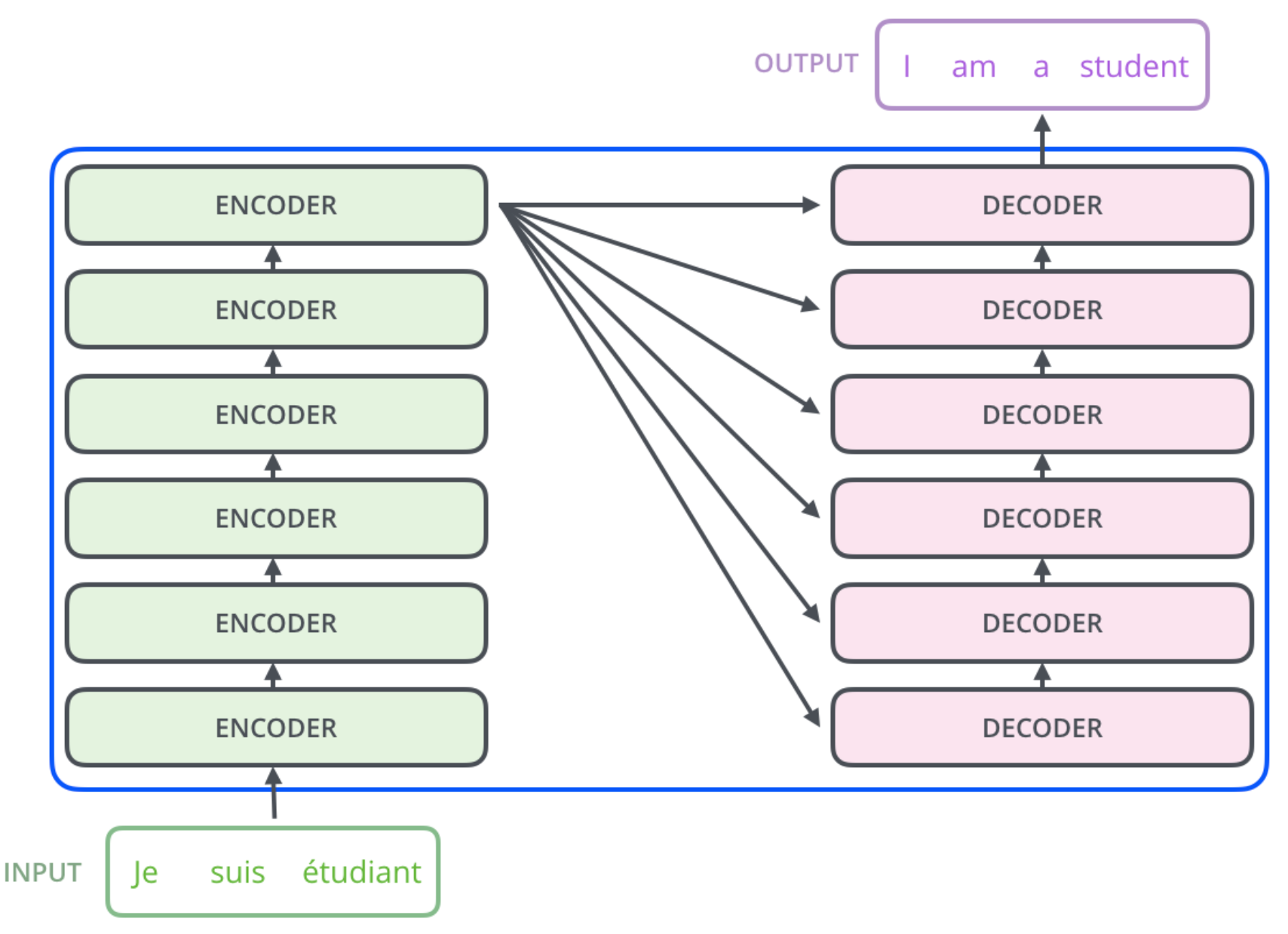
与RNN的异同

从输入的处理来看：RNN的输入序列中每个字都天然的按时间排序。transformer中则是用positional encoding给每个字附加上了位置信息。
从使用序列上一时刻的信息来看：RNN将上一时刻的隐藏状态作为下一时刻的输入，从而传递了之前时刻的信息。transformer是拿到整个句子的注意力输出，然后通过MLP找到我们想要的东西。
附上邱锡鹏老师书中的插图：几种不同的序列到序列模型

posted @ 2022-03-30 19:49 王子春阅读(69) 评论(0) 编辑收藏举报

刷新页面返回顶部

Loading

bhllssjdhj's Blog