高斯消元 分析 && 模板 （转载）

转载自：http://hi.baidu.com/czyuan_acm/item/dce4e6f8a8c45f13d7ff8cda czyuan

先上模板：

/* 用于求整数解得方程组. */
#include <iostream>
#include <string>
#include <cmath>
using namespace std;
const int maxn = 105;
int equ, var; // 有equ个方程，var个变元。增广阵行数为equ, 分别为0到equ - 1，列数为var + 1，分别为0到var.
int a[maxn][maxn];
int x[maxn]; // 解集.
bool free_x[maxn]; // 判断是否是不确定的变元.
int free_num;
void Debug(void)
{
    int i, j;
    for (i = 0; i < equ; i++)
    {
        for (j = 0; j < var + 1; j++)
        {
            cout << a[i][j] << " ";
        }
        cout << endl;
    }
    cout << endl;
}
inline int gcd(int a, int b)
{
    int t;
    while (b != 0)
    {
        t = b;
        b = a % b;
        a = t;
    }
    return a;
}
inline int lcm(int a, int b)
{
    return a * b / gcd(a, b);
}
// 高斯消元法解方程组(Gauss-Jordan elimination).(-2表示有浮点数解，但无整数解，-1表示无解，0表示唯一解，大于0表示无穷解，并返回自由变元的个数)
int Gauss(void)
{
    int i, j, k;
    int max_r; // 当前这列绝对值最大的行.
int col; // 当前处理的列.
    int ta, tb;
    int LCM;
    int temp;
    int free_x_num;
    int free_index;
    // 转换为阶梯阵.
    col = 0; // 当前处理的列.
    for (k = 0; k < equ && col < var; k++, col++)
    { // 枚举当前处理的行.
        // 找到该col列元素绝对值最大的那行与第k行交换.(为了在除法时减小误差)
        max_r = k;
        for (i = k + 1; i < equ; i++)
        {
            if (abs(a[i][col]) > abs(a[max_r][col])) max_r = i;
        }
        if (max_r != k)
        { // 与第k行交换.
            for (j = k; j < var + 1; j++) swap(a[k][j], a[max_r][j]);
        }
        if (a[k][col] == 0)
        { // 说明该col列第k行以下全是0了，则处理当前行的下一列.
            k--; continue;
        }
        for (i = k + 1; i < equ; i++)
        { // 枚举要删去的行.
            if (a[i][col] != 0)
    {
                LCM = lcm(abs(a[i][col]), abs(a[k][col]));
                ta = LCM / abs(a[i][col]), tb = LCM / abs(a[k][col]);
                if (a[i][col] * a[k][col] < 0) tb = -tb; // 异号的情况是两个数相加.
                for (j = col; j < var + 1; j++)
                {
                    a[i][j] = a[i][j] * ta - a[k][j] * tb;
                }
    }
        }
    }
    Debug();
    // 1. 无解的情况: 化简的增广阵中存在(0, 0, ..., a)这样的行(a != 0).
    for (i = k; i < equ; i++)
    { // 对于无穷解来说，如果要判断哪些是自由变元，那么初等行变换中的交换就会影响，则要记录交换.
        if (a[i][col] != 0) return -1;
    }
    // 2. 无穷解的情况: 在var * (var + 1)的增广阵中出现(0, 0, ..., 0)这样的行，即说明没有形成严格的上三角阵.
    // 且出现的行数即为自由变元的个数.
    if (k < var)
    {
        // 首先，自由变元有var - k个，即不确定的变元至少有var - k个.
        for (i = k - 1; i >= 0; i--)
        {
            // 第i行一定不会是(0, 0, ..., 0)的情况，因为这样的行是在第k行到第equ行.
            // 同样，第i行一定不会是(0, 0, ..., a), a != 0的情况，这样的无解的.
            free_x_num = 0; // 用于判断该行中的不确定的变元的个数，如果超过1个，则无法求解，它们仍然为不确定的变元.
            for (j = 0; j < var; j++)
            {
                if (a[i][j] != 0 && free_x[j]) free_x_num++, free_index = j;
            }
            if (free_x_num > 1) continue; // 无法求解出确定的变元.
            // 说明就只有一个不确定的变元free_index，那么可以求解出该变元，且该变元是确定的.
            temp = a[i][var];
            for (j = 0; j < var; j++)
            {
                if (a[i][j] != 0 && j != free_index) temp -= a[i][j] * x[j];
            }
            x[free_index] = temp / a[i][free_index]; // 求出该变元.
            free_x[free_index] = 0; // 该变元是确定的.
        }
        return var - k; // 自由变元有var - k个.
    }
    // 3. 唯一解的情况: 在var * (var + 1)的增广阵中形成严格的上三角阵.
    // 计算出Xn-1, Xn-2 ... X0.
    for (i = var - 1; i >= 0; i--)
    {
        temp = a[i][var];
        for (j = i + 1; j < var; j++)
        {
            if (a[i][j] != 0) temp -= a[i][j] * x[j];
        }
        if (temp % a[i][i] != 0) return -2; // 说明有浮点数解，但无整数解.
        x[i] = temp / a[i][i];
    }
return 0;
}
int main(void)
{
    freopen("Input.txt", "r", stdin);
    int i, j;
    while (scanf("%d %d", &equ, &var) != EOF)
    {
        memset(a, 0, sizeof(a));
   memset(x, 0, sizeof(x));
   memset(free_x, 1, sizeof(free_x)); // 一开始全是不确定的变元.
        for (i = 0; i < equ; i++)
        {
            for (j = 0; j < var + 1; j++)
            {
                scanf("%d", &a[i][j]);
            }
        }
//        Debug();
        free_num = Gauss();
        if (free_num == -1) printf("无解!\n");
   else if (free_num == -2) printf("有浮点数解，无整数解!\n");
        else if (free_num > 0)
        {
            printf("无穷多解! 自由变元个数为%d\n", free_num);
            for (i = 0; i < var; i++)
            {
                if (free_x[i]) printf("x%d 是不确定的\n", i + 1);
                else printf("x%d: %d\n", i + 1, x[i]);
            }
        }
        else
        {
            for (i = 0; i < var; i++)
            {
                printf("x%d: %d\n", i + 1, x[i]);
            }
        }
        printf("\n");
    }
    return 0;
}

 

高斯消元法，是线性代数中的一个算法，可用来求解线性方程组，并可以求出矩阵的秩，以及求出可逆方阵的逆矩阵。
高斯消元法的原理是：
若用初等行变换将增广矩阵 化为 ，则AX = B与CX = D是同解方程组。
所以我们可以用初等行变换把增广矩阵转换为行阶梯阵，然后回代求出方程的解。

以上是线性代数课的回顾，下面来说说高斯消元法在编程中的应用。

首先，先介绍程序中高斯消元法的步骤：
(我们设方程组中方程的个数为equ，变元的个数为var，注意：一般情况下是n个方程，n个变元，但是有些题目就故意让方程数与变元数不同)

1. 把方程组转换成增广矩阵。

2. 利用初等行变换来把增广矩阵转换成行阶梯阵。
枚举k从0到equ – 1，当前处理的列为col(初始为0) ，每次找第k行以下(包括第k行)，col列中元素绝对值最大的列与第k行交换。如果col列中的元素全为0，那么则处理col + 1列，k不变。

3. 转换为行阶梯阵，判断解的情况。

① 无解
当方程中出现(0, 0, …, 0, a)的形式，且a != 0时，说明是无解的。

② 唯一解
条件是k = equ，即行阶梯阵形成了严格的上三角阵。利用回代逐一求出解集。

③ 无穷解。
条件是k < equ，即不能形成严格的上三角形，自由变元的个数即为equ – k，但有些题目要求判断哪些变元是不缺定的。
    这里单独介绍下这种解法：
首先，自由变元有var - k个，即不确定的变元至少有var - k个。我们先把所有的变元视为不确定的。在每个方程中判断不确定变元的个数，如果大于1个，则该方程无法求解。如果只有1个变元，那么该变元即可求出，即为确定变元。

以上介绍的是求解整数线性方程组的求法，复杂度是O(n3)。浮点数线性方程组的求法类似，但是要在判断是否为0时，加入EPS，以消除精度问题。

下面讲解几道OJ上的高斯消元法求解线性方程组的题目：

POJ 1222 EXTENDED LIGHTS OUT
http://acm.pku.edu.cn/JudgeOnline/problem?id=1222
POJ 1681 Painter's Problem
http://acm.pku.edu.cn/JudgeOnline/problem?id=1681
POJ 1753 Flip Game
http://acm.pku.edu.cn/JudgeOnline/problem?id=1753
POJ 1830 开关问题
http://acm.pku.edu.cn/JudgeOnline/problem?id=1830

POJ 3185 The Water Bowls

http://acm.pku.edu.cn/JudgeOnline/problem?id=3185
开关窗户，开关灯问题，很典型的求解线性方程组的问题。方程数和变量数均为行数*列数，直接套模板求解即可。但是，当出现无穷解时，需要枚举解的情况，因为无法判断哪种解是题目要求最优的。

POJ 2947 Widget Factory
http://acm.pku.edu.cn/JudgeOnline/problem?id=2947
求解同余方程组问题。与一般求解线性方程组的问题类似，只要在求解过程中加入取余即可。
注意：当方程组唯一解时，求解过程中要保证解在[3, 9]之间。

POJ 1166 The Clocks
http://acm.pku.edu.cn/JudgeOnline/problem?id=1166
经典的BFS问题，有各种解法，也可以用逆矩阵进行矩阵相乘。
但是这道题用高斯消元法解决好像有些问题(困扰了我N天...持续困扰中...)，由于周期4不是素数，故在求解过程中不能进行取余(因为取余可能导致解集变大)，但最后求解集时，还是需要进行取余操作，那么就不能保证最后求出的解是正确的...在discuss里提问了好几天也没人回答...希望哪位路过的大牛指点下～～

POJ 2065 SETI
http://acm.pku.edu.cn/JudgeOnline/problem?id=2065
同样是求解同余方程组问题，由于题目中的p是素数，可以直接在求解时取余，套用模板求解即可。(虽然AC的人很少，但它还是比较水的一道题，)

POJ 1487 Single-Player Games
http://acm.pku.edu.cn/JudgeOnline/problem?id=1487
很麻烦的一道题目...题目中的叙述貌似用到了编译原理中的词法定义(看了就给人不想做的感觉...)
解方程组的思想还是很好看出来了(前提是通读题目不下5遍...)，但如果把树的字符串表达式转换成方程组是个难点，我是用栈 + 递归的做法分解的。首先用栈的思想求出该结点的孩子数，然后递归分别求解各个孩子。
这题解方程组也与众不同...首先是求解浮点数方程组，要注意精度问题，然后又询问不确定的变元，按前面说的方法求解。
一顿折腾后，这题居然写了6000+B...而且囧的是巨人C++ WA，G++ AC，可能还是精度的问题吧...看这题目，看这代码，就没有改的欲望...

hdu OJ 2449
http://acm.hdu.edu.cn/showproblem.php?pid=2449
哈尔滨现场赛的一道纯高斯题，当时鹤牛敲了1个多小时...主要就是写一个分数类，套个高精模板(偷懒点就Java...)搞定～～
注意下0和负数时的输出即可。

fze OJ 1704
http://acm.fzu.edu.cn/problem.php?pid=1704
福大月赛的一道题目，还是经典的开关问题，但是方程数和变元数不同(考验模板的时候到了～～)，最后要求增广阵的阶，要用到高精度～～

Sgu 275 To xor or not to xor
http://acm.sgu.ru/problem.php?contest=0&problem=275
题解:
http://hi.baidu.com/czyuan%5Facm/blog/item/be3403d32549633d970a16ee.html

这里提供下自己写的还算满意的求解整数线性方程组的模板(浮点数类似，就不提供了)～～

 

 

下面的总结转载自： 英雄哪里出来  这篇博客写的也非常不错，里面有对高斯消元好多题目的思路详解，强力推荐！

高斯消元

算法目的：
            高斯消元，一般用于求解线性方程组AX = B（或 模线性方程组AX mod P = B），以四个未知数，四个方程为例，AX=B表示成4x4的矩        阵和4x1的矩阵相乘的形式：  

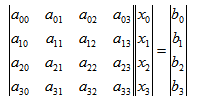
其中A和B(b0 b1 b2 b3)已知，要求列向量X(x0 x1 x2 x3)的值。

算法核心思想：
            对于n个方程，m个未知数的方程组，消元的具体步骤如下：

1、枚举第i (0 <= i < n) 行，初始化列为col = 0，每次从[i, n)行中找到第col列中元素绝对值最大的行和第i行进行交换(找到最大的行是为了在消元的时候把浮点数的误差降到最小)；

a) 如果第col列的元素全为0，放弃这一列的处理，col+1，i不变，转1)；

b) 否则，对于所有的行j (i < j < n)，如果a[j][col]不为0，则需要进行消元，以期第i行以下的第col列的所有元素都消为0（这一步就是线性代数中所说的初等行变换，具体的步骤就是将第j行的所有元素减去第i行的所有元素乘上一个系数，这个系数即a[j][col] / a[i][col]）。

2、重复步骤1) 直到n个方程枚举完毕或者列col == m。

3、判断解的情况：

a) 如果出现某一行，系数矩阵全为0，增广矩阵不全为0，则无解（即出现[0 0 0 0 0 b]，其中b不等于0的情况）；

b) 如果是严格上三角，则表明有唯一解；

c) 如果增广矩阵有k (k > 0)行全为0，那么表明有k个变量可以任意取值，这几个变量即自由变量；对于这种情况，一般解的范围是给定的，令解的取值有T个，自由变量有V个，那么解的个数就是 TV。

算法复杂度：
      O(n³)

ACM中的高斯消元题型一般涉及到的有：

1、浮点数消元

系数矩阵为整数或浮点数，消元的时候乘上的系数为浮点数，一般用于求解浮点数解，例如HDU 3359；

2、整数消元

系数矩阵全为整数，消元的时候乘上的系数均为整数，整个消元过程不出现浮点数。由于乘法很容易溢出，一般很少用。

3、模线性方程组

系数矩阵全为整数，消元的时候乘上的系数均为整数，每次运算都模上一个数P，整个消元过程不出现除法，最后求解的时候用线性同余迭代求解，一般题型较多，有的是给定解的范围，求解的数量，例如：PKU 1830、HDU 3364；有的是求一个解，例如PKU 2065、HDU 3571；有的是求解的存在性，例如PKU1288、PKU 3185。