决策树

决策树基本上就是把我们以前的经验总结出来。这里有一个打篮球的训练集。假如我们要出门打篮球，一般会根据“天气”、“温度”、“湿度”、“刮风”这几个条件来判断，最后得到结果：去打篮球？还是不去？

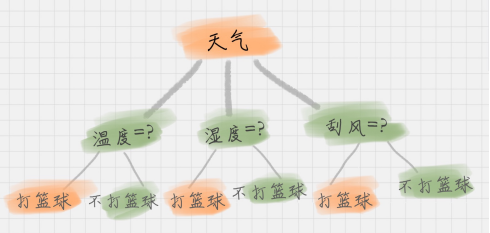
上面这个图就是一棵典型的决策树。我们在做决策树的时候，会经历两个阶段：构造和剪枝。

 

构造

什么是构造呢？构造就是生成一棵完整的决策树。简单来说，构造的过程就是选择什么属性作为节点的过程，那么在构造过程中，会存在三种节点：

1.根节点：就是树的最顶端，最开始的那个节点。在上图中，“天气”就是一个根节点；

2.内部节点：就是树中间的那些节点，比如说“温度”、“湿度”、“刮风”；

3.叶节点：就是树最底部的节点，也就是决策结果。

节点之间存在父子关系。比如根节点会有子节点，子节点会有子子节点，但是到了叶节点就停止了，叶节点不存在子节点。那么在其实构造就是对应着三个重要的问题：

1.选择哪个属性作为根节点；

2.选择哪些属性作为子节点；

3.什么时候停止并得到目标状态，即叶节点。

 

剪枝

决策树构造出来之后是不是就万事大吉了呢？也不尽然，我们可能还需要对决策树进行剪枝。剪枝就是给决策树瘦身，这一步想实现的目标就是，不需要太多的判断，同样可以得到不错的结果。之所以这么做，是为了防止“过拟合”（Overfitting）现象的发生。过拟合，它指的就是模型的训练结果“太好了”，以至于在实际应用的过程中，会存在“死板”的情况，导致分类错误。

那么如何解决刚才构造的三个问题呢？

第三个问题叶节点一般就是对应我们的目标，比如去或者不去

而前两个问题可以合并成一个问题，那就是以最重要特征作为根节点、以此类推

那么如何计算特征的重要性呢？这里就需要用到信息熵这个概念：它表示了信息的不确定度。

 

 

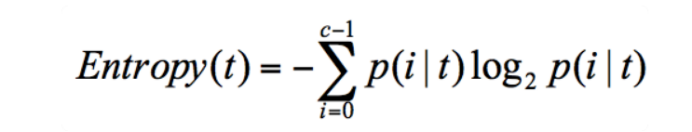
def entropy(elements):
    """
    计算熵
    (各个元素出现次数/总数 * （各个元素出现次数/总数）的对数)的总数取负
    :param elements:
    :return:
    """
    counter = Counter(elements)
    probs = [counter[c] / len(elements) for c in elements]
    return - sum(p * np.log(p) for p in probs)

 

假设有 2 个集合

集合 1：5 次去打篮球，1 次不去打篮球；

集合 2：3 次去打篮球，3 次不去打篮球。

在集合 1 中，有 6 次决策，其中打篮球是 5 次，不打篮球是 1 次。那么假设：类别 1 为“打篮球”，即次数为 5；类别 2 为“不打篮球”，即次数为 1。那么节点划分为类别 1 的概率是 5/6，为类别 2 的概率是 1/6，带入上述信息熵公式可以计算得出：

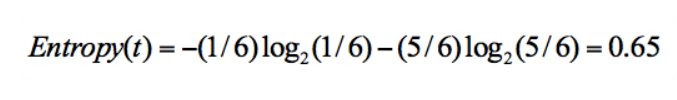
同样，集合 2 中，也是一共 6 次决策，其中类别 1 中“打篮球”的次数是 3，类别 2“不打篮球”的次数也是 3，那么信息熵为多少呢？我们可以计算得出：

 

 

 

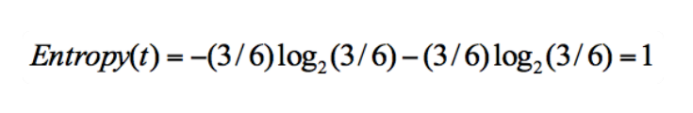
很明显，如果按某特征区分后，样本越均匀，则信息熵越大。相反如果某特征带来的信息熵越小，那么它越好的，我们确定根节点则需要找到这个信息熵最小的节点就是了。

 

 

def find_the_min_spilter(training_data: pd.DataFrame, target: str) -> str:
    """
    寻找分割后最小熵的分割特征
    :param training_data: 数据
    :param target: 目标特征
    :return:
    """
    # 将数据去除目标特征
    x_fields = set(training_data.columns.tolist()) - {target}

    spliter = None
    min_entropy = float('inf')          # 预先设置成正无穷

    for f in x_fields:                  # 循环所有特征名
        values = set(training_data[f])  # 取该特征所有数值做集合
        for v in values:                # 循环该特征所有数值集合
            sub_spliter_1 = training_data[training_data[f] == v][target].tolist()       # 计算等于该数值对目标特征分布
            entropy_1 = entropy(sub_spliter_1)                                          # 计算等于该数值时目标特征分布信息熵
            sub_spliter_2 = training_data[training_data[f] != v][target].tolist()       # 计算不等于该数值对目标特征分布
            entropy_2 = entropy(sub_spliter_2)                                          # 计算不等于该数值时目标特征分布信息熵
            entropy_v = entropy_1 + entropy_2                                           # 计算此数值对目标特征的总信息熵

            if entropy_v <= min_entropy:        # 如果信息熵小于当前最小信息熵则更新信息熵与特征
                min_entropy = entropy_v
                spliter = (f, v)

    print('spliter is: {}'.format(spliter))
    print('the min entropy is: {}'.format(min_entropy))
    print('----------------------')

    return spliter