每日一题 LeetCode 486. 预测赢家 【递推】【前缀和】【动态规划】
题目链接
https://leetcode-cn.com/problems/predict-the-winner/
题目说明
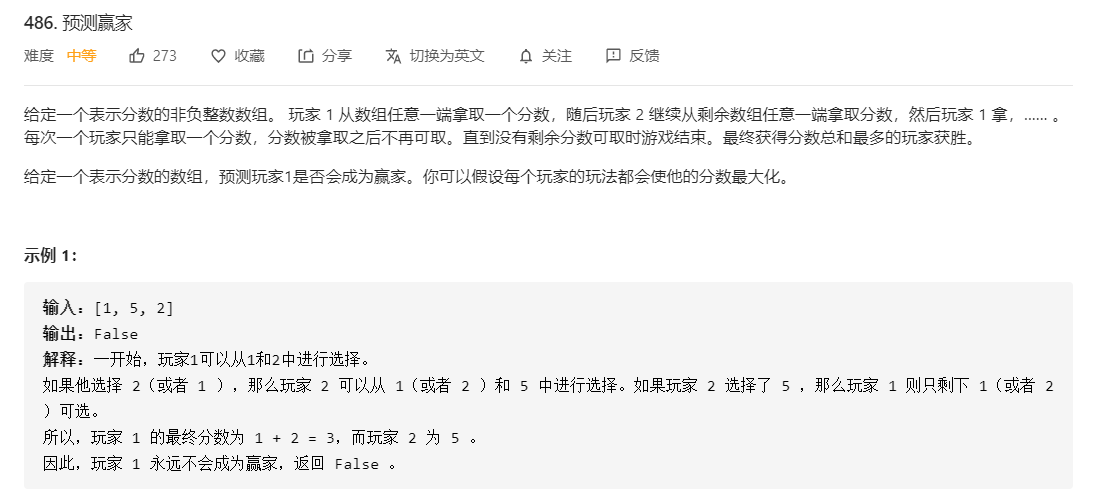
题解
主要方法:递推;动态规划;前缀和
解释说明:
-
求前缀和 pre_nums ,pre_nums[0] = 0, pre_nums[1+i] = sum(nums[0……i])
-
动态规划、递推:
- 数据表示:设立二维数组dp,dp[i][j]表示区间 [i,j] 内先取者能取得的最大值。dpnums
- 初始状态:遍历 nums 数组求得长度为 1 的区间 [i,i] 内的最大值,即 dp[i][i] = nums[i]
- 动态方程:先后遍历长度l,起点i,dp[i][j] [i,j]内最大值 = pre_nums[j+1]-pre_nums[i] nums[i,j]的总和 - min(dp[i][j-1] 取尾端,则减去下一个人相应的最大值[i,j-1], dp[i+1][j]) 取首端,则减去下一个人相应的最大值[i+1,j];
-
数据输出:比较全部最大值与总和的一半 return dp[0][size-1] >= sum/2
代码示例:
class Solution:
def PredictTheWinner(self, nums: List[int]) -> bool:
size = len(nums)
# 求前缀和
pre_nums = [0]
for i in range(size):
pre_nums.append(pre_nums[-1]+nums[i])
dp, tmp = nums[:], []
# 动态规划,这里 dp 数组降维,重复使用
for l in range(2, size+1):
tmp.clear()
for i in range(size - l + 1):
tmp.append(pre_nums[i+l] - pre_nums[i] - min(dp[i], dp[i+1]))
dp = tmp[:]
return dp[0] >= pre_nums[-1]/2

