CPM(Cluster Percolation method)派系过滤算法
一、概念
(1)完全子图/全耦合网络/k-派系:所有节点全部两两相连
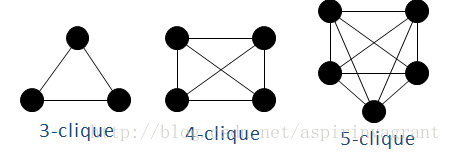
图1
这些全耦合网络也成为派系,k-派系表示该全耦合网络的节点数目为k
1)k-派系相邻:两个不同的k-派系共享k-1个节点,认为他们相邻
2)k-派系连通:一个k-派系可以通过若干个相邻的k-派系到达另一个k-派系,则称这两个k-派系彼此联通
二、思路
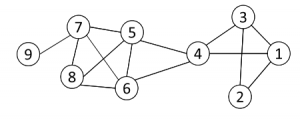
图2
1- first find all cliques of size k in the graph
第一步首先找到网络中大小为K的完全子图,例如图2中k=3的完全子图有{1, 2, 3} {1, 3, 4} {4, 5, 6} {5, 6, 7} {5, 6, 8} {5, 7, 8} {6, 7, 8}
2- then create graph where nodes are cliques of size k
第二步将每个完全子图定义为一个节点,建立一个重叠矩阵
a=[3 2 0 0 0 0 0;
2 3 1 0 0 0 0;
0 1 3 2 2 1 1;
0 0 2 3 2 2 2;
0 0 2 2 3 2 2;
0 0 1 2 2 3 2;
0 0 1 2 2 2 3 ]
3- add edges if two nodes (cliques) share k-1 common nodes
第三步将重叠矩阵变成社团邻接矩阵,其中重叠矩阵中对角线小于k,非对角线小于k-1的元素全置为0
a=[1 1 0 0 0 0 0;
1 1 0 0 0 0 0;
0 0 1 1 1 0 0;
0 0 1 1 1 1 1;
0 0 1 1 1 1 1;
0 0 0 1 1 1 1;
0 0 0 1 1 1 1 ]
4- each connected component is a community
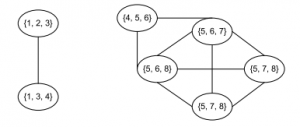
画出派系图,如上所示
从图中可以看出包含了两个社区{1,2,3,4}和{4,5,6,7,8},节点4属于两个社区的重叠节点
三、代码实现
R实现代码和Java实现代码可在GitHub网站上下载,R下载地址
https://github.com/angelosalatino/CliquePercolationMethod-R
四、References
Palla, G., Derényi, I., Farkas, I., & Vicsek, T. (2005). Uncovering the overlapping community structure of complex networks in nature and society. Nature, 435(7043), 814-818.
注意事项:
CPM算法不适用于稀疏矩阵,K的取值对结果影响不大,一般实验证明4-6为最佳
2017年4.16更新
用matlab算法实现,其中做了一点小变动,k是最小派系范围,寻找的是大于等于k的完全子图数,得到结果与上述描述结果一致,节点4是重叠节点
function [components,cliques,CC] = k_clique(k,M)
% k-clique algorithm for detecting overlapping communities in a network
% as defined in the paper "Uncovering the overlapping
% community structure of complex networks in nature and society" -
% G. Palla, I. Derényi, I. Farkas, and T. Vicsek - Nature 435, 814–818 (2005)
%
% [X,Y,Z] = k_clique(k,A)
%
% Inputs:
% k - clique size
% A - adjacency matrix
%
% Outputs:
% X - detected communities
% Y - all cliques (i.e. complete subgraphs that are not parts of larger
% complete subgraphs)
% Z - k-clique matrix
%
% Author : Anh-Dung Nguyen
% Email : anh-dung.nguyen@isae.fr
% The adjacency matrix of the example network presented in the paper
% M = [1 1 0 0 0 0 0 0 0 1;
% 1 1 1 1 1 1 1 0 0 1;
% 0 1 1 1 0 0 1 0 0 0;
% 0 1 1 1 1 1 1 0 0 0;
% 0 1 0 1 1 1 1 1 0 0;
% 0 1 0 1 1 1 1 1 0 0;
% 0 1 1 1 1 1 1 1 1 1;
% 0 0 0 0 1 1 1 1 1 1;
% 0 0 0 0 0 0 1 1 1 1;
% 1 1 0 0 0 0 1 1 1 1];
nb_nodes = size(M,1); % number of nodes
% Find the largest possible clique size via the degree sequence:
% Let {d1,d2,...,dk} be the degree sequence of a graph. The largest
% possible clique size of the graph is the maximum value k such that
% dk >= k-1
degree_sequence = sort(sum(M,2) - 1,'descend');
max_s = 0;
for i = 1:length(degree_sequence)
if degree_sequence(i) >= i - 1
max_s = i;
else
break;
end
end
cliques = cell(0);
% Find all s-size kliques in the graph
for s = max_s:-1:3
M_aux = M;
% Looping over nodes
for n = 1:nb_nodes
A = n; % Set of nodes all linked to each other
B = setdiff(find(M_aux(n,:)==1),n); % Set of nodes that are linked to each node in A, but not necessarily to the nodes in B
C = transfer_nodes(A,B,s,M_aux); % Enlarging A by transferring nodes from B
if ~isempty(C)
for i = size(C,1)
cliques = [cliques;{C(i,:)}];
end
end
M_aux(n,:) = 0; % Remove the processed node
M_aux(:,n) = 0;
end
end
% Generating the clique-clique overlap matrix
CC = zeros(length(cliques));
for c1 = 1:length(cliques)
for c2 = c1:length(cliques)
if c1==c2
CC(c1,c2) = numel(cliques{c1});
else
CC(c1,c2) = numel(intersect(cliques{c1},cliques{c2}));
CC(c2,c1) = CC(c1,c2);
end
end
end
% Extracting the k-clique matrix from the clique-clique overlap matrix
% Off-diagonal elements <= k-1 --> 0
% Diagonal elements <= k --> 0
CC(eye(size(CC))==1) = CC(eye(size(CC))==1) - k;
CC(eye(size(CC))~=1) = CC(eye(size(CC))~=1) - k + 1;
CC(CC >= 0) = 1;
CC(CC < 0) = 0;
% Extracting components (or k-clique communities) from the k-clique matrix
components = [];
for i = 1:length(cliques)
linked_cliques = find(CC(i,:)==1);
new_component = [];
for j = 1:length(linked_cliques)
new_component = union(new_component,cliques{linked_cliques(j)});
end
found = false;
if ~isempty(new_component)
for j = 1:length(components)
if all(ismember(new_component,components{j}))
found = true;
end
end
if ~found
components = [components; {new_component}];
end
end
end
function R = transfer_nodes(S1,S2,clique_size,C)
% Recursive function to transfer nodes from set B to set A (as
% defined above)
% Check if the union of S1 and S2 or S1 is inside an already found larger
% clique
found_s12 = false;
found_s1 = false;
for c = 1:length(cliques)
for cc = 1:size(cliques{c},1)
if all(ismember(S1,cliques{c}(cc,:)))
found_s1 = true;
end
if all(ismember(union(S1,S2),cliques{c}(cc,:)))
found_s12 = true;
break;
end
end
end
if found_s12 || (length(S1) ~= clique_size && isempty(S2))
% If the union of the sets A and B can be included in an
% already found (larger) clique, the recursion is stepped back
% to check other possibilities
R = [];
elseif length(S1) == clique_size;
% The size of A reaches s, a new clique is found
if found_s1
R = [];
else
R = S1;
end
else
% Check the remaining possible combinations of the neighbors
% indices
if isempty(find(S2>=max(S1),1))
R = [];
else
R = [];
for w = find(S2>=max(S1),1):length(S2)
S2_aux = S2;
S1_aux = S1;
S1_aux = [S1_aux S2_aux(w)];
S2_aux = setdiff(S2_aux(C(S2(w),S2_aux)==1),S2_aux(w));
R = [R;transfer_nodes(S1_aux,S2_aux,clique_size,C)];
end
end
end
end
end


 浙公网安备 33010602011771号
浙公网安备 33010602011771号