序列数据波峰识别以及波峰形状识别
转载请注明出处:https://www.cnblogs.com/bethansy/p/10560341.html
1、波峰识别
序列数据是按照时间进行采集,其中400个点一个周期,一条数据共10个周期,即4000个点。 首先针对序列数据判断每个周期是否存在波峰,并在存在波峰的情况下进行波峰形状识别。 其中波峰识别主要遍历寻找某个值既大于左边又大于右边
1.1、参数:
①peak_thre:获取时域振动数据95%(20/400)分位数值大小,将此值得0.8倍作为波峰阈值
②peak_width:数据中间隔15个点及其以内的波峰被识别为一个波峰
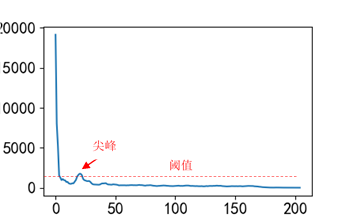
图1.1 波峰识别逻辑
1.2、算法原理:
data[i-1]<data[i] & data[i]>data[i+1] & data[i]> peak_thre
OR
data[i-1]=data[i] & data[i]> peak_thre
1.3、步骤
(1)平滑处理序列数据
(2)波峰个数识别
1.4、返回值
(1)N:一条时域数据中波峰个数
(2)peak_index:每个波峰对应的索引值

图1.2 数据平滑处理
算法处理后,共识别出10个波峰,每个波峰对应的索引分别为[37,77,117,157,197,237,277,317,357,397]
2、波峰形状识别
这里波峰形状主要是指等腰三角形和直角三角形,三角形原理
1、参数
①peak_index:上一节获得的每个波峰的索引
②noise_ratio:为便于计算每个三角形的占空比,默认为每圈最大值的0.2或0.3作为滤噪基数,低于以下的值当做0处理。
2、算法原理
如图2.2所示的两种形式会被识别为直角三角形:2.2-a(左边宽度大于右边宽度,且占空比小于0.2),2.2-b(右边宽度大于左边,且占空比小于0.3)。其中占比0.2和0.3是根据大量数据案例统计得到。

2.2-a 2.2-b
图2.2 识别为直角三角形的两种形式
3、步骤
(1)将时域数据每一圈故障波形进行降噪处理
(2)每个波形占空比计算
(3)识别每个波峰三角形形状,统计一条振动数据出现次数最多的三角形形状作为每个故障波形三角形形状输出结果。
4、返回值
(1)flag:三角形形状判断输出
(2)zanbi:每个三角形的占空比
以图2.2中时序列数据为例,输出结果为内部缺陷,每个三角形占空比分别为
[ 0.07, 0.0, 0.2, 0.125, 0.125, 0.175, 0.3, 0.4, 0.1, 0.39]
3、代码实现
# 波峰个数判别
def find_peak_triangleNum(filter_signal, peak_width):
'''
判断序列数据波形的三角形个数
:param filter_signal: 平滑后的波形
:param step:连续几个
:param peak_width:尖峰之间的宽距小于peak_width时划分为一个峰,频域数据一般定义在20;
时域数据三角形识别一般定义在15,太大会滤掉双峰
:return:
'''
# 判断是否有凸起
length_data = len(filter_signal)
thre = 0.7*np.percentile(filter_signal, 95) # 设置阈值高度 95%是前400个点的20个波峰点
# 在整个区域内找极值
l = []
for i in range(1,length_data-1):
if filter_signal[i-1] < filter_signal[i] and filter_signal[i]>filter_signal[i+1] and filter_signal[i]>thre:
l.append(i)
elif filter_signal[i] == filter_signal[i-1] and filter_signal[i]>thre:
l.append(i) # 最高点前后可能有相等的情况
CC = len(l) # 统计极值得个数
cou = 0
ll = l.copy()
for j in range(1, CC):
if l[j]-l[j-1] < peak_width: # 此判断用于将位于同一个峰内的极值点去掉
if l[j] > l[j-1]: # 同一个峰内的数据,将小的值替换成0
ll[j-1] = 0
else:
ll[j] = 0
cou = cou+1
rcou = CC -cou
ll = [i for i in ll if i > 0] # 去掉0的值
peak_index = []
# 找到每个区间内波峰最大值
# 截断每个区间再求区间最大值的索引
for i in range(len(ll)):
if i == 0:
index_range = np.array(l)[np.array(l) <= ll[i]]
else:
index_range = np.array(l)[(np.array(l)<=ll[i]) &(np.array(l)>ll[i-1])]
# 找到每个区间最大值得索引
peak_index.append(index_range[np.argmax(filter_signal[index_range],axis=0)])
return [rcou,peak_index]
# 三角形形状判别
def triangle_flag_meiquan(q_flush, n, ratio,max_index):
'''
判断三角形的形状,首先每400个点进行一次过滤,过滤的规则是value-max(value)*0.1
:param q_flush:
:param n: 一条振动数据包含的数据点数
:param ratio: 默认0.2或者0.3
:return:
'''
circle_range = [0]
zhankongbi = []
left = []
right = []
# 生成int_num*step 的矩阵,头尾需要判断 ,其中q_flush是list类型。
for i in range(len(max_index)-1):
next_index = int((max_index[i+1]-max_index[i])/2)+max_index[i]
circle_range.append(next_index)
q = q_flush[circle_range[i]:circle_range[i+1]]
# 每圈除噪
newq = q-max(q)*ratio
newq[newq < 0] = 0
# 占空比计算三角形形状判断
zhankongbi.append((max(max(np.where(newq > 0))) - min(min(np.where(newq > 0)))) /len(newq))
max_index_now = np.argmax(newq)
left.append(max_index_now - min(min(np.where(newq > 0))))
right.append(max(max(np.where(newq>0))) - max_index_now)
# 进行三角形识别,不考虑左边为0
right_zb = np.array(zhankongbi)[np.where(np.array(right) >= np.array(left))] # 右边大于等于左边对应占空比
right_count = np.sum(right_zb <= 0.3) # 右边大于左边占空比小于0.3的个数
left_zb = np.array(zhankongbi)[np.where(np.array(left) > np.array(right))] # 左边大于等于右边对应占空比
left_count = np.sum(left_zb <= 0.2) # 左边大于右边但是占空比小于0.2
if left_count+right_count >= len(zhankongbi)/2:
flag = 2 # 直角三角形
else:
flag = 1 # 等腰三角形
return [flag, zhankongbi]
# 平滑曲线(滤波)
def smooth(a,WSZ):
'''
:param a: 原始数据,NumPy 1-D array containing the data to be smoothed
必须是1-D的,如果不是,请使用 np.ravel()或者np.squeeze()转化
:param WSZ: smoothing window size needs, which must be odd number
:return:
'''
out0 = np.convolve(a,np.ones(WSZ,dtype=int),'valid')/WSZ
r = np.arange(1,WSZ-1,2)
start = np.cumsum(a[:WSZ-1])[::2]/r
stop = (np.cumsum(a[:-WSZ:-1])[::2]/r)[::-1]
return np.concatenate((start, out0, stop))


 浙公网安备 33010602011771号
浙公网安备 33010602011771号