西安交通大学 优化方法 大作业2 等式约束优化问题
写在最前面:如果你还没有在选课端选择这门课或是选课端还在开放时间段,强烈建议退选优化方法并换选数学建模
1 实验内容

2 实验方法
2.1 标准牛顿方法

2.2 不可行初始点Newton方法

2.3 对偶牛顿方法
首先确定当前优化问题的对偶问题,在通过标准Newton方法求解即可

3 算法实现
环境:matlab 2021a
main.m和三个Func.m分别实现三种牛顿方法
3.1 标准牛顿方法
for IterK=1:MaxTime
Grad=log(xk)+1; %计算梯度
Hessian=diag(1./xk); %计算Hessian矩阵
Rans=[Hessian,A';A,zeros(p,p)]\[-Grad;zeros(p,1)];%计算Dnt方向和对偶变量
Xnt=Rans(1:n); %计算Dnt\牛顿方向
Lamb_squre=(Xnt'*Hessian*Xnt); %计算牛顿减小量的平方
output(IterK)=xk'*log(xk); %计算目标函数的最优值
%停止准则:
if Lamb_squre<=2*err
break;
end
%回溯直线搜索
t=1;
while (min(xk+t*Xnt)<=0)
t=beta*t;
end
while (xk+t*Xnt)'*log(xk+t*Xnt)>=(xk)'*log(xk)+alpha*t*Grad'*Xnt%回溯
t=beta*t;
end
xk=xk+t*Xnt;
end
3.2 不可行初始点Newton方法
for IterK=1:MaxTime
Grad=log(xk)+1; %计算函数的梯度
Hessian=diag(1./xk); %计算函数的Hessian矩阵
r=[Grad+A'*dk;A*(xk)-b]; %原对偶残差
output(IterK)=xk'*log(xk); %输出目标函数值
Rans=-[Hessian,A';A,zeros(p,p)]\r; %求解牛顿方向和对偶变量
xnt=Rans(1:n); %求解Newton方向Dnt
dnt=Rans(n+1:n+p); %求解对偶变量
%停止准则:
if norm(r)<=err
break;
end
%对原多残差||r||2进行回溯,确定步长tk
t=1;
while (min(xk+t*xnt)<=0) %使x在定义域内
t=beta*t;
end
%回溯直线搜索停止准则
while norm([log(xk+t*xnt)+1+A'*(dk+t*dnt);A*(xk+t*xnt)-b])>(1-alpha*t)*norm(r)
t=beta*t;
end
xk=xk+t*xnt;
dk=dk+t*dnt;
end
3.3 对偶牛顿方法
for IterK=1:MaxTime
Grad=b-A*exp(-A'*v-1); %计算梯度
Hesssian=A*diag(exp(-A'*v-1))*A'; %计算Hessian矩阵
vnt=-Hesssian\Grad; %计算牛顿方向dnt
Lamd_square=Grad'*(Hesssian^-1)*Grad; %计算牛顿减小量λ
output(IterK)=b'*v+sum(exp(-A'*v-1)); %计算目标函数值最优值
%停止准则:
if Lamd_square<=2*err
break;
end
%回溯直线搜索
t=1;
while b'*(v+t*vnt)+sum(exp(-A'*(v+t*vnt)-1))>=b'*v+sum(exp(-A'*v-1))+alpha*t*Grad'*vnt
t=beta*t;
end
v=v+t*vnt;
end
3.4 主函数
%% 优化方法大作业 第三题
% 调用方法Func1,Func2,Func3
% Func1:标准newton方法
% Func2:出发点不可行newton方法
% Func3:对偶newton方法
% 输出1:随机生成的矩阵A、向量x
% 输出2:不同方法求解的最优值
% 输出3:不同方法对应求解问题的迭代次数
% 输出4:不同方法下误差随迭代次数增加的变化
%% 初始化,生成实例 随机选择矩阵A、正向量x
clear
clc
n=100; %A矩阵的列数
p=30; %A矩阵的行数
A=randn(p,n); %随机生成矩阵A
RA=rank(A);
while RA ~= p %判断矩阵的秩,直到符合要求为止
fprintf('A不是满秩矩阵,重新生成A\n');
A=randn(p,n);
end
fprintf('A是满秩矩阵,继续程序!\n');
x=rand(n,1); %生成向量x在[0,1]上均匀分布
b=A*x; %生成b
%% 初始化参数
% α=0.01,β=0.5 误差阈值ε=10^(-8),最大迭代次数MaxIter=100
alpha=0.01; %设置阿尔法
beta=0.5; %设置β值
yita=10^(-8); %设置阈值
MaxIter=100; %最大迭代次数
%% 标准Newton方法
fprintf('\n')
fprintf('标准Newton方法:')
fprintf('\n')
figure(1)
[figure0,calTime0]=Func1(x,MaxIter,yita,alpha,beta,A,b,p,n,'bo-');
title('标准Newton方法');
%% 不可行初始点Newton方法
fprintf('\n')
fprintf('不可行初始点Newton方法:')
fprintf('\n')
figure(2)
fprintf("初始点为x0=x:\n")
[figure1,calTime1]=Func2(x,zeros(p,1),MaxIter,yita,alpha,beta,A,b,p,n,'bo-');
hold on
fprintf("初始点为x0=1:\n")
[figure2,calTime2]=Func2(ones(n,1),zeros(p,1),MaxIter,yita,alpha,beta,A,b,p,n,'r*-');
title('不可行初始点Newton方法');
legend([figure1,figure2],'初始点为X0=x','初始点为x0=1');
%% 对偶Newton方法
fprintf('\n')
fprintf('对偶Newton方法:\n')
figure(3)
[ figure3,calTime3]=Func3(zeros(p,1),MaxIter,yita,alpha,beta,A,b,'bo-');
title('对偶Newton方法');
hold on
4 运行结果
4.1 标准牛顿方法

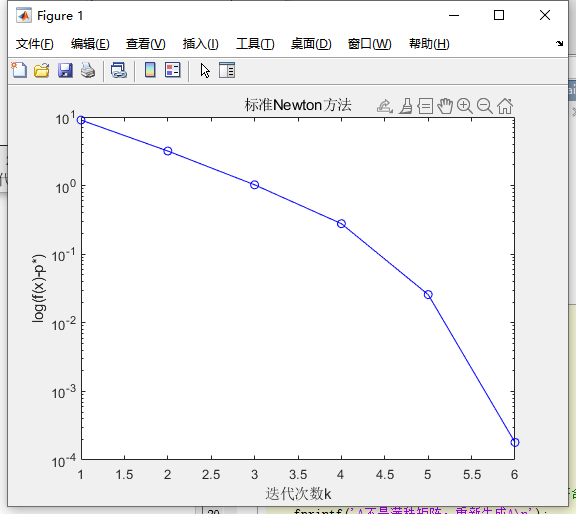
4.2 不可行初始点Newton方法

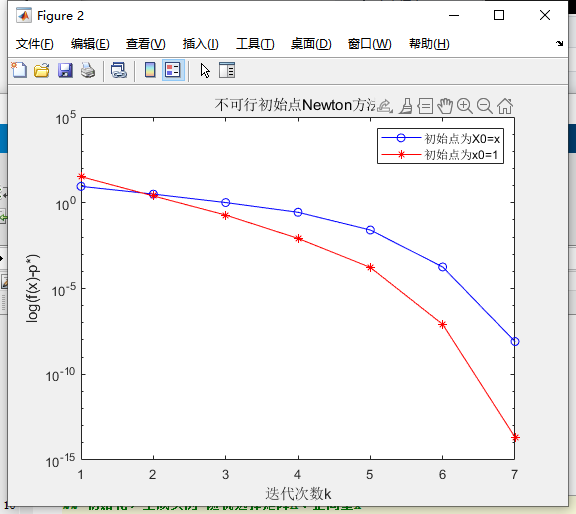
4.3 对偶牛顿方法

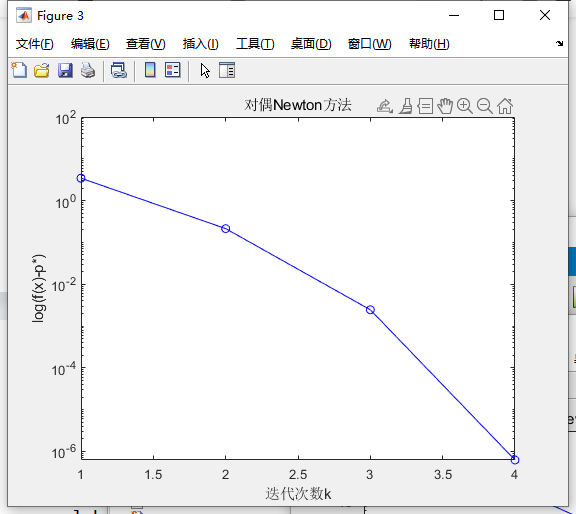
综上,证明了三种方法求得的最优结果相同
且一般有迭代次数:对偶<标准<不可行



