西安交通大学 优化方法 大作业1 无约束优化问题

写在最前面：如果你还没有在选课端选择这门课或是选课端还在开放时间段，强烈建议退选优化方法并换选数学建模

\(对于{R^2}空间非二次规划问题min f(x)= e ^ {x_{1}+3x_{2}-0.1} + e^{x_{1}-3x_{2}-0.1}+ e^{-x_{1}-0.1}，分析回溯直线搜索采用不同的\alpha，\beta值时，误差随迭代次数改变的情况。注：初始值相同\)

分析
目标函数：
\(min f(x)= e ^ {x_{1}+3x_{2}-0.1} + e^{x_{1}-3x_{2}-0.1} + e^{-x_{1}-0.1}\)
采用梯度下降法确定下降方向d
采用回溯直线搜索确定步长t
\(x_{1}=x_{2}=0\)

import pandas as pd
import numpy as np
from matplotlib.pyplot import figure,plot,show,xlabel,ylabel,legend
from math import exp

def f(x1,x2):
        "最优化的目标函数"
        return exp(x1+3*x2-0.1)+exp(x1-3*x2-0.1)+exp(-x1-0.1)

def f_grad(x1,x2):
        "目标函数梯度"
        return [exp(x1+3*x2-0.1)+exp(x1-3*x2-0.1)-exp(-x1-0.1),3*exp(x1+3*x2-0.1)-3*exp(x1-3*x2-0.1)]

def grad_descent(alpha, beta):##输入参数α、β
    "采用梯度下降法确定d"
    x1 = x2 = 0
    y = f(x1,x2)
    maxIter = 300##最大迭代次数

    err = 1.0
    curve2 = [y]
    it = 0
    gradient=f_grad(x1,x2)

    while (gradient[0] ** 2 + gradient[1] **2 > 1e-10) and it < maxIter:
        it += 1
        gradient = f_grad(x1,x2)
        
        "回溯直线搜索"
        step = 1.0
        while f(x1 - step * gradient[0], x2 - step * gradient[1]) > y - alpha * step * (gradient[0] ** 2 + gradient[1] ** 2):
            step *= beta
        x1 = x1 - step * gradient[0]
        x2 = x2 - step * gradient[1]
        new_y = f(x1, x2)
        err = y - new_y##偏差
        y = new_y
        
        curve2.append(y)
    for i in range(len(curve2)):
        curve2[i]-=y
    return curve2,y,it##最终得到当前α、β对应的曲线

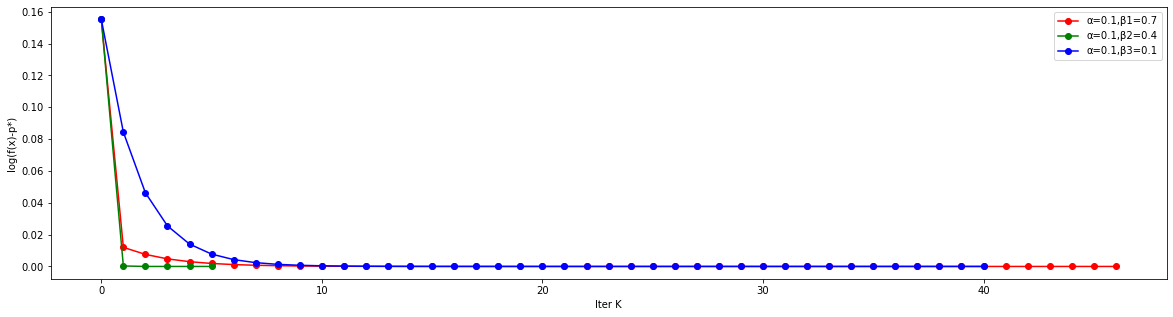
取相同的\(\alpha=0.1\)，三种不同的\(\beta\)
其中，\(\beta_1=0.7,\beta_2=0.4,\beta_3=0.1\)

figure(figsize=(20,5))
curve1, y1, k1=grad_descent(0.1,0.7)
curve2, y2, k2=grad_descent(0.1,0.4)
curve3, y3, k3=grad_descent(0.1,0.1)
plot(curve1,'ro-')
plot(curve2,'go-')
plot(curve3,'bo-')
xlabel("Iter K")
ylabel("log(f(x)-p*)")
legend(['α=0.1,β1=0.7','α=0.1,β2=0.4','α=0.1,β3=0.1'])
show

print("β1，β2，β3对应的最优值分别是：")
print(y1)
print(y2)
print(y3)
print("β1，β2，β3对应的迭代次数分别是：")
print(k1)
print(k2)
print(k3)

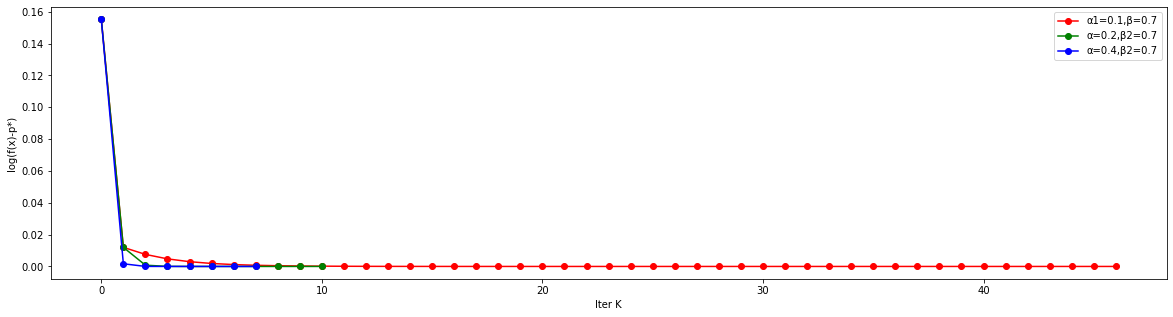
figure(figsize=(20,5))
curve1, y1, k1=grad_descent(0.1,0.7)
curve2, y2, k2=grad_descent(0.2,0.7)
curve3, y3, k3=grad_descent(0.4,0.7)
plot(curve1,'ro-')
plot(curve2,'go-')
plot(curve3,'bo-')
xlabel("Iter K")
ylabel("log(f(x)-p*)")
legend(['α1=0.1,β=0.7','α=0.2,β2=0.7','α=0.4,β2=0.7'])
show

print("α1，α2，α3对应的最优值分别是：")
print(y1)
print(y2)
print(y3)
print("α1，α2，α3对应的迭代次数分别是：")
print(k1)
print(k2)
print(k3)