二分查找法

https://www.zhihu.com/search?q=%E4%BA%8C%E5%88%86%E6%9F%A5%E6%89%BE&utm_content=search_history&type=content

C++ <algorithm>的四个二分查找函数：搜索区间为[first, last)，左闭右开区间

1.lower_bound(val) 返回第一个不小于val的位置，若不存在，返回last

2.upper_bound(val) 返回第一个大于val的位置，若不存在，返回last

3.equal_range(val) 返回[lower_bound(val), upper_bound(val)]

4.binary_search(val) 在搜索区间内是否有元素==val（其实是调用lower_bound来判断）

 

二分查找法可以分为求上下界两种：

1.求下界，即找满足 x>= val 或 x > val 条件的最小x的位置，分别对应lower_bound 和 upper_bound

2.求上界，即找满足x < val 或 x <= val 条件的最大x的位置，可以调用互补的求下界的函数再减一得到，如 x >= val 的下界再减一就是x < val的上界，x > val 的下界再减一就是x <= val 的上界

 

int lowerBound(vector<int>& arr, int l, int r, int val){
    while(l < r){
        int m = l + (r - l) / 2;
        if(arr[m] < val) l = m + 1;
        else r = m;
    }
    return l;
}

int upperBound(vector<int>& arr, int l, int r, int val){
    while(l < r){
        int m = l + (r - l) / 2;
        if(arr[m] <= val) l = m + 1;
        else r = m;
    }
    return l;
}

 

Leetcode33. Search in Rotated Array

 

 

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int n = nums.size();
        int l = 0, r = n - 1;
        while(l < r){
            int m = l + (r - l) / 2;
            if(nums[m] > nums[r]) l = m + 1;
            else r = m;
        }
        int rot = l;
        l = 0, r = n - 1;
        while(l <= r){
            int m = l + (r - l) / 2;
            int realmid = (m + rot) % n;
            if(nums[realmid] == target) return realmid;
            else if(nums[realmid] < target) l = m + 1;
            else r = m - 1;
        }
        return -1;
    }
}

  mid 把区间分为两半，其中一半必然有序，另一半还是rotated，根据 target 是否在有序的那一半中，就可以更新 left 或 right 了。

public:
    int search(vector<int>& nums, int target) {
        int n = nums.size();
        int l = 0, r = n - 1, mid;
        while (l <= r) {
            mid = l + ((r - l) >> 1);
            if (nums[mid] == target) return mid;
            if (nums[mid] >= nums[l]) {
                if (target < nums[mid] && target >= nums[l]) {
                    r = mid - 1;
                }
                else {
                    l = mid + 1;
                }
            }
            else {
                if (target >nums[mid] && target <= nums[r]) {
                    l = mid + 1;
                }
                else {
                    r = mid - 1;
                }
            }
        }
        return -1;
    }
};

 

Leetcode81. Search in Rotated Sorted Array II

 

 

 

 

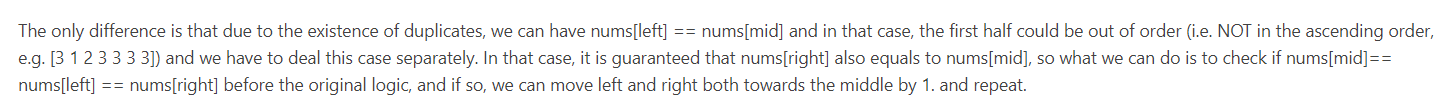
//方法1
class Solution {
public:
    bool search(vector<int>& nums, int target) {
        int l = 0, r = nums.size() - 1, m;
        while(l <= r){
            m = l + (r - l) / 2;
            if(nums[m] == target) return true;
            if((nums[l] == nums[m]) && (nums[m] == nums[r])) {
                ++l;--r;
            }
            else if(nums[l] <= nums[m]){
                if((nums[l] <= target) && (nums[m] > target)) r = m - 1;
                else l = m + 1;
            }
            else{
                if((nums[m] < target) && (nums[r] >= target)) l = m + 1;
                else r = m - 1;
            }
        }
        return false;
    }
};

//方法2：先二分查找pivot，再二分查找target
class Solution {
public:
    bool search(vector<int>& nums, int target) {
        int n = nums.size();
        int l = 0, r = n - 1;
        while(l < r){
            int m = l + (r - l) / 2;
            if(nums[m] > nums[r]) l = m + 1;
            else if(nums[m] < nums[r]) r = m;
            else{
                if(nums[r - 1] > nums[r]){
                    l = r;
                    break;
                }
                r--;
            }
        }
        int pivot = l;
        cout << pivot;
        l = 0, r = n;
        while(l < r){
            int m = l + (r - l) / 2;
            int realmid = (m + pivot) % n;
            if(nums[realmid] < target) l = m + 1;
            else r = m;
        }
        return l != n && nums[(l + pivot) % n] == target;
    }
};

 

 

 Leetcode153. Find Minimum in Rotated Sorted Array

 

 

 

class Solution {
public:
    int findMin(vector<int>& nums) {
        int n = nums.size();
        int l = 0, r = n - 1, m;
        while(l < r){
            m = l + (r - l) / 2;
            if(nums[m] > nums[r]) l = m + 1;
            else r = m;
        }
        return nums[l];
    }
};

 

Leetcode154. Find Minimum in Rotated Array II

 

 

class Solution {
public:
    int findMin(vector<int>& nums) {
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int m = l + (r - l) / 2;
            if(nums[m] > nums[r]) l = m + 1;
            else if(nums[m] < nums[r]) r = m;
            else{
                if(nums[r - 1] > nums[r]){
                    l = r;
                    break;
                }
                r--;
            };
        };
        return nums[l];
    }
};

 

Leetcode34. Find First and Last Position of Element in Sorted Array

 

 

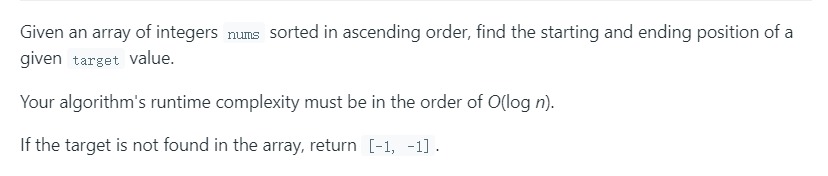
class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int l = lowerBound(nums, 0, nums.size(), target);
        int r = lowerBound(nums, 0, nums.size(), target + 1);
        if(l == nums.size() || nums[l] != target) return {-1, -1};
        else return {l, r - 1};
    }
    
    int lowerBound(vector<int>& arr, int l, int r, int target){
        while(l < r){
            int m = l + (r - l) / 2;
            if(arr[m] < target) l = m + 1;
            else r = m;
        }
        return l;
    }
    
};

 

Leetcode69. Sqrt(x)

 

 

class Solution {
public:
    int mySqrt(int x) {
        if(x == 1) return 1; //寻找num * num <= x的num的最大值，相当于找x的upperbound
        int l = 1, r = x;
        while(l < r){
            int m = l + (r - l) / 2;
            if(m <= x / m) l = m + 1;
            else r = m;
        }
        return l - 1;
    }
};