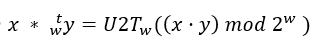2018-2019-1 20165330 《信息安全系统设计基础》第二周学习总结
学习内容总结
信息的表示与处理
- 字节:计算机中最小的可寻址的内存单元
- 虚拟内存:机器级程序将内存视为一个非常大的字节数组
- 进制表示及转换
- 十进制:D=dndn-1...d1d0.d-1...d-m(m,n为正整数)
- 二进制:B=bnbn-1...b1b0.b-1...b-m(m,n为正整数)
- 八进制:O=onon-1...o1o0.o-1...0-m(m,n为正整数)
- 十六进制:H=hnhn-1...h1h0.h-1...h-m(m,n为正整数),在C语言中以0x或0X开头的数字常量为十六进制的值
- 进制转换:
- 十进制转换R进制:整数部分除以R,商为权值,直至商为0并以下至上排列;小数部分不断乘R记录结果的整数部分并以上至下排列
- 二进制转换八进制:每三位为一个八进制,不足在最高位补0
- 二进制转换十六进制:每四位为一个十六进制,不足在最高位补0
- 对于一个字长为w位的机器,虚拟地址的范围为0~2w-1,程序最多访问2w个字节
- 可在32位或64位机器上运行的程序指令:
gcc -m32 prog.c - 大端法规则:最高有效字节在最前面
- 小端法规则:最低有效字节在最前面
- 在计算机系统中,程序仅仅只是字节序列
- 位级运算
- 位向量:固定长度为w、由0和1组成的串,绝大多数可表示一个数
- 位级运算包括:
- “|”或运算:两个0时为0
- “&”与运算:有0即为0
- “~”非运算:即取反
- “^”异或运算:两个相同数为0
- 逻辑运算
- 在逻辑运算中,只有0、1两种表示,非零参数都表示TRUE,0表示FALSE
- 逻辑运算包括:
- “&&”:与1与为true,与0与为false
- “||”:有操作数为true则为true
- “!”:取反
- 移位运算
- 左移x<<k:左移k位,最右边补k个0
- 算术右移x>>k:右移k位并在最左端补k个最高有效位上的值
- 逻辑右移x>>>k:右移k位,最左边补k个0
- 对有符号数采用算术右移,对无符号数采用逻辑右移
整数表示
- 信息=位+上下文
- 无符号整数:B2U4[0011]=0·23+0·22+1·21+1·20=3
- 有符号整数-补码编码:B2T4[1011]=-1·23+0·22+1·21+1·20=-5
- 无符号数表示需加后缀字符u
- 浮点数
- 二进制小数
- IEEE浮点表示
- 表示:
V=(-1)^sM2^E - 符号s决定着这个数是负数(s=1)还是正数(s=0)
- 尾数 M是一个二进制小数,n位小数字段f=fn-1…f1f0编码尾数M
- 阶码 E的作用是对浮点数加权,这个权重是2^E,e=ek-1…e1e0
- 偏移常数
Bias = {2^k}{^-}{^1}-1 - 32位浮点数:

- 规格化的值
- E=e-Bias M=1+f
- 非规格化的值
- E=1-Bias M=f
- 表示:
数值运算
- 无符号整数
- 加法
- 当发生溢出情况时,丢弃所溢出的最高位,所得到的结果是
x + y (mod 2^w) - 公式
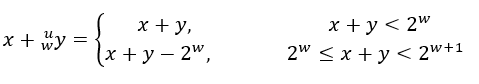
- 当发生溢出情况时,丢弃所溢出的最高位,所得到的结果是
- 乘法
- 公式:
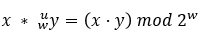
- 在大多数机器上,整数乘法指令相当慢,常采用用移位和加法运算的组合来代替乘法运算
- 公式:
- 除法:向下取整
- x/2 实际上是x的位向量向右移1位
- x/16 是x向右移4位
- 加法
- 补码运算
- 加法
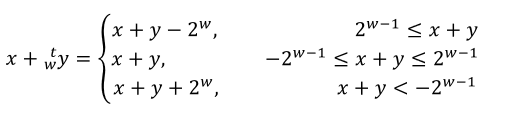
- 乘法
- 除法:算术右移
- 加法
信息的存储
- 网络字节序
- 网络上的数据流是字节流,收到的第一个字节被当作高位看待
- 网络字节序是大端字节序
- 主机字节序和网络字节序转换
- htons()把unsigned short类型从主机序转换到网络序
- htonl() 把unsigned long类型从主机序转换到网络序
- ntohs() 把unsigned short类型从网络序转换到主机序
- ntohl() 把unsigned long类型从网络序转换到主机序
其中 网络net即n 主机host即h long(32位)即l short(16位)即s
课下作业
完成教材 p97 2.96 2.97,要有完备的测试
2.96
- 任务详情
- 遵循位级浮点编码规则,实现具有如下原型的函数:
/*
*Compute (int) f.
*If conversion causes overflow or f is NaN, return
*/
int float_f2i(float bits f);
- 对于浮点数f,这个函数计算(int)f。如果f是NaN,你的函数应该向零舍人。如果f不能用整数表示(例如,超出表示范围,或者它是一个NaN),那么函数应该返回0x800000000。
- 测试你的函数,对参数f可以取的所有2^32个值求值,将结果与你使用机器的浮点运算得到的结果相比较。
- 分析
NaN: not a number,表示“无效数字”。- 首先,看是否是浮点数且不超范围,超过表示范围,置为最大整数,若太小,不能化为整数,置为0。其次看符号 设置+,-号。如果是NaN,置为0x80000000
- 函数形参为无符号型,输入负数时和整数转化不同,加了一行代码打印当前输入,负数时,将无符号转化为浮点型解决
- 代码
#include <stdio.h>
#include <math.h>
typedef float float_bits;
int float_f2i(float_bits f)
{
printf("your num is %f\n",f);
if(f>=0&&f<=32767)
return fabs(f);
else if(f<0&&fabs(f)<32768)
return -fabs(f);
else
return 0x80000000;
}
int main(){
float_bits i;
scanf("%f",&i);
printf("float_f2i is %d,(int) is %d\n",float_f2i(i),(int)i);
return 0;
}
- 运行截图
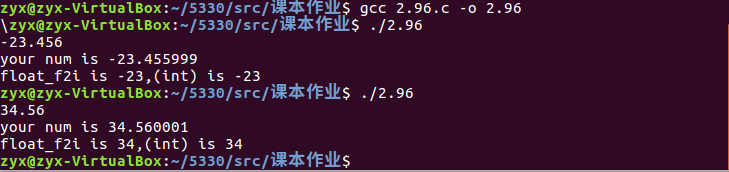
2.97
- 任务详情
- 遵循位级浮点编码规则,实现具有如下原型的函数:
/*Compute (float) i*/
float bits float_i2f(int i);
- 对于函数i,这个函数计算(float) i的位级表示。
- 测试你的函数,对参数f可以取的所有2^32个值求值,将结果与你使用机器的浮点运算得到的结果相比较。
- 代码
#include <stdio.h>
#include <limits.h>
typedef unsigned float_bits;
float_bits float_i2f(int i)
{
unsigned u = (unsigned)i;
if(!u)
return 0u;
unsigned sign = u>>31;
unsigned exp,frac,f;
if(sign)
u=(~u)+1;
unsigned j,leftmost_one;
for(j=0;j<32;j++)
{
leftmost_one=u&(0x80000000>>j);
if(leftmost_one)
break;
}
exp = 158u-j;
f = u<<j<<1;
unsigned last_bit=(f&0x200)>>9;
unsigned truncation = f&0x1ff;
if(truncation<0x100)
frac = f>> 9;
else if(truncation >0x100)
frac= (f>>9)+1;
else
{
if(last_bit)
frac = (f>>9)+1;
else
frac = f>>9;
}
if(frac >>23)
{
++exp;
frac=0;
}
return (sign<<31)|(exp<<23)|frac;
}
int main()
{
int i;
unsigned r;
float f,fr;
for(i=INT_MIN;i<=INT_MAX;i++)
{
r=float_i2f(i);
fr=*((float*)&r);
f=(float)i;
if(fr == f)
printf("%d:ok\n",i);
else
{
printf("%d: %f %f error\n",i,f,fr);
return -1;
}
}
}
- 运行截图