请输入标题
\[\def\d{\mathrm{d}}
\def\i{\mathrm{i}}
\def\e{\mathrm{e}}
\newcommand{\pian}[2]{\dfrac{\partial {#1}}{\partial {#2}}}
\def\re{\mathrm{Re}}
\def\Im{\mathrm{Im}}
\]
配一下 Gedit 的一键编译
sudo apt-get install gedit-plugins
#!/bin/sh
fullname=$GEDIT_CURRENT_DOCUMENT_NAME
dir=$GEDIT_CURRENT_DOCUMENT_DIR
name=${fullname%.*}
g++ $fullname -o $name -g -Wall -std=c++11
if test $? -eq 0; then
echo "Compile Success."
gnome-terminal -- bash -c "
time $dir/$name
echo
read
"
else
echo "Compile Failed."
fi
#!/bin/sh
fullname=$GEDIT_CURRENT_DOCUMENT_NAME
dir=$GEDIT_CURRENT_DOCUMENT_DIR
name=${fullname%.*}
gnome-terminal -- bash -c "gdb $dir/$name"
6.3 一个曲线积分
计算以下第一类曲线积分的值 \((a^2+b^2 \neq r^2)\),
\[\oint_{C_r} \ln \sqrt{(x-a)^2+(y-b)^2} \d{s} \]
Proof / 设 \(z_0=a+b\i,z=r\e^{\i \theta} \in C_r \subset \mathbb{C}\).
则 \(\d{z}=\i r \e^{\i \theta}\d{\theta} \implies \d{s}=r\d{\theta}=\dfrac{r\d{z}}{\i z}\).
把第一类曲线积分写成复积分,从而有
\[\begin{aligned}
I&=\int_{C_r} \log|z-z_0| \d{s} \\
&=\int_{C_r} \re(\log(z-z_0)) \d{s} \\
&=\re\left(\dfrac{r}{\i}\int_{C_r}\dfrac{\log(z-z_0)}{z}\d{z} \right) \\
&= r \cdot\Im \left(\int_{C_r}\dfrac{\log(z-z_0)}{z}\d{z} \right)
\end{aligned}
\]
-
若 \(|z_0| > r\),则在 \(C_r\) 及其内部只有 \(z=0\) 一个奇点,直接由留数定理,
\[\int_{C_r}\dfrac{\log(z-z_0)}{z}\d{z}=2\pi\i \log(-z_0) \]\[I=2\pi r\cdot\re(\log (-z_0))=2\pi r\ln|z_0| \] -
若 \(|z_0| <r\),则在 \(C_r\) 内部 \(\log(z-z_0)\) 有瑕线,用如下围道绕过这些部分:
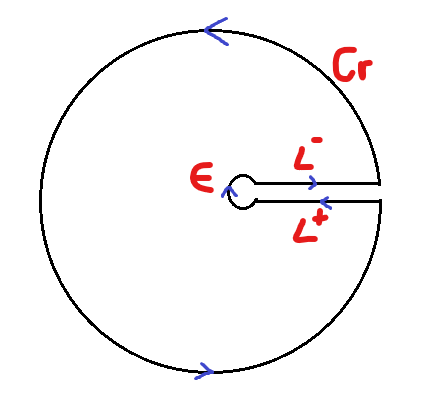
设整个围道作 \(\Gamma\), 由(1)知
\[\oint_\Gamma f(z)\d{z}=2\pi \i \log(-z_0) \]不妨设 \(p=|z_0|\),且瑕点即为 \(p\),首先
\[\epsilon \to 0,\int_{p(\epsilon)}f(z)\d{z}=0, \]而当 \(\epsilon \to 0\) 时,根据复对数函数的定义,
\[\int_{L^+}f(z)\d{z} = \int_r^p \dfrac{\ln(x-p)+2\pi \i}{x}\d{x}, \\ \int_{L^-} f(z)\d{z}=\int_p^r \dfrac{\ln(x-p)+0 \i}{x} \d{x}, \]所以,
\[\left(\int_{L^+}+\int_{L^-}\right) f(z)\d{z}=2\pi \i \ln(\dfrac p r) \]根据四条路径的求和
\[\left(\int_{C_r}+\int_{L^+}+\int_{p(\epsilon)}+\int_{L^-}\right) f(z)\d{z}=\int_\Gamma f(z)\d{z} \]故可得
\[\int_{C_r} f(z)\d{z}=2\pi \i \left(\ln(\dfrac p r) - \log (-z_0)\right) \]所以这种情况下,
\[I= r \cdot \Im \left( \int_{C_r} f(z)\d{z} \right) = 2\pi r \ln r \]
综上所述
\[I=\begin{cases}
2\pi r \ln \sqrt{a^2+b^2} & (a^2+b^2>r^2) \\
2\pi r\ln r & (a^2+b^2<r^2)
\end{cases}
\]

