近日模考理数压轴题简记
参加了几次联考,数学无一例外的垫底了。
A.皖南八校第二次联考·解析几何
21、抛物线 \(y^2=4x\),焦点 \(F(1, 0)\);过外一点 \(A\) 引切线 \(AB, AC\) ,令 \(M\) 为 \(\triangle ABC\) 的外心。(2)求 \(\sin AFM\) 的值域。
考场做了半小时。自闭了。听说很多巨佬考场切了此题。
第一步可能要先画个图,猜出来角度一定是 \(90\) 度(然而我当时画的图量出来二三十度……);;
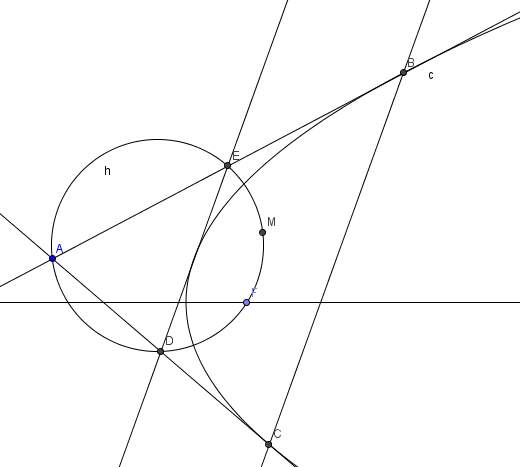
证明的话,可以考虑一堆熟知结论的堆砌:
比如你作出中位线 \(DE\),容易得到直线 \(DE\) 是抛物线的切线(用相关点法算下 \(DE\) 的方程即可);
根据外心即 \(ME⊥AB\),\(MD⊥AC\),那么 \(ADEM\) 四点共圆,且 \(AM\) 为直径;
注意到 \(ADE\) 来自三条切线构成的三角形,根据江西第一次质检的解析几何题,容易得到 \(F\) 在 \(ADE\) 的外接圆上;
那么 \(A,D,E,M,F\) 五点共圆,而 \(AM\) 是直径,即证 \(\angle AMF = 90°\)。
B.江淮十校第二次联考·导数
21、(2)\(f(x)=mx-\ln x\) 有两零点 \(x_1, x_2\) ,求证: \(x_1+x_2 > {3\over m} - e\)
这个题看到之后发现是某个老题的变形,然后现场过了。另外也没人考场切了此题。
从这篇 2018 年的文章来看,既然是拿两年前的老题改的,那么大家都有经验也不奇怪。
我们考虑这个题的函数可以变形为 \(g(x)={\ln x \over x} - m\) ,那么它的极值点为 \(e\);
那么只需把 \({e\over x_1}\) 、 \({x_2\over e}\) 代入常用对数不等式 \(\ln x > {2(x-1)\over x+1}\) 化简即证。
另外,如果我们考虑原函数的极值点呢? 那么可以证得 : \(x_1 + x_2 > {1-\ln m \over m}\)。
upd at May:近来考的安徽六校和江南十校联考,数学科目都比较简单,就不写了。
C.芜湖二模·导数
题意:\(f(x)=\tan x-\dfrac 1 3 a x^3-x\) 在 \((0,\dfrac \pi 2)\) 上恒正 ,求 \(a\) 的取值范围。
那么看到这个题很容易直接考虑端点效应,但实际操作难度不亚于【2018·全国III卷】:
【2018·全国III卷】已知函数f(x)=(2+x+ax²)ln(1+x) - 2x.
(1)若a=0,证明:当-1﹤x﹤0时,f(x)﹤0;当x﹥0时,f(x)﹥0;
(2)若x=0是f(x)的最大值点,求a。
由于我在考场上采用了上述方法,考虑到完整性很难避免四次连续求导过程,因此答题卡空间大小成为了一个较大的障碍。我们考后亦猜测作者有意图之。
就模考这道题,标答采取的策略比较小巧:$$f'(x)=\sec ^2 x -ax^2-1=\tan ^2 x -ax^2$$ 那么当 \(a>0\) 时 $$f'(x)=(\tan x -\sqrt a x)(\tan x + \sqrt a x)$$
至此很容易即得到 \(a\le 1\),套用二阶端点效应就可以在格子里面写完整道题了!
D.江南十校考试后某次模拟题·三角函数
18.在 \(\triangle ABC\) 中,内角 \(A,B,C\) 对的边分别为 \(a,b,c\)。\(A,B\) 均为锐角,\(a\sin A+b\sin B=c=1\)。
(1)直接写出 \(\angle C\) 的大小。
(2)是否存在一个满足上述条件的 \(\triangle ABC\) ,使得 \(\sin(a)=\cos(b)\)?请说明理由。
第一问还是很有意思的!小题狂练上有一道一样的选择题。当然还是比较容易得到 \(C=\frac \pi 2\) 的。
第二问相当于问 \(\sin \sin x = \cos \cos x\) 是否有解!这个其实在实数集上都是无解的!在 \((0,\frac \pi 2)\) 上,只需要利用有界性即可!
E.江南十校考试后某次模拟题·立体几何
19.如图,\(AD\) 与 \(BC\) 是四面体 \(ABCD\) 中互相垂直的棱,\(|BC|=2\),若 \(|AD|=2c\),且 \(|AB|+|BD|=|AC|+|CD|=2a\),其中 \(a\)、\(c\) 为常数。
(1)求证:\(|AB|=|AC|\)。
(2)若 \(a=10,c=7\),当四面体 \(ABCD\) 体积最大时,求直线 \(AD\) 与平面 \(ABC\) 夹角的正弦值。
这道题的原题来自 高考真题。
因此只要将体积函数化,很容易推出体积最大的位置是中间位置,再结合几何法就很容易计算答案了!
F.安徽六校第二次联考·解析几何
20.题面略。出题人裸搬 知乎 上的问题。
不得不推荐此题,因为还蛮有意思的。这道题直接采取知乎回答中的方法算即可,整体来说计算量不小。反正我考场过了(((
ps:安徽六校联考好几次考了蒙日圆的问题
G.安师大附中最后一模·导数
21.(1)略,大概是给了一个很松的放缩
(2)求证:\(\displaystyle \sum_{i=1}^n \sin \frac{1}{i^2+1} \lt \frac 1 2 + \ln 2\)。
在考场上发现第一问给的放缩太松了,肯定打不过 \(\sin x < x\) 的精度!
于是乎只需证 \(\displaystyle \sum_{i=1}^n \frac{1}{i^2+1} \lt \frac 1 2 + \ln 2\);
这个式子是不可算的,但 \(\sum \dfrac 1 {n^2}\) 是可算的!所以我们根据 \(\sum \dfrac 1 {n^2}=\dfrac {\pi^2}{6}\) 的推论,可以考虑考虑把前面的按住不动,后面的直接按巴塞尔问题解决。
那么其实按住第一项就能过了,因而 \(\displaystyle \sum_{i=2}^n \frac{1}{i^2+1} \lt \sum_{i=2}^n \frac{1}{i^2} \lt \sum_{i=2}^n \frac{1}{i^2-\frac 1 4}\),这个可以裂项即 \(\dfrac{1}{n^2-\frac 1 4}=\dfrac{1}{n-\frac 1 2}-\dfrac{1}{n+\frac 1 2}\),因此 \(\sum_{i=2}^n \frac{1}{i^2-\frac 1 4} \lt \frac 2 3 \lt \ln 2\),也就是说证明了给定命题的加强。
如果固定前两项,可以说:\(\displaystyle \sum_{i=1}^n \sin \frac{1}{i^2+1} \lt 1.1\)。
H.2021高考全国乙卷(安徽高考)·选择题第十二题
12.比大小:\(a=2\ln 1.01,b=\ln 1.02,c=\sqrt{1.04}-1\)。
根据麦克劳林级数展开 \(\ln(1+x)=x-\dfrac{x^2}{2}+\dfrac{x^3}{3} \dots\),\(\sqrt{1+x}=1+\dfrac{x}{2}-\dfrac{x^2}{8}+\dfrac{x^3}{16} \dots\),注意到 \(x\) 的精度高达 \(ε = 10^{-2}\) 其实不会对后面的位造成影响,那么直接比较级数式即可。
于是可设 \(t=10^{-2}\),代入级数立刻得 \(b<c<a\)。
但此题中 \(b<a\) 是显然的,要计算 \(a,c\) 大小关系,直接以手动开根号方法算出 \(c\) 也是可行的。由上述级数比较可知需要保留六位左右的精度。
I.太高妙了·构造
求证:集合 \(\{2,3,4,\dots,3n+1\}\) 可以划分为 \(n\) 个三元组,且每个三元组均为钝角三角形的三边长。
J.2021新高考全国I卷·导数
21.(1)略
(2)设 \(f(x)=x(1-\ln x)\),\(f(x)=m\) 有两解 \(a,b\) 求证:\(2<a+b<\mathrm{e}\)。
解:右边是极值点偏移。左边同哈尔滨三中三模导数压轴题按对称化构造的待证式子(那道题最后一问出题人觉得太难了答案略去了)。
这道题太原题了。

