prim算法 poj1258 Agri-Net 最小生成树基础题
Agri-Net
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 64460 | Accepted: 26642 |
Description
Farmer John has been elected mayor of his town! One of his campaign promises was to bring internet connectivity to all farms in the area. He needs your help, of course.
Farmer John ordered a high speed connection for his farm and is going to share his connectivity with the other farmers. To minimize cost, he wants to lay the minimum amount of optical fiber to connect his farm to all the other farms.
Given a list of how much fiber it takes to connect each pair of farms, you must find the minimum amount of fiber needed to connect them all together. Each farm must connect to some other farm such that a packet can flow from any one farm to any other farm.
The distance between any two farms will not exceed 100,000.
Farmer John ordered a high speed connection for his farm and is going to share his connectivity with the other farmers. To minimize cost, he wants to lay the minimum amount of optical fiber to connect his farm to all the other farms.
Given a list of how much fiber it takes to connect each pair of farms, you must find the minimum amount of fiber needed to connect them all together. Each farm must connect to some other farm such that a packet can flow from any one farm to any other farm.
The distance between any two farms will not exceed 100,000.
Input
The input includes several cases. For each case, the first line contains the number of farms, N (3 <= N <= 100). The following lines contain the N x N conectivity matrix, where each element shows the distance from on farm to another. Logically, they are N lines of N space-separated integers. Physically, they are limited in length to 80 characters, so some lines continue onto others. Of course, the diagonal will be 0, since the distance from farm i to itself is not interesting for this problem.
Output
For each case, output a single integer length that is the sum of the minimum length of fiber required to connect the entire set of farms.
Sample Input
4 0 4 9 21 4 0 8 17 9 8 0 16 21 17 16 0
Sample Output
28
Source
最后有图解
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#define maxn 500
#define INF 0x3f3f3f3f ///无穷大
#define mem(a,b) memset(a,0,sizeof(a))
#define min(a,b) (a>b?b:a)
using namespace std;
//poj 1258
int map[maxn][maxn]; ///存图,map[i][j] = q表示从点i到j的距离为q
bool Is_Used[maxn]; ///Is_Used[i] = true表示点i已经在最小生成树中
int Low_Cost[maxn]; ///Low_Cost[i] 表示最小生成树中所有点到i点的最小值
int n; /// 图大小
void prim() {
int ans = 0;
mem(Is_Used,0); ///将Is_Used数组清0
Is_Used[0] = true; ///将V0存入树中做起点
for(int i=1; i<n; i++)///因为树中只有V0,所以到每个点的最小距离为V0到每个点的距离,即map[0][i]
Low_Cost[i] = map[0][i];//初始化
for(int i=1; i<n; i++) {///此循环为遍历没有在树中的点
int Min = INF;
int New_Point = -1; ///新点坐标存为-1表示不存在
for(int j=0; j<n; j++) { ///找到在树中的点到不在树中的点的最小的距离,存为新的点
if(!Is_Used[j] && Min > Low_Cost[j]) {
Min = Low_Cost[j];
New_Point = j;
}
}
ans += Min;
Is_Used[New_Point] = true;///将新加入的点标记为已在树中
for(int j=0; j<n; j++)
if(!Is_Used[j]) ///更新最小花费的数组,使得循环完了之后树中的点到每一个没在树中的点都是最小距离
Low_Cost[j] = min(Low_Cost[j],map[New_Point][j]);
} ///循环完,证明所有点已经在树中还需要循环i:0->n 判断所有Is_Used[i]是不是已经使用,不过这道题用不上
printf("%d\n",ans);
}
int main() {
int i,j;
while(scanf("%d",&n)!=EOF&&n) {
for(i=0; i<n; i++)
for(j=0; j<n; j++)
scanf("%d",&map[i][j]); //输入边的信息
prim();
}
return 0;
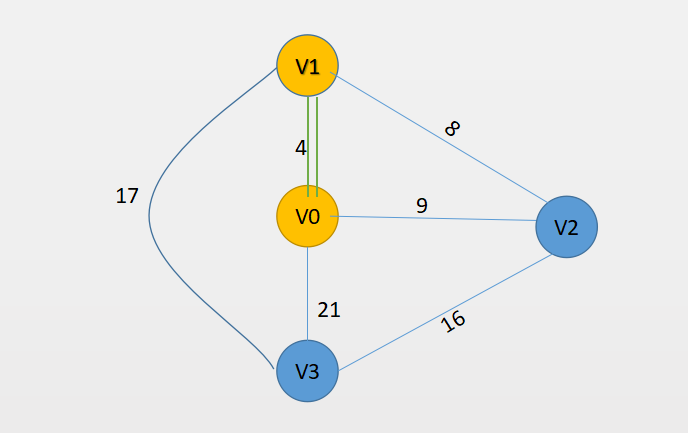
}第一步我们把V0加入生成树中,然后把Low_Cost更新
此时的Low_Cost = [4,9,21] (Low_Cost[V0]虽然在里面但是不会使用,因为已经在树中了,下面同理)
然后我们找Low_Cost里面最小的,就是map[V0][V1],为4,那么好,把V1加入树中,更新Low_Cost
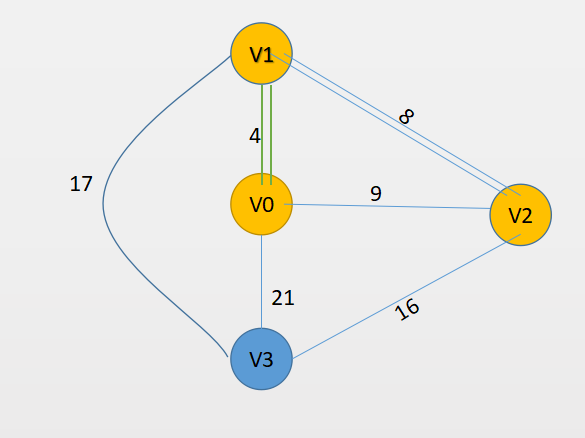
///双线表示已经连接在树里面的点
此时Low_Cost就是V1和V0到V2和V3的公共最短边了
更新后为Low_Cost[] = [8,17]
然后涂黄距离最小的V2
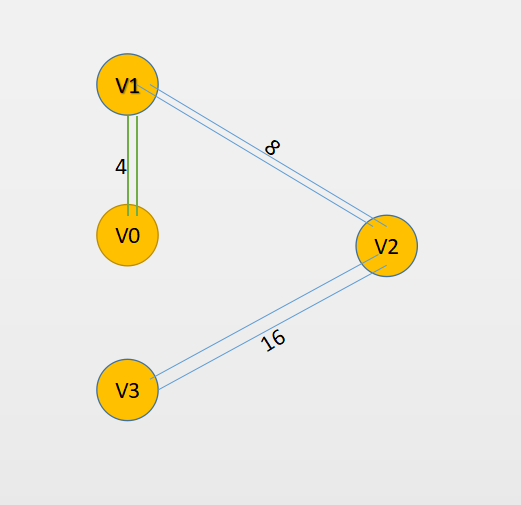
Low_Cost里面只剩下16了,继续加入
所以ans = 4 + 8 + 16 = 28
最后的树长这样
有不懂的地方欢迎留言
博主也是刚刚理解prim算法
如果讲错的欢迎指正~~~



 浙公网安备 33010602011771号
浙公网安备 33010602011771号