KMP算法详解及模板
KMP是一个用于字符串匹配的算法,用于求解串str2是否在串str1中出现并返回出现的位置(str1的长度>=str2的长度)
由于<cstring>里内置的子串查找函数时间复杂度太高(BF算法时间复杂度O(n*m)),所以数据过大时得手写kmp(O(n+m))
先理清楚2个概念
1.前缀和后缀
这是百度百科的解释
汉语里指在词根前面的构词成分。如“阿哥”、“阿姨”中的“阿”,英文中指一个英语单词可以分为三个部分:前缀(prefix),词根(stem)及后缀(suffix)。单词中位于词根前面的部分就是前缀。前缀,可以改变单词的意思。
引申到串里,如果串的长度为leng ,那这个串的前缀就可以是从str[0]到str[leng-1]中的任何一组
比如说一个串abcdef 那么它的前缀和后缀可以是下面几种情况
前缀 后缀
abcde bcdef
abcd cdef
abc def
ab ef
a f
2.next数组
这个数组是用来记录str2各个位置与str2其他位置的匹配信息的
比如说一个串str2 = "abcdabce",str1 = "abcdabcd******"
如果我们在和str1匹配的过程中已经确定匹配了"abcdabc"
然后只需要确定str1的下一个字符是"e"就能确定str2在str1中出现过了
但是现实总是骨感的,偏偏str1下一个字符是' d',匹配失败
传统的算法是又从str1第二个字符'b'开始,str2从str2第一个字符'a'开始匹配.这样时间就花费的很多,因为我们可以直接看出来,匹配失败后,str1可以从第一个'*'开始,str2可以从第二个'a'(str2[4])开始"再续前缘" ,而所谓的next就是储存这个"再续前缘"的位置信息的,因为我们发现,如果我们让next[7](str2字符"e"的位置)指向next[3](str2字符"d"的位置),那么,这样我们可以在上述匹配失败的时候让str2从第四个字符重新开始匹配,而不是回到第1个字符
而这个字符'd'的位置,正好就是字符'e'的前缀和后缀相同的字符数(都是"abc"),也就是当'e'匹配失败后就跳到'd'
以下内容转自阮一峰的网络日志
字符串匹配是计算机的基本任务之一。
举例来说,有一个字符串"BBC ABCDAB ABCDABCDABDE",我想知道,里面是否包含另一个字符串"ABCDABD"?

许多算法可以完成这个任务,Knuth-Morris-Pratt算法(简称KMP)是最常用的之一。它以三个发明者命名,起头的那个K就是著名科学家Donald Knuth。

这种算法不太容易理解,网上有很多解释,但读起来都很费劲。直到读到Jake Boxer的文章,我才真正理解这种算法。下面,我用自己的语言,试图写一篇比较好懂的KMP算法解释。
1.

首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位。
2.

因为B与A不匹配,搜索词再往后移。
3.

就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止。
4.

接着比较字符串和搜索词的下一个字符,还是相同。
5.

直到字符串有一个字符,与搜索词对应的字符不相同为止。
6.

这时,最自然的反应是,将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍。
7.

一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是,设法利用这个已知信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。
8.

怎么做到这一点呢?可以针对搜索词,算出一张《部分匹配表》(Partial Match Table)。这张表是如何产生的,后面再介绍,这里只要会用就可以了。
9.

已知空格与D不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的"部分匹配值"为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 6 - 2 等于4,所以将搜索词向后移动4位。
10.

因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2("AB"),对应的"部分匹配值"为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移2位。
11.
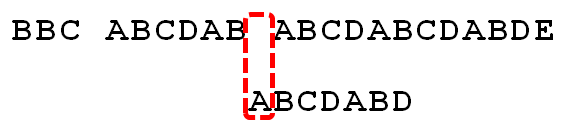
因为空格与A不匹配,继续后移一位。
12.

逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位。
13.

逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。
14.

下面介绍《部分匹配表》是如何产生的。
首先,要了解两个概念:"前缀"和"后缀"。 "前缀"指除了最后一个字符以外,一个字符串的全部头部组合;"后缀"指除了第一个字符以外,一个字符串的全部尾部组合。
15.

"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,
- "A"的前缀和后缀都为空集,共有元素的长度为0;
- "AB"的前缀为[A],后缀为[B],共有元素的长度为0;
- "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
- "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
- "ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1;
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB",长度为2;
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。
16.

"部分匹配"的实质是,有时候,字符串头部和尾部会有重复。比如,"ABCDAB"之中有两个"AB",那么它的"部分匹配值"就是2("AB"的长度)。搜索词移动的时候,第一个"AB"向后移动4位(字符串长度-部分匹配值),就可以来到第二个"AB"的位置。
以下是模板
void Find_Next(){
nexta[0] = -1;
nexta[1] = 0;
int cnt = 0;
int leng = strlen(s2);
int i = 2;
while(i<=leng){
if(s2[i-1]==s2[cnt])
nexta[i++] = ++ cnt;
else if(cnt>0)
cnt = nexta[cnt];
else
nexta[i++] = 0;
}
}
int kmp(){ //x为str1的长度,y为str2的长度,i为str1的下标,j为str2的下标
int i,j;
i = j = 0;
if(x<y)
return -1;
while(i<x&&j<y){
if(j==-1||s1[i]==s2[j])
i++,j++;
else
j = nexta[j];
}
if(j==y)
return i-j+1;
else
return -1;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号