某些神奇的结论/套路

• 对于一个 DAG 的所有拓扑序中字典序最大的拓扑序，它的逆也是最大的。
• dilworth 定理和它的对偶定理：DAG 的最小链覆盖 = 最长反链，最长链 = 最小反链覆盖。
• 判断图删点后是否联通：给非树边定随机权值，树边权值为覆盖它的非树边 \(\text{xor}\) 和，判断删去的边是否线性无关。
• Konig 定理求二分图的最小点覆盖：求出最大匹配后，从右侧每个非匹配点出发走增广路，标记路上经过的点，取右侧的非标记点和左侧的标记点。
• 求序列冒泡排序 \(k\) 轮后的结果：维护小根堆，从左到右扫，遇到元素放入堆内，如果堆大小 \(>k\) 或已经扫完整个序列就弹出堆顶并插入答案序列尾部。
• 没有值域连续段的排列个数的生成函数和 \(\sum\limits_{i\gt 1}i!x^i\) 的复合逆非常像。
• \(\sum\limits_{i=1}^n i^m = \frac{1}{m+1}\sum\limits_{i=0}^m\left(-1\right)^i\binom{m+1}{i} B_i n^{m-i+1}\)，其中 \(B\) 为伯努利数，指数生成函数为 \(\frac{x}{e^x-1}\)
• CDQ 分治是可以直接搬到树上的（即求祖先对后代的影响）。
• 非齐次线性递推式的解 = 非齐次线性递推式的特解 + 齐次线性递推式的通解
• 二分图所有最大匹配中出现过的点的交 = 二分图所有最小点覆盖的并
• 二分图最大匹配 = \(n-\max\limits_{S\subseteq V_l}\left(\left|S\right| - \left|N\left(S\right)\right|\right)\)
• 竞赛图性质：缩点之后是链；\(n\) 阶强联通竞赛图对于 \(3\le i\le n\) 存在大小为 \(i\) 的环。
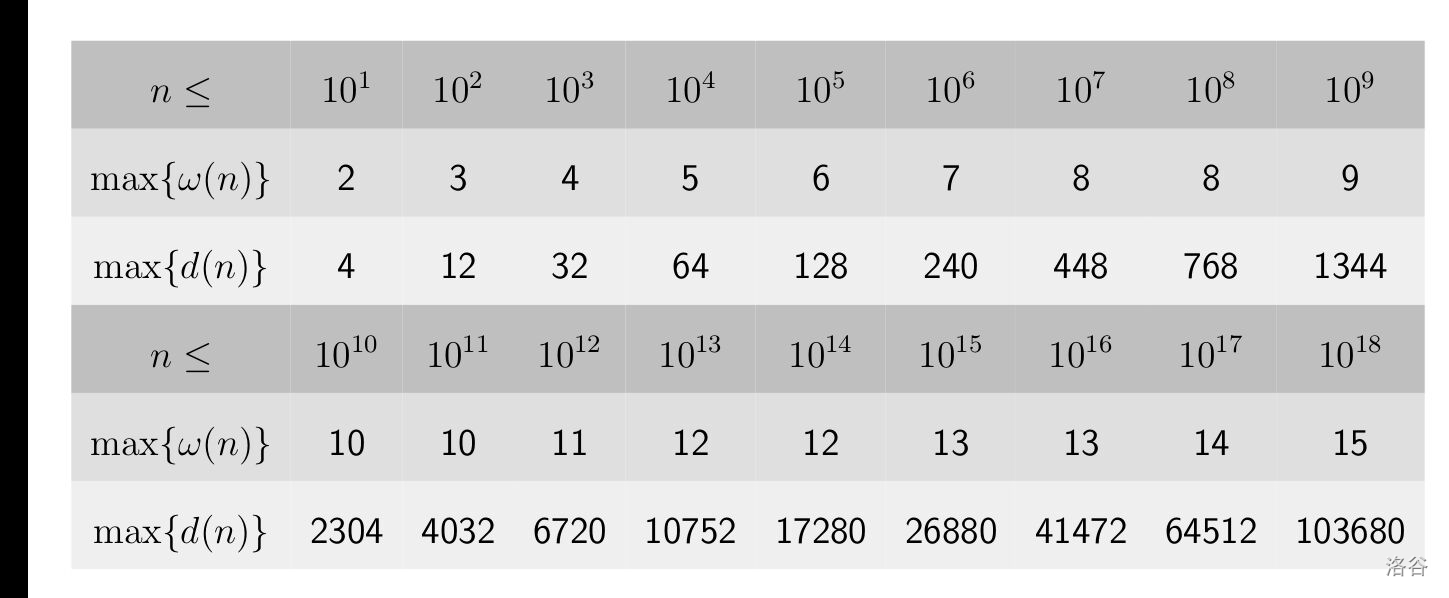
• \(n\) 较小时，\(\max_{i=1}^n\sigma_0\left(i\right)\approx n^{\frac{1.066}{\ln\ln n}}\)。下图是 \(n\le 10^{18}\) 时更精确的结果：
• 对于某种构造题，如果是给个初态和固定终态，操作可逆，那么相当于无向图上问和某个点的连通性，如果任意状态可以进行的操作都比较多，且没有操作前后恒定不变的量（如 xor 和等），那么规模大时可能会一定有解。可以暴搜小的情况，找到一个全部有解的临界点，然后对大的情况进行归纳。例：CF1031E/某联考题
• 两个博弈的差博弈后手必胜则这两个博弈等价。
• 杨表性质：标准杨表方案数为 \(\frac{n!}{\prod\limits_{x\in Y}{\text{hook}\left(x\right)}}\)；行严格单调增而列不严格单调增的斜杨表方案数为 \(\prod\limits_{\left(i,j\right)\in Y}\frac{r+j-i}{\text{hook}\left(x\right)}\)；\(n\) 阶杨表总数等于对合数；\(n\) 阶杨表有序对与 \(n\) 阶排列一一对应；如果把插入时判定条件取反则杨表形状沿主对角线对称。
• 对 \(n\) 个点建 \(k\) 维 KD-tree 后定位 \(k\) 维矩形的复杂度为 \(O\left(n^{\frac{k-1}{k}}\right)\)。
• min-max 容斥：\(\max_k\left(S\right)=\sum\limits_{T\subseteq S,\left|T\right|\ge k}\left(-1\right)^{\left|T\right|-k}\binom{\left|T\right|-1}{k-1}\min\left(T\right)\)
• 斯特林公式：\(n!\sim\sqrt{2\pi n}\left(\frac{n}{\mathrm{e}}\right)^n\left(1+\frac{1}{12n}\right)\)
• 整数拆分：\(p\left(n\right)\sim\frac{1}{4\sqrt{3}n}\exp\left(\pi\sqrt{\frac{2n}{3}}\right)\)
• 扩展拉格朗日反演：若 \(F\left(G\left(x\right)\right)=x\)，则 \(\left[x^n\right]H\left(F\left(x\right)\right) = \frac{1}{n}\left[x^{n-1}\right]H'\left(x\right)\left(\frac{x}{G\left(x\right)}\right)^n\)
• 另类拉格朗日反演：若 \(F\left(G\left(x\right)\right)=x\)，则 \(\left[x^n\right]H\left(F\left(x\right)\right) = \left[x^n\right]H\left(x\right)G'\left(x\right)\left(\frac{x}{G\left(x\right)}\right)^{n+1}\)
• 周期引理：若 \(p,q\) 为字符串 \(S\) 的周期且 \(p+q-\gcd\left(p,q\right)\le \left|S\right|\)，则 \(\gcd\left(p,q\right)\) 也是 \(S\) 的周期。
• 五边形数定理：\(\prod\limits_{i\ge 1}\left(1-x^i\right)=\sum\limits_{i\in\mathbb{Z}}\left(-1\right)^ix^{\frac{i\left(3i+1\right)}{2}}\)
• \(\binom{n+m}{n}\) 的质因子分解中 \(p\) 的幂次为 \(p\) 进制下 \(n\) 与 \(m\) 做加法时的进位次数。
• \(GF\left(q\right)\) 上次数整除 \(n\) 的首一不可约多项式乘积为 \(x^{q^n}-x\)。
• \(\frac{1}{\sqrt{1-4x}}=\sum\limits_{i\ge 0}\binom{2i}{i}x^i\)
• \(\left(\frac{1-\sqrt{1-4x}}{2x}\right)^k=\sum\limits_{i\ge 0}\left(\binom{2i+k-1}{i}-\binom{2i+k-1}{i-1}\right)x^i\)
• \(\frac{1}{\sqrt{1-4x}}\left(\frac{1-\sqrt{1-4x}}{2x}\right)^k=\sum\limits_{i\ge 0}\binom{2i+k}{i}x^i\)
• Chung-Feller 定理：\(\left(n,m\right)-Dyck\) 路的个数与 \(m\) 无关，且都等于第 \(n\) 个卡特兰数。
• 有理根定理：整系数方程 \(\sum\limits_{i=0}^na_ix^i=0\) 的有理根 \(x=\frac{p}{q}\) 满足 \(p\vert a_0, q\vert a_n\)。
• 系数矩阵为满秩稀疏矩阵时解方程组：实质上是求列向量乘稀疏矩阵的逆。设矩阵大小为 \(n\times n\)，非零位置有 \(m\) 个。可以对 \(A^k\left(0\le k\le 3n\right)\) 随机右乘行向量再左乘列向量，跑 BM 得到其零化多项式，得到它的逆与 \(A^k\left(0\le k\le n\right)\) 之间的等式，再分别乘列向量。时间复杂度 \(O\left(nm\right)\)。
• 长度之和为 \(n\) 的不同的串在长度为 \(m\) 的串的 SAM 上 endpos 集合大小的和不超过 \(O\left(m\sqrt{n}\right)\)。
• \(n\) 以内最大质数间隔至少为 \(O\left(\frac{\log n\log\log n\log\log\log\log n}{\log\log\log n}\right)\)。
• 联通图删掉若干条边后为二分图，当且仅当给每条非树边对应的环一个线性无关的权值后删去的边 xor 和 = 所有边 xor 和。