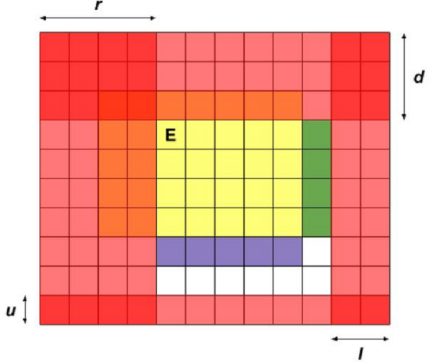
E - Salvage Robots
动多个机器人可以看作动一个出口。
出口回收范围一定是一个矩形，任存在的机器人范围也是矩形。
dp状态存出口矩形四个方向的延伸量，每次某方向上扩展一格。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 105;
char s[N][N];
int sh[N][N], sl[N][N], val[N][N];
short dp[105][105][105][105];
int main() {
int n, m; scanf("%d%d", &n, &m);
int ex, ey;
for(int i = 1; i <= n; i++) {
scanf("%s", s[i] + 1);
for(int j = 1; j <= m; j++) {
if(s[i][j] == 'E') {ex = i; ey = j;}
else if(s[i][j] == 'o') {sh[i][j] = sl[i][j] = 1;}
sh[i][j] += sh[i][j - 1]; sl[i][j] += sl[i - 1][j];
}
}
int ans = 0;
for(int l = 0; l <= ey - 1; l++) {
for(int r = 0; r <= m - ey; r++) {
for(int u = 0; u <= ex - 1; u++) {
for(int d = 0; d <= n - ex; d++) {
ans = max(ans, (int)dp[l][r][u][d]);
if(l + r < ey - 1) {dp[l + 1][r][u][d] = max((int)dp[l + 1][r][u][d], dp[l][r][u][d] + sl[min(ex + d, n - u)][ey - l - 1] - sl[max(d, ex - u - 1)][ey - l - 1]);}
if(l + r < m - ey) {dp[l][r + 1][u][d] = max((int)dp[l][r + 1][u][d], dp[l][r][u][d] + sl[min(ex + d, n - u)][ey + r + 1] - sl[max(d, ex - u - 1)][ey + r + 1]);}
if(u + d < ex - 1) {dp[l][r][u + 1][d] = max((int)dp[l][r][u + 1][d], dp[l][r][u][d] + sh[ex - u - 1][min(ey + r, m - l)] - sh[ex - u - 1][max(ey - l - 1, r)]);}
if(u + d < n - ex) {dp[l][r][u][d + 1] = max((int)dp[l][r][u][d + 1], dp[l][r][u][d] + sh[ex + d + 1][min(ey + r, m - l)] - sh[ex + d + 1][max(ey - l - 1, r)]);}
}
}
}
}
printf("%d", ans);
return 0;
}
F - Namori
思路有点繁杂
首先是模型转换，树是二分图可黑白染色，转换为相邻不同黑白交换问题，或者是把黑看作棋子白看作空位的移棋子问题。
- 树，\(a(i)\) 表示子树内的黑白差，\(i\) 和 \(fa(i)\) 之间至少交换 \(|a(i)|\) 次，而发现可以取到这个下界（不会证），答案为 \(\sum|a(i)|\)。
- 偶环（可以二分图），设环上转移量为 \(x\) 数列，可以对每个点根据最终黑白差\(=0\)列方程，具体看上面博客，可以通过中位数得到最值，然后答案就是子树内部的 \(\sum|a(i)|\) 和 \(x\) 数列和。
- 奇环：非树边的作用是可以将两端同时反色，而这样就能改变黑白点数，所以操作次数固定为\(\frac{a(rt)}{2}\)， 这样可以直接改环上最深的那个点的\(a\)值。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6 + 5;
int a[N], head[N], to[N], nxt[N], ecnt, fa[N], b[N], lst[N], tot;
void add_edge(int u, int v) {nxt[++ecnt] = head[u]; to[ecnt] = v; head[u] = ecnt;}
int g_fa(int u) {return fa[u] == u ? u : fa[u] = g_fa(fa[u]);}
void dfs(int u, int op) {
a[u] = op;
for(int i = head[u]; i; i = nxt[i]) {
int v = to[i]; if(v == lst[u]) continue;
lst[v] = u; dfs(v, -op); a[u] += a[v];
}
}
int main() {
int n, m, rt = 1, ed; scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) fa[i] = i;
for(int i = 1; i <= m; i++) {
int u, v; scanf("%d%d", &u, &v);
int x(g_fa(u)), y(g_fa(v));
if(x == y) {rt = u; ed = v;}
else {fa[x] = y; add_edge(u, v), add_edge(v, u);}
}
// printf("!rt=%d ed=%d\n", rt, ed);
dfs(rt, 1);
if(n == m) {
for(int x = ed; x; x = lst[x]) {b[++tot] = a[x];}
//the times of (ed->rt) are add on a[rt]
if(tot & 1) {
if(a[rt] & 1) {puts("-1"); return 0;}
for(int x = ed; x; x = lst[x]) {a[x] -= a[rt] >> 1;}
}
else {
if(a[rt]) {puts("-1"); return 0;}
sort(b + 1, b + 1 + tot);
for(int x = ed; x; x = lst[x]) {a[x] -= b[tot >> 1];}
}
}
else if(a[rt]) {puts("-1"); return 0;}
ll ans = 0;
for(int i = 1; i <= n; i++) {ans += abs(a[i]);}
printf("%lld", ans);
return 0;
}
