description
有\(n\)封邮件,每封目标投到\(a_i\),不过不能直接投到,会有一个中转的过程(先投到邮箱里)。\(n\)个地方,每个地方有一个邮箱(很辣鸡最多只能放一封邮件),邮递员会把这个邮箱\(i\)里邮件投到\(b_i\)。
xzl很笨,于是问你\(q\)个询问,告诉你\([l1,r1]\),\([l2,r2]\)问邮件\([l1,r1]\)投进邮箱\([l2,r2]\)后能送到目标的期望邮件个数是多少。
solution
期望满足可加性,即求每个邮件能投中的概率和。
令\(c_i\)为\(b_{l2}...b_{r2}\)中等于\(a_i\)的个数。
每个邮件的概率为\(\frac{c_i}{r2-l2+1}\),你可以理解为乘法原理,满足条件的数量,和样本容量除了第一项(第一次让第\(i\)封邮件选择有\(c_i\)中满足),后面就类似下阶乘(无限)都是相同的。
\(ans=\frac{\sum\limits_{i=l1}^{r1}c_i}{r2-l2+1}\)
现在求分子这东西了,相当于求两个区间相等的对数。分块
1.分块 code
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
const int M=365;
int val[N],n,q,a[N],b[N],B[N],L[M],R[M],Blen,Btot;
int ca[M][N],cb[M][N],So[M][M],sa[N],sb[N],tota,totb;
bool ma[N],mb[N];
namespace IO {
char buf[1<<23],*p1=buf,*p2=buf;
#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
inline int rd() {
int x=0;char ch=gc();
while(!isdigit(ch)) {ch=gc();}
while(isdigit(ch)) {x=x*10+(ch^48);ch=gc();}
return x;
}
}
void init() {
int nn=0;
n=IO::rd();q=IO::rd();
Blen=(int)sqrt(n);
for(int i=1;i<=n;i++) {a[i]=IO::rd();}
for(int i=1;i<=n;i++) {b[i]=IO::rd();}
sort(val+1,val+1+nn);
nn=unique(val+1,val+1+nn)-val;
for(int i=1;i<=n;i++) {
a[i]=lower_bound(val+1,val+nn,a[i])-val;
if(!ma[a[i]]){sa[++tota]=a[i];ma[a[i]]=1;}
}
for(int i=1;i<=n;i++) {
b[i]=lower_bound(val+1,val+nn,b[i])-val;
mb[b[i]]=1;
}
for(int l=1,r;l<=n;l=r+1) {
r=min(l+Blen-1,n);++Btot;
// printf("#Btot=%d l=%d r=%d\n",Btot,l,r);
L[Btot]=l,R[Btot]=r;
for(int j=l;j<=r;j++) {B[j]=Btot;ca[Btot][a[j]]++;
// if(r==n)printf("ED j=%d (aj=%d,bj=%d)\n",j,a[j],b[j]);
cb[Btot][b[j]]++;}
}
for(int i=1;i<=Btot;i++) {
for(int j=1;j<=Btot;j++) {
So[i][j]=So[i][j-1];
for(int k=L[i];k<=R[i];k++) {
So[i][j]+=cb[j][a[k]];
}
}
}
for(int i=1;i<=Btot;i++) {
for(int j=1;j<=n;j++) ca[i][j]+=ca[i-1][j],cb[i][j]+=cb[i-1][j];
}
// printf("blen = %d btot = %d\n",Blen,Btot);
}
int cnt[N];
ll gcd(ll a,ll b) {return !b?a:gcd(b,a%b);}
ll P=0,Q=0;
void Query() {
int l1,l2,r1,r2;
ll ans=0;
l1=IO::rd();r1=IO::rd();l2=IO::rd(),r2=IO::rd();
int br=B[r2]-1,bl=B[l2],_br=B[r1]-1,_bl=B[l1];
bool f1=(_bl<_br),f2=(bl<br); //有无整块
if(f1&&f2)for(int i=B[l1]+1;i<B[r1];i++) {ans+=So[i][br]-So[i][bl];}
if(B[l1]==B[r1]) {
if(f2) for(int i=l1;i<=r1;i++){int va=a[i];ans+=cb[br][va]-cb[bl][va];cnt[va]++;}
else for(int i=l1;i<=r1;i++){cnt[a[i]]++;}
}
else {
int sl_1=R[B[l1]],_sr1=L[B[r1]];
if(f2) {
for(int i=l1;i<=sl_1;i++){int va=a[i];ans+=cb[br][va]-cb[bl][va];cnt[va]++;}
for(int i=_sr1;i<=r1;i++){int va=a[i];ans+=cb[br][va]-cb[bl][va];cnt[va]++;}
}
else {
for(int i=l1;i<=sl_1;i++){cnt[a[i]]++;}
for(int i=_sr1;i<=r1;i++){cnt[a[i]]++;}
}
}
if(B[l2]==B[r2]) {
if(!f1) for(int i=l2;i<=r2;i++){int vb(b[i]);ans+=cnt[vb];}
else for(int i=l2;i<=r2;i++){int vb=b[i];ans+=ca[_br][vb]-ca[_bl][vb]+cnt[vb];}
}
else {
int sl_2=R[B[l2]],_sr2=L[B[r2]];
if(f1) {
for(int i=l2;i<=sl_2;i++){int vb(b[i]);
ans+=ca[_br][vb]-ca[_bl][vb]+cnt[vb];}
for(int i=_sr2;i<=r2;i++){int vb(b[i]);
ans+=ca[_br][vb]-ca[_bl][vb]+cnt[vb];}
}
else {
for(int i=l2;i<=sl_2;i++) {
ans+=cnt[b[i]];}
for(int i=_sr2;i<=r2;i++){
ans+=cnt[b[i]];}
}
}
ll lb=r2-l2+1,d=gcd(ans,lb);
P^=ans/d,Q^=lb/d;
if(B[l1]==B[r1]) {
for(int i=l1;i<=r1;i++){cnt[a[i]]=0;}
}
else {
int sl_1=R[B[l1]],_sr1=L[B[r1]];
for(int i=l1;i<=sl_1;i++){cnt[a[i]]=0;}
for(int i=_sr1;i<=r1;i++){cnt[a[i]]=0;}
}
}
int main() {
// freopen("yangli.in","r",stdin);
init();
for(int i=1;i<=q;i++) Query();
printf("%lld %lld",P,Q);
return 0;
}
当然发现太劣了,跑不过,而且几乎不可能卡常卡过。
问了Eb,然后就知道了拼接\(a,b\)后容斥的做法。真的很厉害。
贺Eb的图:
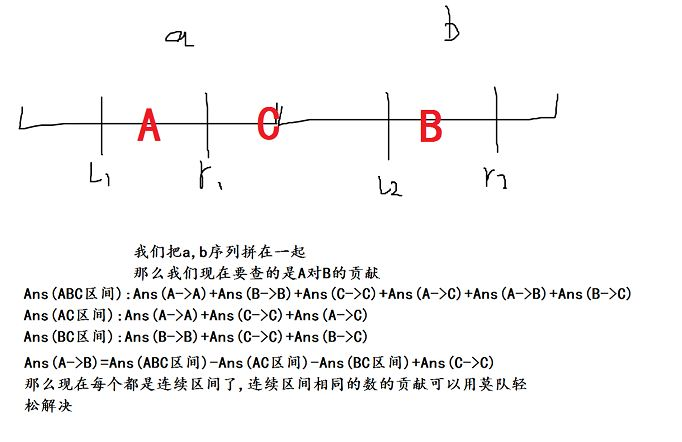
比分块快太多了。而且复杂度是跟\(n\)相关的,关键是超级好写呢。
2.莫队 code
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e6+5;
int a[N],B[N],Blen,tot,lenb[N],n,q,nn,val[N];
ll ans[N];
struct query{int id,l,r;}Q[N<<1];
bool cmp(query u,query v) {return B[u.l]==B[v.l]?u.r<v.r:B[u.l]<B[v.l];}
namespace IO {
char buf[1<<23],*p1=buf,*p2=buf;
#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
inline int rd() {
int x=0;char ch=gc();
while(!isdigit(ch)) {ch=gc();}
while(isdigit(ch)) {x=x*10+(ch^48);ch=gc();}
return x;
}
}
void init() {
n=IO::rd();q=IO::rd();
nn=n<<1;
Blen=225;
for(int i=1;i<=n;i++) {a[i]=IO::rd();B[i]=(i-1)/Blen+1;val[i]=a[i];}
for(int i=n+1;i<=nn;i++) {a[i]=IO::rd();B[i]=(i-1)/Blen+1;val[i]=a[i];}
sort(val+1,val+1+nn);
nn=unique(val+1,val+1+nn)-val;
for(int i=1;i<=(n<<1);i++) a[i]=lower_bound(val+1,val+nn,a[i])-val;
for(int i=1;i<=q;i++) {
int l1,l2,r1,r2;
l1=IO::rd(),r1=IO::rd(),l2=IO::rd(),r2=IO::rd();
lenb[i]=r2-l2+1;
l2+=n;r2+=n;
Q[++tot]=(query){i,l1,r2};if(r1+1<l2)Q[++tot]=(query){i,r1+1,l2-1};
Q[++tot]=(query){-i,l1,l2-1};Q[++tot]=(query){-i,r1+1,r2};
}
sort(Q+1,Q+1+tot,cmp);
}
int cnt[N],L=1,R=0;
ll res=0,X,Y;
ll gcd(ll a,ll b) {return !b?a:gcd(b,a%b);}
void Add(int x) {res+=cnt[x];cnt[x]++;}
void Del(int x) {cnt[x]--;res-=cnt[x];}
void modui() {
for(int i=1;i<=tot;i++) {
int l(Q[i].l),r(Q[i].r),opt=(Q[i].id<0)?-1:1;
while(L>l)Add(a[--L]);
while(R<r)Add(a[++R]);
while(L<l)Del(a[L++]);
while(R>r)Del(a[R--]);
ans[Q[i].id*opt]+=opt*res;
}
for(int i=1;i<=q;i++) {
ll p=ans[i],q=lenb[i],d=gcd(ans[i],lenb[i]);
X^=(p/d);Y^=(q/d);
}
printf("%lld %lld\n",X,Y);
}
int main() {
// freopen("data.in","r",stdin);
init();
modui();
return 0;
}

