CF 1015F

• 题意：[CF 1015F](https://codeforces.com/contest/1015/problem/F）
  给你一个模式串A（一个不一定合法的括号序列），让你构造长度为2*n的合法括号序列，问有多少种方案使得含A为其子串。(n<=100)
• 思路:
  KMP+DP
  \(dp[i][j][k][0/1]\)表示当前匹配到了\(a[i]\),\(s[j]\),此时左括号数-右括号数为\(k\),是否含有A的方案数。
  然后j->j+1,枚举j+1是'('还是')'，然后将其按照KMP匹配a。方程见代码。
• code:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=205;
const ll mod=1e9+7;
char s[N];
ll dp[N][N][N][2];
int n,len,a[N],nxt[N],to[N][3];
void init() {
	int j=0;
	for(int i=2;i<=len;i++) {
		while(j&&a[i]!=a[j+1])j=nxt[j];
		if(a[i]==a[j+1])j++;
		nxt[i]=j;
	} 
}
int Fld(int i,int c) {
	if(to[i][c+1]!=-1)return to[i][c+1];
	while(i&&a[i+1]!=c)i=nxt[i];
	return to[i][c+1]=i+(a[i+1]==c);
}

int main() {
	memset(to,-1,sizeof(to));
	scanf("%d",&n);
	scanf("%s",s+1);len=strlen(s+1);
	for(int i=1;i<=len;i++)a[i]=(s[i]=='(')?1:-1;
	init();
	dp[0][0][0][0]=1;
	for(int j=0;j<(n<<1);j++) {
		for(int i=0;i<=len;i++) {
			for(int k=0;k<=n;k++) {
				for(int f=0;f<=1;f++) {
					if(!dp[i][j][k][f])continue;  //优化
					if(k) {int t=Fld(i,-1);dp[t][j+1][k-1][f|(t==len)]=(dp[t][j+1][k-1][f|(t==len)]+dp[i][j][k][f])%mod;}
					if(k<n) {int t=Fld(i,1);dp[t][j+1][k+1][f|(t==len)]=(dp[t][j+1][k+1][f|(t==len)]+dp[i][j][k][f])%mod;}
				}
			}
		}
	}
	ll ans=0;
	for(int i=0;i<=len;i++) ans=(ans+dp[i][n<<1][0][1])%mod; 
	printf("%lld",ans);
	return 0;
} 
//5
//()))()

ps.大常数选手的一些不超时小优化
1.（必须加）：if(!dp[i][j][k][f])continue;因为有很多不可能的状态，大量优化时间。
2.记忆化Fld
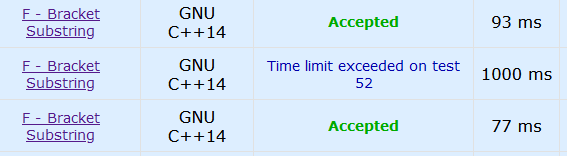
效果从下到上分别为：1+2，0，1