算法第二章上机实践报告
引论:通过学习第二章的知识,我掌握了算法中的一种典型解题思路——分治法,这种解题方法的妙处在于化复杂难解的大问题为一个个同类型的易解小问题,最后将所有小问题合并为原先的大问题,达到解决问题的目的。那么下面我选取了第二章中的实验的第二题为例子,分享我的学习心得。
一、实践题目
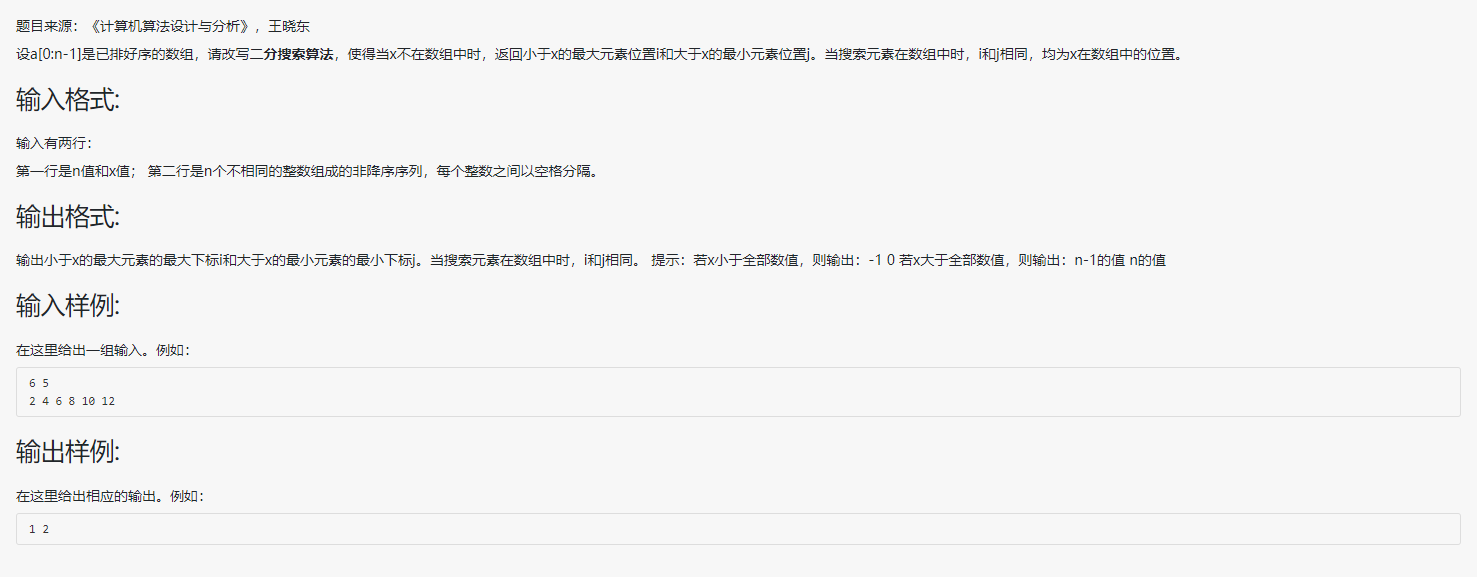
二、问题描述
本题的核心仍为二分搜索法,但本题的二分搜索相比书本上介绍的略有不同,因为题目需要我们分析可能出现的各种情况,现在我先列出各种可能的情况:
1.需要搜索的元素在所给的数组中。在这种情况下,我们仅需要用普通的二分搜索算法得出所得到要搜索之数在数组的下标。
2.需要搜索的元素不在所给的数组中,在这种情况下,还要细分为3种情况:
①需要搜索的元素比数组的任何一个数都小,则输出-1和0;
②需要搜索的元素比数组的任何一个数都大,则输出n-1和n(其中n为数组的长度);
③需要搜索的元素不在数组中,但其不大于数组最大值也不小于数组最小值,则要输出小于x的最大元素位置i和大于x的最小元素位置j。
因此,我们需要在这算法中将这所有情况一一列举出来,并分条件将其解决。
三、算法描述
先分享一下我解决这题的代码;
int binarySearch(int a[], int x, int n, int &i, int &j) { int left = 0; int right = n - 1; bool flag = false; //设立一个检测值,方便我们分析当元素不在数组中的情况 int m = 0; while (left <= right) { int middle = (left + right) / 2; m = middle; //m用于保存二分搜索中最后一次middle值 if (x == a[middle]) //二分搜索中找到所需元素的情况 { i = middle; j = i; return i; } else if (x < a[middle]) //二分搜索中,若搜索值比中间值大,则缩减搜索的最大值 { right = middle - 1; } else if (x > a[middle]) //二分搜索中,若搜索值比中间值小,则增大搜索的最小值 { left = middle + 1; } flag = true; //检测值设为真,则开始分析元素不在数组中的情况 } if (flag) { if (x > a[0] && x < a[n - 1]) //若搜索值在数组中不大于最大值、不小于最小值 { if (x > a[m]) //其中若搜索值大于循环中的最后一次middle值,则有以下情况 { i = m; j = m + 1; } else //其中若搜索值小于循环中的最后一次middle值,则有以下情况 { i = m - 1; j = m; } } else if (x < a[0]) //若搜索值小于数组最小值,则输出-1与0 { i = -1; j = 0; } else //若搜索值小于数组最小值,则输出n-1与n { i = n - 1; j = n; } } }
在设计这个算法之前,我用了多组数据测试了当“需要搜索的元素不在数组中,但其不大于数组最大值也不小于数组最小值,则要输出小于x的最大元素位置i和大于x的最小元素位置j。”的这种情况,在草稿测试后,得出结论:在这种情况下,当需要搜索的元素大于最后的一次a[middle],则i和j分别是m和m+1;当需要搜索的元素小于最后的一次a[middle],则i和j分别是m-1和m。
其次,对于需要搜索的元素不在所给的数组中的这种情况,我设置了一个flag监测点,当目标元素查不到时,这个flag就变为真开始分析这是需要搜索的元素不在所给的数组中的哪一种具体情况。而针对能查找到目标元素的情况,则仅需传统的使用二分搜索即可,但必须设定一个return出口,否则会出现死循环情况。
四、算法时间及空间复杂度分析
对于时间复杂度:由于本题的核心算法是由二分搜索法改造而来的,其核心部分(能在数组中找到目标元素)没有发生改变,仅仅是在找不到目标元素的情况下,增加了判断分析,而这些判断分析也只是将i和j赋值,因此仅分析核心部分的时间复杂度即可。而核心部分是传统的二分搜索法,因为将数组折半搜索,因此每次搜索都是分成两半,所以时间复杂度是以2为底的系数,因此可以知道本算法的时间复杂度为O(logn)。
对于空间复杂度:本算法所用到的数组仅仅是传入进来的形参,处理main函数中定义的与题目要求一致的数组,没有额外分配空间给另外的数组,也没有需要定义另外的数组,同时,本算法仅仅是多定义了五个变量left、right、middle、flag、m分别存储数组的最小值下标、最大值下标、一次二分搜索后的下标、检测值、当前的middle值,而这些变量不需要额外分配内存空间,因此空间复杂度为O(1)。
五、心得体会
通过编程来解决这一道题给我的收获是很多的,首先这一个算法是用书本上提供的传统二分搜索算法来改造而成的,而正是这一个算法能够解决这样一个实际问题,因此,很多好用、有深度的算法,其内核往往是能够让人明白的,只是根据实际情况来改装的,所以我们首先要深刻理解一个典型的算法,再实事求是来改装典型的算法用于解决实际问题。
其次,通过编程解决这道问题给了我想要继续钻研算法的信心,因为这道题我是和搭档一起想出来的,一起通过测试多个数组来分析出各种情况,能够独立思考出一道题并将其解决的感觉真好!
对于算法实验课,二人小组合作是非常重要的,因为一个人的编程能力再强,也会有疏漏的地方,如果有搭档帮忙检查代码,并一起分析解题关键步骤,那么难题就会迎刃而解了!
通过本次实验,我希望自己能够再接再厉,不断钻研算法知识,争取解决更多的问题!



