东拼西凑的模板·持续更新中

一.常用算法

文中代码大量来自ACM算法模板 · 一些常用的算法模板-模板合集（稍加修改）

 

1.1 快速幂

ll qpow(ll x, ll n , ll mod)
{
    ll ans=1;
    while(n){
        if(n&1){
            ans=(ans*x)%mod;
            n--;
        }
        x=(x*x)%mod;
        n>>=1;
    }
    return ans;
}

 

1.2 gcd

ll gcd(ll a,ll b){
    return b==0?a:gcd(b,a%b);
}

 1.3 大数乘法

long long quick_multiply(long long a, long long b, long long mod) {
    long long result = 0;
    while (b) {
        result = (result + (b % 2 * a) % mod) % mod;
        a = a * 2 % mod;
        b = b / 2;
    }
}

for(i=0; i<LA-1; i++)
    for(j=0; j<LB-1; j++)
        c[i+j]+=a[i]*b[j];

for(i=0; i<LA+LB; i++)
    if(c[i]>=10)
    {
        c[i+1]+=c[i]/10;
        c[i]%=10;
    }

//https://www.cnblogs.com/king-ding/p/bigIntegerMul.html
#include<stdio.h>
#include<string.h>
#include<malloc.h>

#define and &&           /**************/
#define or ||            /* python风格 */
#define not !            /*            */
#define Int(X) (X - '0') /**************/

int *multiBigInteger(const char *, const char *);
int checkNum(const char *);

int main(void)
{
    char num1[100] = {'\0'}, num2[100] = {'\0'};
    printf("Please input two nunber(less than 100 digits):\n> ");
    while(scanf("%s%s", num1, num2) != EOF)
    {
        int *result = NULL;
        int i, change = 0;
        //对输入的数据进行检验
        if(strlen(num1) > 100 or strlen(num2) > 100)
        {
            printf("per number must less than 100 digits\n");
            return 1;
        }

        if(checkNum(num1) or checkNum(num2))
        {
            printf("ERROR: input must be an Integer\n");
            return 1;
        }

        printf("num1:\t%s\nnum2:\t%s\n", num1, num2);

        result = multiBigInteger(num1, num2);

        /* 输出结果result，result[0]保存着result的长度，
         * 所以下标要从1开始 */
        printf("result:\t");
        for(i = 1; i <= result[0]; i++)
        {
            if(result[i] != 0) //这一步用来去掉前导0,第一位为0跳过不输出
                change = 1;
            if(not change)
            {
                if(i > 1)        //这一步用来判断结果是否为0,
                    {                //如果结果第二位还是0,就判断为0
                        printf("0");
                        break;
                    }
                continue;
            }
            printf("%d", result[i]);
        }
        printf("\n");
        printf("\nPlease input two nunber(less than 100 digits):\n> ");
    }
    return 0;
} 

//用于检测输入的是否是数字，如果是就返回0,不是就返回1
int checkNum(const char *num)
{
    int i;
    for(i = 0; (size_t)i < strlen(num); i++)
    {
        if(num[i] < '0' or num[i] > '9')
        {
            return 1;
        }
    }
    return 0;
}

//返回结果result，为一片内存块，类似数组
int *multiBigInteger(const char *num1, const char *num2)
{
    int *result = NULL;                //用来保存最终结果
    int num1Len = strlen(num1);        //num1的长度
    int num2Len = strlen(num2);        //num2的长度
    int resultLen;                     //结果的最大长度
    int i, j;                          //循环计数器
    resultLen = num1Len + num2Len;     //结果长度最大为num1长度和num2长度之和
    //初始化result为0
    result = (int *)malloc((resultLen+1)*sizeof(int));
    memset(result, 0, (resultLen+1)*sizeof(int));

    result[0] = resultLen; //result的第一位是用来保存result的长度的。
    /* num1乘以num2,由于这里采用先不进位的算法，所以算法是按从左到右
     * 按顺序来乘，然后将每位的结果保存到result的每一位中，循环一次
     * reult就从下一位开始求和。如下：(左边为正常算法，右边为本程序算法)
     *
     *     54321     |     54321
     *    ×  123     |    ×  123
     *    -------    |   --------
     *    162963     |     54321
     *   108642      |     108642
     *   54321       |      162963
     *   --------    |   ---------
     *   6681483     |     6681483
     *
     * */
    for(j = 0; j < num2Len; j++)
    {
        for(i = 0; i < num1Len; i++)
        {
            /* result第一位是用来保存result长度的，而第二位是保存结果最后的进位的
             * 没有进位，则result[1]为0，所以每位相乘之和是从第三位（即result[2]）
             * 开始。这里是本程序的比较巧妙的地方，需要仔细想想。
             * */
            result[i+j+2] += Int(num1[i]) * Int(num2[j]);
        }
    }

    /* 这个循环用来处理进位的，所以要从result的最后一位一直处理到首位。
     * 要注意result的总长度是resultLen+1,有一位是保存result的长度，而
     * C语言下标是从0开始，所以result的最后一位的下标就是resultLen，而
     * 第一位就是1。*/
    for(i = resultLen; i > 1; i--)
    {
        result[i-1] += result[i]/10;
        result[i] = result[i]%10;
    }
    printf("num1Len:%d\nnum2Len:%d\n", num1Len, num2Len);
    return result;
}

大整数相乘2完整代码

//JAVA 大数相乘 
import java.math.BigInteger;
import java.util.*;
import java.io.*;

public class Main
{
    public static void main(String args[])
    {
        Scanner cin = new Scanner(System.in);
            BigInteger a = cin.nextBigInteger();
            BigInteger b = cin.nextBigInteger();
            BigInteger ans = a.multiply(b);
            System.out.println(ans);
    }
}

1.4高精度幂运算

//JAVA 高精度幂 
import java.io.*;
import java.math.BigDecimal;
import java.util.*;

public class Main
{
    public static void main(String args[])
    {
        Scanner cin = new Scanner(System.in);    
        while(cin.hasNext())
        {
            BigDecimal ans = cin.nextBigDecimal();
            int n = cin.nextInt();
            String res = ans.pow(n).stripTrailingZeros().toPlainString(); //整数去掉后面的0和小数点 
            if(res.startsWith("0")) //去掉前导0 
            {
                res = res.substring(1);
            }
            System.out.println(res);
        }
    }
}

 更多java大数使用见：https://blog.csdn.net/morejarphone/article/details/51884888

1.6 二分查找

int l=0,r=n;
    while(l+1<r){
        int k=l+r>>1;
        if(check(k))l=k;
        else r=k;
    }

1.7 矩阵快速幂

struct Matrix {
    ll mat[3][3];
};

Matrix mul(Matrix a, Matrix b) {
    Matrix ret;
    for (int i = 0; i < 3; i++)
        for (int j = 0; j < 3; j++) {
            ret.mat[i][j] = 0;
            for (int k = 0; k < 3; k++) {
//                if(ret.mat[i][k]&&ret.mat[k][j])
                    ret.mat[i][j] = (ret.mat[i][j] + a.mat[i][k] * b.mat[k][j] % mod) % mod;
            }
        }
    return ret;
}

Matrix qpow(Matrix a, ll n) {
    Matrix ret;
    memset(ret.mat, 0, sizeof(ret.mat));
    ret.mat[0][0] = ret.mat[1][1] = ret.mat[2][2] = 1;
    Matrix tmp = a;
    while (n) {
        if (n & 1)ret = mul(ret, tmp);
        tmp = mul(tmp, tmp);
        n >>= 1;
    }
    return ret;
}

 

//https://blog.csdn.net/wust_zzwh/article/details/52058209
const int N=10;
int tmp[N][N];
void multi(int a[][N],int b[][N],int n)
{
    memset(tmp,0,sizeof tmp);
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
        for(int k=0;k<n;k++)
        tmp[i][j]+=a[i][k]*b[k][j];
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
        a[i][j]=tmp[i][j];
}
int res[N][N];
void Pow(int a[][N],int n)
{
    memset(res,0,sizeof res);//n是幂，N是矩阵大小
    for(int i=0;i<N;i++) res[i][i]=1;
    while(n)
    {
        if(n&1)
            multi(res,a,N);//res=res*a;复制直接在multi里面实现了；
        multi(a,a,N);//a=a*a
        n>>=1;
    }
}

#include"bits/stdc++.h"
#define vec vector<long long>
#define Mt  vector<vec>
using namespace std;
const int mod = 1e9 + 7;
int n;

Mt mul(Mt &A,Mt &B){
    Mt C(A.size(),vec(B[0].size()));
    for(int i=0;i<A.size();i++)
        for(int j=0;j<B[0].size();j++)
        for(int k=0;k<B.size();k++)
        C[i][j]=(C[i][j]+A[i][k]*B[k][j])%mod;
    return C;
}

long long qpow(long long x,long long n)
{
    long long ans=1;
    while(n){
        if(n&1){
            ans=(ans*x)%mod;
        }
        n>>=1;
        x=(x*x)%mod;
    }
    return ans;
}


Mt qpow(Mt A,long long n){
    Mt B(A.size(),vec(A.size()));
    for(int i=0;i<A.size();i++)
        B[i][i]=1;
    for(;n;n>>=1){if(n&1)B=mul(B,A);A=mul(A,A);}
    return B;
}

int main(){
    while(cin>>n){
        Mt X(4,vec(4));Mt Y(1,vec(4));Mt A(1,vec(5));Mt C(1,vec(5));
        X[0][0]=1; X[0][1]=1;X[1][2]=1;X[2][0]=1; X[2][3]=1;X[3][0]=1;
        Y[0][0]=6;Y[0][1]=4;Y[0][2]=2;Y[0][3]=1;
        A[0][0]=17,A[0][1]=7,A[0][2]=2,A[0][3]=0;A[0][4]=0;
        if(n<=5){
            printf("%lld\n",A[0][5-n]);
        }
        else{
            X=qpow(X,n-3);
            C=mul(Y,X);
            printf("%lld\n",(qpow(2,n)-C[0][0]+mod)%mod );
        }
    }
    return 0;
}

 1.8逆序数（归并排序）

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define ll long long
using namespace std;
const int N=1e6+5;
int f[N],t[N];
ll ans;
void Merge(int l,int m,int r) //左右两个表合并成一个表
{
    int i=l,j=m+1,cnt=0;
    while(i<=m && j<=r)
    {
        if(f[i]<=f[j])
            t[cnt++]=f[i++];
        else
        {
            ans+=m-i+1;
            t[cnt++]=f[j++]; //核心代码，求解逆序数个数。
        }
    }
    while(i<=m) //若左表不空
        t[cnt++]=f[i++];
    while(j<=r) //若右表不空
        t[cnt++]=f[j++];
    for(int k=0;k<cnt;) //修改原数组
        f[l++]=t[k++];
}
void Merge_sort(int l,int r) //归并排序
{
    if(l==r)
        return ;
    else
    {
        int m=(l+r)>>1;
        Merge_sort(l,m);
        Merge_sort(m+1,r);
        Merge(l,m,r);
    }
}
int  main()
{
    int n;
    ll x,y;
    while(scanf("%d%lld%lld",&n,&x,&y)==3)
    {
        for(int i=0;i<n;i++) scanf("%d",&f[i]);
        ans=0;
        Merge_sort(0,n-1);
        printf("%lld\n",min<ll>(x,y)*ans);
    }
    return 0;
}

 1.9 全排列遍历

STL的全排列支持可重集
int n;
int p[maxn];
void solve()
{
    scanf("%d",&n);
    for(int i = 0;i<n;i++)
    {
        scanf("%d",&p[i]);
    }
    do
    {
        for(int i = 0;i<n;i++) printf("%d ",p[i]);
        printf("\n");

    }while(next_permutation(p,p+n));
}

 1.10 lowbit(二进制最低位）

int lowbit(int x){    return x&(-x);    }

 1.11 组合数打表预处理

void init()
{
    Q[0]=1,Q[1]=2;
    C[1][0] = C[1][1] = 1;
    for (int i = 2; i < 110; i++)
    {
        Q[i] = Q[i-1]*2;
        C[i][0] = 1;
        for (int j = 1; j < 110; j++)
            C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
    }
}

 1.12 求逆元

lint ex_gcd(lint a,lint b,lint &x,lint &y)//扩展欧几里得（扩展gcd）
{
    if (a==0&&b==0) return -1;
    if (b==0){x=1;y=0;return a;}
    lint d=ex_gcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}
 
lint mod_inverse(lint a,lint n)//乘法逆元
{
    lint x,y;
    lint d = ex_gcd(a,n,x,y);
    return (x%n+n)%n;
}

int find(int x)  
{  
    int k=mod-2,ans=1;  
    while(k)  
    {  
        if (k&1) ans=(lint)ans*x%mod;  
        x=(lint)x*x%mod;  
        k>>=1;  
    }  
    return ans;  
}  x在%mod下的逆元

 

 

二.素数

2.1 素数筛

const int MAX = 100;
//快速素数筛，只筛选小于等于素数i的素数与i的乘积，既不会造成重复筛选，又不会遗漏。时间复杂度几乎是线性的。
//模板来源https://blog.csdn.net/stack_queue/article/details/53560887
long long su[MAX],cnt;
bool isprime[MAX];
void prime()
{
    cnt=1;
    memset(isprime,1,sizeof(isprime));//初始化认为所有数都为素数
    isprime[0]=isprime[1]=0;//0和1不是素数
    for(long long i=2;i<=MAX;i++)
    {
        if(isprime[i])
            su[cnt++]=i;//保存素数i
        for(long long j=1;j<cnt&&su[j]*i<MAX;j++)
        {
            isprime[su[j]*i]=0;//筛掉小于等于i的素数和i的积构成的合数
        }
    }
}
int main()
{
    prime();
    for(long long i=1;i<cnt;i++)
        printf("%d  ",su[i]);
    return 0;
}

2.2 米勒罗宾素数测试

//https://blog.csdn.net/u013654696/article/details/40056179
// 18位素数：154590409516822759
// 19位素数：2305843009213693951 (梅森素数)
// 19位素数：4384957924686954497
LL prime[6] = {2, 3, 5, 233, 331};
LL qmul(LL x, LL y, LL mod) { // 乘法防止溢出， 如果p * p不爆LL的话可以直接乘； O(1)乘法或者转化成二进制加法


    return (x * y - (long long)(x / (long double)mod * y + 1e-3) *mod + mod) % mod;
    /*
    LL ret = 0;
    while(y) {
        if(y & 1)
            ret = (ret + x) % mod;
        x = x * 2 % mod;
        y >>= 1;
    }
    return ret;
    */
}
LL qpow(LL a, LL n, LL mod) {
    LL ret = 1;
    while(n) {
        if(n & 1) ret = qmul(ret, a, mod);
        a = qmul(a, a, mod);
        n >>= 1;
    }
    return ret;
}
bool Miller_Rabin(LL p) {
    if(p < 2) return 0;
    if(p != 2 && p % 2 == 0) return 0;
    LL s = p - 1;
    while(! (s & 1)) s >>= 1;
    for(int i = 0; i < 5; ++i) {
        if(p == prime[i]) return 1;
        LL t = s, m = qpow(prime[i], s, p);
        while(t != p - 1 && m != 1 && m != p - 1) {
            m = qmul(m, m, p);
            t <<= 1;
        }
        if(m != p - 1 && !(t & 1)) return 0;
    }
    return 1;
}

 2.3 分解质因数

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<time.h>
#include<iostream>
#include<algorithm>
#include <map>
using namespace std;

map<int,int> mp;
map<int,int>::iterator it;
//****************************************************************
// Miller_Rabin 算法进行素数测试
//速度快，而且可以判断 <2^63的数
//****************************************************************
const int S=100;//随机算法判定次数，S越大，判错概率越小


//计算 (a*b)%c.   a,b都是long long的数，直接相乘可能溢出的
//  a,b,c <2^63
long long mult_mod(long long a,long long b,long long c)
{
    a%=c;
    b%=c;
    long long ret=0;
    while(b)
    {
        if(b&1){ret+=a;ret%=c;}
        a<<=1;
        if(a>=c)a%=c;
        b>>=1;
    }
    return ret;
}



//计算  x^n %c
long long pow_mod(long long x,long long n,long long mod)//x^n%c
{
    if(n==1)return x%mod;
    x%=mod;
    long long tmp=x;
    long long ret=1;
    while(n)
    {
        if(n&1) ret=mult_mod(ret,tmp,mod);
        tmp=mult_mod(tmp,tmp,mod);
        n>>=1;
    }
    return ret;
}





//以a为基,n-1=x*2^t      a^(n-1)=1(mod n)  验证n是不是合数
//一定是合数返回true,不一定返回false
bool check(long long a,long long n,long long x,long long t)
{
    long long ret=pow_mod(a,x,n);
    long long last=ret;
    for(int i=1;i<=t;i++)
    {
        ret=mult_mod(ret,ret,n);
        if(ret==1&&last!=1&&last!=n-1) return true;//合数
        last=ret;
    }
    if(ret!=1) return true;
    return false;
}

// Miller_Rabin()算法素数判定
//是素数返回true.(可能是伪素数，但概率极小)
//合数返回false;

bool Miller_Rabin(long long n)
{
    if(n<2)return false;
    if(n==2)return true;
    if((n&1)==0) return false;//偶数
    long long x=n-1;
    long long t=0;
    while((x&1)==0){x>>=1;t++;}
    for(int i=0;i<S;i++)
    {
        long long a=rand()%(n-1)+1;//rand()需要stdlib.h头文件
        if(check(a,n,x,t))
            return false;//合数
    }
    return true;
}


//************************************************
//pollard_rho 算法进行质因数分解
//************************************************
long long factor[10000];//质因数分解结果（刚返回时是无序的）
int tol;//质因数的个数。数组小标从0开始

long long gcd(long long a,long long b)
{
    if(a==0)return 1;//???????
    if(a<0) return gcd(-a,b);
    while(b)
    {
        long long t=a%b;
        a=b;
        b=t;
    }
    return a;
}

long long Pollard_rho(long long x,long long c)
{
    long long i=1,k=2;
    long long x0=rand()%x;
    long long y=x0;
    while(1)
    {
        i++;
        x0=(mult_mod(x0,x0,x)+c)%x;
        long long d=gcd(y-x0,x);
        if(d!=1&&d!=x) return d;
        if(y==x0) return x;
        if(i==k){y=x0;k+=k;}
    }
}
//对n进行素因子分解
void findfac(long long n)
{
    if(Miller_Rabin(n))//素数
    {
        mp[n]++;
        return;
    }
    long long p=n;
    while(p>=n)p=Pollard_rho(p,rand()%(n-1)+1);
    findfac(p);
    findfac(n/p);
}

int main()
{
    srand(time(NULL));
    long long n;
    while(scanf("%lld",&n)!=EOF)
    {
        if(n==1)
        {
            printf("1\n");
            continue;
        }
        mp.clear();
        tol=0;
        findfac(n);
        long long sum=1;
        for(it=mp.begin();it!=mp.end();it++){
            sum*=(1+it->second);
        }
        printf("%lld\n",sum);
    }
    return 0;
}

 

三.数学相关

3.1 扩展欧几里得算法

int exgcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    int r=exgcd(b,a%b,x,y);
    int t=x;
    x=y;
    y=t-a/b*y;
    return r;
}

 3.2 向量基本计算方法

#include<cstdio>
#include<cstring>
#include<cctype>
#include<cmath>
#include<algorithm>
#define eps 1e-8
using namespace std;

struct Point
{
    double x,y;
    Point(){}
    Point(double x,double y):x(x),y(y){}
    double operator *(const Point B)const{ return x*B.y-y*B.x; }
    Point operator -(const Point B)const{ return Point(x-B.x,y-B.y); }
    Point operator +(const Point B)const{ return Point(x+B.x,y+B.y); }
    Point operator *(const double B)const{ return Point(x*B,y*B); }
}A,B,C,D,L1,L2,P,Q,MA,MC;

int main()
{
    int T;scanf("%d",&T);
    for(;T--;)
    {
        scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&A.x,&A.y,&B.x,&B.y,&C.x,&C.y,&D.x,&D.y);
        if(A.y==B.y || C.y==D.y){ printf("0.00\n");continue; }
        if(A.y<B.y) swap(A,B);
        if(C.y<D.y) swap(C,D);
        double a=(C-A) * (D-A),b = (D-B) * (C-B);
        if(a*b<-eps){ printf("0.00\n"); continue;}
        P=(B-A) * (a / (a+b)) + A;
        if(P.y>C.y || P.y<D.y){ printf("0.00\n");continue; }
        if(A.y>C.y)
        {
            Q=B + (A-B) * ((C.x-B.x)/(A.x-B.x));
            if(Q.y>=C.y && A.y>=Q.y){ printf("0.00\n");continue;}
            MA=B + (A-B) * ((C.y-B.y)/(A.y-B.y));
            printf("%.2lf\n",fabs((MA-P) * (C-P) / 2));
        }
        else 
        {
            Q=D + (C-D) * ((A.x-D.x)/(C.x-D.x));
            if(Q.y>=A.y && C.y>=Q.y){ printf("0.00\n");continue; }
            MC=D+(C-D) * ((A.y-D.y) / (C.y-D.y));
            printf("%.2lf\n",fabs((MC-P) * (A-P) / 2) );
        }
    }
}

//https://blog.csdn.net/qq_16657927/article/details/79942140
/* 
    |16/11/06ztx| 
*/  
  
struct node {    
    double x; // 横坐标    
    double y; // 纵坐标    
};    
  
typedef node Vector;  
  
Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }    
Vector operator - (Point A, Point B) { return Vector(A.x - B.y, A.y - B.y); }    
Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); }    
Vector operator / (Vector A, double p) { return Vector(A.x / p, A.y*p); }    
  
double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; } // 向量点乘    
double Length(Vector A) { return sqrt(Dot(A, A)); }  // 向量模长    
double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); }  // 向量之间夹角    
  
double Cross(Vector A, Vector B) { // 叉积计算 公式    
    return A.x*B.y - A.y*B.x;    
}    
  
Vector Rotate(Vector A, double rad) // 向量旋转 公式  {    
    return Vector(A.x*cos(rad) - A.y*sin(rad), A.x*sin(rad) + A.y*cos(rad));    
}    
  
Point getLineIntersection(Point P, Vector v, Point Q, Vector w) { // 两直线交点t1 t2计算公式     
    Vector u = P - Q;     
    double t = Cross(w, u) / Cross(v, w);  // 求得是横坐标    
    return P + v*t;  // 返回一个点    
}    

3.3 求多边形面积

/* 
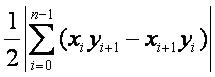
    |16/11/06ztx| 
*/  
  
node G[maxn];    
int n;    
  
double Cross(node a, node b) { // 叉积计算    
    return a.x*b.y - a.y*b.x;    
}    
  
  
int main()    
{    
    while (scanf("%d", &n) != EOF && n) {    
        for (int i = 0; i < n; i++)     
            scanf("%lf %lf", &G[i].x, &G[i].y);    
        double sum = 0;    
        G[n].x = G[0].x;    
        G[n].y = G[0].y;    
        for (int i = 0; i < n; i++) {     
                sum += Cross(G[i], G[i + 1]);    
        }    
        // 或者    
            //for (int i = 0; i < n; i++) {    
                //sum += fun(G[i], G[（i + 1）% n]);    
            //}    
        sum = sum / 2.0;    
        printf("%.1f\n", sum);    
    }    
    system("pause");    
    return 0;    
}  

3.4 判断直线相交

/*
    |16/11/06ztx|
*/

node P[35][105];     

double Cross_Prouct(node A,node B,node C) {     //  计算BA叉乘CA     
    return (B.x-A.x)*(C.y-A.y)-(B.y-A.y)*(C.x-A.x);      
}      
bool Intersect(node A,node B,node C,node D)  {  //  通过叉乘判断线段是否相交；           
    if(min(A.x,B.x)<=max(C.x,D.x)&&         //  快速排斥实验；      
       min(C.x,D.x)<=max(A.x,B.x)&&      
       min(A.y,B.y)<=max(C.y,D.y)&&      
       min(C.y,D.y)<=max(A.y,B.y)&&      
       Cross_Prouct(A,B,C)*Cross_Prouct(A,B,D)<0&&      //  跨立实验；      
       Cross_Prouct(C,D,A)*Cross_Prouct(C,D,B)<0)       //  叉乘异号表示在两侧；      
       return true;      
    else return false;      
}    

 3.5 凸包

/*
向量叉积判断多边形凹凸

       对于连续的三个点p0,p1,p2，另向量a=p1-p0，b=p2-p1若是凸多边形，那么b相对于a一定是向逆时针方向

旋转的。

 判断两向量的旋转方向，可以使用向量的叉积 a×b ＝ x1×y2 － x2×y1

  a×b > 0 b在a的逆时针方向
  a×b = 0 b平行于a（共线）
  a×b < 0 b在a的顺时针方向

要注意的是，对于最后一个点pn，还要和起始的两个点p0,p1判断一次。
*/
 

#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#define eps 1e-8
#define MAXN 110
using namespace std;
struct Point
{
    double x, y;
    Point(){}
    Point(double X, double Y){
        x = X; y = Y;
    }
};
Point P[MAXN];
int dcmp(double x)
{
    if(fabs(x) < eps)
        return 0;
    else
        return x < 0 ? -1 : 1;
}
Point operator - (Point A, Point B){
    return Point(A.x-B.x, A.y-B.y);
}
Point operator + (Point A, Point B){
    return Point(A.x+B.x, A.y+B.y);
}
Point operator * (Point A, double p){
    return Point(A.x*p, A.y*p);;
}
double Cross(Point A, Point B){
    return A.x*B.y - A.y*B.x;
}
double Dot(Point A, Point B){
    return A.x*B.x + A.y*B.y;
}
double Dis(Point A, Point B){
    return sqrt((A.x-B.x)*(A.x-B.x) + (A.y-B.y)*(A.y-B.y));
}
bool operator == (Point A, Point B){
    return dcmp(A.x-B.x) == 0 && dcmp(A.y-B.y) == 0;
}
bool cmp(Point A, Point B)//按极角升序排序，若角度相等距离小的在前面
{
    double temp = Cross(A-P[0], B-P[0]);
    if(dcmp(temp) > 0) return true;
    if(dcmp(temp) == 0 && dcmp(Dis(P[0], A) - Dis(P[0], B)) < 0) return true;
    return false;
}
int Stack[MAXN], top;//下标从0开始计数到top
void input(int n)
{
    scanf("%lf%lf", &P[0].x, &P[0].y);
    double xx = P[0].x, yy = P[0].y;
    int id = 0;//找到y坐标最小的点，若有多个选择x坐标最小的记录下标
    for(int i = 1; i < n; i++)
    {
        scanf("%lf%lf", &P[i].x, &P[i].y);
        if(P[i].y < yy || (P[i].y == yy && P[i].x < xx))
        {
            xx = P[i].x;
            yy = P[i].y;
            id = i;
        }
    }
    Point T;
    T = P[0]; P[0] = P[id]; P[id] = T;
    sort(P+1, P+n, cmp);//极角排序
}
void Graham(int n)
{
    if(n == 1){ top = 0; Stack[0] = 0;}
    else if(n == 2)
    {
        top = 1;
        Stack[0] = 0;
        Stack[1] = 1;
    }
    else
    {
        for(int i = 0; i <= 1; i++)
            Stack[i] = i;
        top = 1;
        for(int i = 2; i < n; i++)
        {   //如果和上一条边成左旋关系，压栈继续；反之一直弹栈直到和栈顶两点的边成左转关系，压栈继续。
            while(top > 0 && dcmp(Cross(P[Stack[top]]-P[Stack[top-1]], P[i]-P[Stack[top-1]])) <= 0) top--;
            top++;
            Stack[top] = i;
        }
    }
}
int main()
{
    int n;
    input(n);
    Graham(n);
    return 0;
}

3.6 计算几何模板

#include<iostream>
#include<cmath>
#include<cstdio>
#include<algorithm>
#define INF 1E200
using namespace std;
const double PI  = 3.14159265;//||acos(-1)
const double eps=0.0000000001;
struct Point //点
{
    double x,y;
    Point (double a=0,double b=0):x(a),y(b) {}
};
struct Line_segment //线段
{
    Point s,e;
    Line_segment() {}
    Line_segment(Point a,Point b):s(a),e(b) {}
};
struct Line //直线
{
    double A,B,C;
    Line(double A=1,double B=-1,double C=0):A(A),B(B),C(C) {}
};
inline double Max(double a,double b)
{
    return a>b?a:b;
}
inline double Min(double a,double b)
{
    return a<b?a:b;
}
 
//计算几何 开始!
double Dist(Point a,Point b) //1.两点之间距离
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
bool equal_Point(Point a,Point b) //2.判断两点是否重合
{
    return fabs(a.x-b.x)<eps&&fabs(a.y-b.y)<eps;
}
double multiply(Point sp,Point  ep,Point op) //3.叉积//要判断点在直线哪一侧时,sp,ep为线段或者直线上两点,op为判断的点
{
    /******************************************************************************
    r=multiply(sp,ep,op),得到(sp-op) 和 ( ep-op)的叉积
    r>0; ep在矢量op sp的逆时针方向//点在直线右边
    r=0;op sp ep 三点共线；
    r<0;ep在矢量op sp的顺时针方向//点在直线左边
    *******************************************************************************/
    return((sp.x-op.x)*(ep.y-op.y)-(ep.x-op.x)*(sp.y-op.y));
}
double dotmultiply(Point p1,Point p2,Point p0) //4.点积
{
    /******************************************************************************
    r=dotmultiply(p1,p2,op),得到矢量(p1-op)和(p2-op)的点积,如果两个矢量都非零矢量
    r<0:两矢量夹角为钝角;
    r=0:两矢量夹角为直角;
    r>0:两矢量夹角为锐角;
    *******************************************************************************/
    return (p1.x-p0.x)*(p2.x-p0.x)+(p1.y-p0.y)*(p2.y-p0.y);
}
bool online(Line_segment l,Point p)//5.判断点p是否在线段l上 +3
{
    /******************************************************************************
    判断点p是否在线段l上
    条件：(p在线段l所在的直线上) && (点p在以线段l为对角线的矩形内)
    *******************************************************************************/
    return( (multiply(l.e,p,l.s)==0) &&( ( (p.x-l.s.x)*(p.x-l.e.x)<=0 )&&( (p.y-l.s.y)*(p.y-l.e.y)<=0 ) ) );
}
Point Rotate(Point o,double alpha,Point p) // 6.返回点p以点o为圆心逆时针旋转alpha(单位：弧度)后所在的位置
{
    Point tp;
    p.x-=o.x;
    p.y-=o.y;
    tp.x=p.x*cos(alpha)-p.y*sin(alpha)+o.x;
    tp.y=p.y*cos(alpha)+p.x*sin(alpha)+o.y;
    return tp;
}
double angle(Point o,Point s,Point e) //7.返回顶角在o点，起始边为os，终止边为oe的夹角(单位：弧度)
{
    /******************************************************************************
       返回顶角在o点，起始边为os，终止边为oe的夹角(单位：弧度)
    角度小于pi，返回正值
    角度大于pi，返回负值
    可以用于求线段之间的夹角
    原理：
    r = dotmultiply(s,e,o) / (dist(o,s)*dist(o,e))
    r'= multiply(s,e,o)
    r >= 1 angle = 0;
    r <= -1 angle = -PI
    -1<r<1 && r'>0 angle = arccos(r)
    -1<r<1 && r'<=0 angle = -arccos(r)
    ********************************************************************************/
    double cosfi,fi,norm;
    double dsx = s.x - o.x;
    double dsy = s.y - o.y;
    double dex = e.x - o.x;
    double dey = e.y - o.y;
    cosfi=dsx*dex+dsy*dey;
    norm=(dsx*dsx+dsy*dsy)*(dex*dex+dey*dey);
    cosfi /= sqrt( norm );
    if (cosfi >=  1.0 ) return 0;
    if (cosfi <= -1.0 ) return -3.1415926;
    fi=acos(cosfi);
    if (dsx*dey-dsy*dex>0) return fi;      // 说明矢量os 在矢量 oe的顺时针方向
    return -fi;
}
double relation(Point p,Line_segment l) //8.判断点与线段的关系
{
    /******************************************************************************
    判断点与线段的关系,用途很广泛
    本函数是根据下面的公式写的，P是点C到线段AB所在直线的垂足
            AC dot AB
    r =     ---------
             ||AB||^2
         (Cx-Ax)(Bx-Ax) + (Cy-Ay)(By-Ay)
      = -------------------------------
                      L^2
    r has the following meaning:
    r=0      P = A
    r=1      P = B
    r<0   P is on the backward extension of AB
    r>1      P is on the forward extension of AB
    0<r<1  P is interior to AB
    ********************************************************************************/
    Line_segment tl;
    tl.s=l.s;
    tl.e=p;
    return dotmultiply(tl.e,l.e,l.s)/(Dist(l.s,l.e)*Dist(l.s,l.e));
}
Point perpendicular(Point p,Line_segment l) //9.求点C到线段AB所在直线的垂足 P
{
    /******************************************************************************
       求点C到线段AB所在直线的垂足 P
       *******************************************************************************/
    double r=relation(p,l);
    Point tp;
    tp.x=l.s.x+r*(l.e.x-l.s.x);
    tp.y=l.s.y+r*(l.e.y-l.s.y);
    return tp;
}
double ptolinesegdist(Point p,Line_segment l,Point &np) //10.求点p到线段l的最短距离,并返回线段上距该点最近的点np
{
    /******************************************************************************
       求点p到线段l的最短距离,并返回线段上距该点最近的点np
    注意：np是线段l上到点p最近的点，不一定是垂足
    *******************************************************************************/
    double r=relation(p,l);
    if(r<0)
    {
        np=l.s;
        return Dist(p,l.s);
    }
    if(r>1)
    {
        np=l.e;
        return Dist(p,l.e);
    }
    np=perpendicular(p,l);
    return Dist(p,np);
}
double ptoldist(Point p,Line_segment l) // 11.求点p到线段l所在直线的距离,请注意本函数与上个函数的区别
{
    return abs(multiply(p,l.e,l.s))/Dist(l.s,l.e);
}
double ptopointset(int vcount,Point pointset[],Point p,Point &q) //12.计算点到折线集的最近距离,并返回最近点.
{
    /******************************************************************************
     计算点到折线集的最近距离,并返回最近点.
    注意：调用的是ptolineseg()函数
    *******************************************************************************/
    int i;
    double cd=double(INF),td;
    Line_segment l;
    Point tq,cq;
    for(i=0; i<vcount-1; i++)
    {
        l.s=pointset[i];
        l.e=pointset[i+1];
        td=ptolinesegdist(p,l,tq);
        if(td<cd)
        {
            cd=td;
            cq=tq;
        }
    }
    q=cq;
    return cd;
}
bool CircleInsidePolygon(int vcount,Point center,double radius,Point polygon[]) //13.判断圆是否在多边形内.ptolineseg()函数的应用
{
    Point q;
    double d;
    q.x=0;
    q.y=0;
    d=ptopointset(vcount,polygon,center,q);
    if(d>radius||fabs(d-radius)<eps)
        return true;//若不考虑相切的情况,去掉 fabs(d-radius)<eps
 
    else
        return false;
}
double cosine(Line_segment l1,Line_segment l2)   //14.返回两个 矢量 l1和l2的夹角的余弦
{
    /******************************************************************************
    返回两个矢量l1和l2的夹角的余弦(-1 --- 1)注意：如果想从余弦求夹角的话，注意反余弦函数的定义域是从 0到pi
    *******************************************************************************/
    return (((l1.e.x-l1.s.x)*(l2.e.x-l2.s.x) +(l1.e.y-l1.s.y)*(l2.e.y-l2.s.y))/(Dist(l1.e,l1.s)*Dist(l2.e,l2.s)));
}
double lsangle(Line_segment l1,Line_segment l2)  // 15.返回线段l1与l2之间的夹角 单位:弧度 范围(-pi，pi)
{
    Point o,s,e;
    o.x=o.y=0;
    s.x=l1.e.x-l1.s.x;
    s.y=l1.e.y-l1.s.y;
    e.x=l2.e.x-l2.s.x;
    e.y=l2.e.y-l2.s.y;
    return angle(o,s,e);
}
bool intersect(Line_segment u,Line_segment v) // 16.如果线段u和v相交(包括相交在端点处)时,返回true
{
    /******************************************************************************
    如果线段u和v相交(包括相交在端点处)时,返回true
    判断P1P2跨立Q1Q2的依据是: ( P1 - Q1 ) x ( Q2 - Q1 ) x ( Q2 - Q1 ) x ( P2 - Q1 ) >= 0
    判断Q1Q2跨立P1P2的依据是: ( Q1 - P1 ) x ( P2 -  P1 ) x ( P2 - P1 ) x ( Q2 - P1 ) >= 0
    *******************************************************************************/
    return((Max(u.s.x,u.e.x)>=Min(v.s.x,v.e.x))&&                     //排斥实验
           (Max(v.s.x,v.e.x)>=Min(u.s.x,u.e.x))&&
           (Max(u.s.y,u.e.y)>=Min(v.s.y,v.e.y))&&
           (Max(v.s.y,v.e.y)>=Min(u.s.y,u.e.y))&&
           (multiply(v.s,u.e,u.s)*multiply(u.e,v.e,u.s)>=0)&&         //跨立实验
           (multiply(u.s,v.e,v.s)*multiply(v.e,u.e,v.s)>=0));
}
bool intersect_A(Line_segment u,Line_segment v) // 17.(线段u和v相交)&&(交点不是端点)时返回true
{
    return ((intersect(u,v))&&
            (!online(u,v.s))&&
            (!online(u,v.e))&&
            (!online(v,u.e))&&
            (!online(v,u.s)));
}
bool intersect_l(Line_segment u,Line_segment v)// 18.线段v所在直线与线段u相交时返回true
{
    /******************************************************************************
    线段v所在直线与线段u相交时返回true;方法;判断线段u是否跨立线段v
    *******************************************************************************/
    return multiply(u.s,v.e,v.s)*multiply(v.e,u.e,v.s)>=0;
}
Line makeline(Point p1,Point p2)   // 19.根据已知两点坐标，求过这两点的直线解析方程
{
    /******************************************************************************
    根据已知两点坐标，求过这两点的直线解析方程Ax+By+C=0 (A>=0)
    *******************************************************************************/
    Line tl;
    int sign = 1;
    tl.A=p2.y-p1.y;
    if(tl.A<0)
    {
        sign = -1;
        tl.A=sign*tl.A;
    }
    tl.B=sign*(p1.x-p2.x);
    tl.C=sign*(p1.y*p2.x-p1.x*p2.y);
    return tl;
}
double slope(Line l)   // 20.根据直线解析方程返回直线的斜率k,  水平线返回 0, 竖直线返回 1e200
{
    if(abs(l.A) < 1e-20)
        return 0;
    if(abs(l.B) < 1e-20)
        return INF;
    return -(l.A/l.B);
}
double alpha(Line l)   //21. 返回直线的倾斜角 alpha ( 0 - pi)
{
    if(abs(l.A)< eps)
        return 0;
    if(abs(l.B)< eps)
        return PI/2;
    double k=slope(l);
    if(k>0)
        return atan(k);
    else
        return PI+atan(k);
}
Point symmetry(Line l,Point p) //22. 求点p关于直线l的对称点
{
    Point tp;
    tp.x=((l.B*l.B-l.A*l.A)*p.x-2*l.A*l.B*p.y-2*l.A*l.C)/(l.A*l.A+l.B*l.B);
    tp.y=((l.A*l.A-l.B*l.B)*p.y-2*l.A*l.B*p.x-2*l.B*l.C)/(l.A*l.A+l.B*l.B);
    return tp;
}
bool lineintersect(Line l1,Line l2,Point &p) // 23.两直线相交返回true并返回交点p,不相交则返回false
{
    double d=l1.A*l2.B-l2.A*l1.B;
    if(abs(d)<eps) // 不相交
        return false;
    p.x = (l2.C*l1.B-l1.C*l2.B)/d;
    p.y = (l2.A*l1.C-l1.A*l2.C)/d;
    return true;
}
bool intersection(Line_segment l1,Line_segment l2,Point &inter)   // 24.如果线段l1和l2相交，返回true且交点由(inter)返回，否则返回false
{
    Line ll1,ll2;
    ll1=makeline(l1.s,l1.e);
    ll2=makeline(l2.s,l2.e);
    if(intersect(l1,l2)==1)
    {
        lineintersect(ll1,ll2,inter);
        return true;
    }
    else
        return false;
}
/*******************************************************************************/
bool point_in_circle(Point o,double r,Point p)   //25. 返回值:点p在圆内(包括边界)时,返回true
{
    /******************************************************************************
    参数o为圆心,r为半径,p为判断的点
    返回值:点p在圆内(包括边界)时,返回true
    *******************************************************************************/
    double d2=(p.x-o.x)*(p.x-o.x)+(p.y-o.y)*(p.y-o.y);
    double r2=r*r;
    return d2<r2||abs(d2-r2)<eps;
}
 
bool cocircle(Point p1,Point p2,Point p3,Point &q,double &r) //26.三点确定一个圆,不能构成圆返回false
{
    /******************************************************************************
    用 途 :求不共线的三点确定一个圆
    输 入 :三个点p1,p2,p3
    返回值 :如果三点共线，返回false；反之，返回true。圆心由q返回，半径由r返回
    *******************************************************************************/
    double x12=p2.x-p1.x;
    double y12=p2.y-p1.y;
    double x13=p3.x-p1.x;
    double y13=p3.y-p1.y;
    double z2=x12*(p1.x+p2.x)+y12*(p1.y+p2.y);
    double z3=x13*(p1.x+p3.x)+y13*(p1.y+p3.y);
    double d=2.0*(x12*(p3.y-p2.y)-y12*(p3.x-p2.x));
    if(abs(d)<eps) //共线，圆不存在
        return false;
    q.x=(y13*z2-y12*z3)/d;
    q.y=(x12*z3-x13*z2)/d;
    r=Dist(p1,q);
    return true;
}
int CircleRelation(Point p1, double r1, Point p2, double r2) //27.两圆位置关系
{
    /******************************************************************************
    相离:return 1
    外切:return 2
    相交:return 3
    内切:return 4
    内含:return 5
    *******************************************************************************/
    double d = sqrt( (p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y) );
    if( fabs(d-r1-r2) < eps ) // 必须保证前两个if先被判定！
        return 2;
    if( fabs(d-fabs(r1-r2)) < eps )
        return 4;
    if( d > r1+r2 )
        return 1;
    if( d < fabs(r1-r2) )
        return 5;
    if( fabs(r1-r2) < d && d < r1+r2 )
        return 3;
    return 0; // indicate an error!未知错误
}
double P2planeDist(double x, double y, double z, double a, double b, double c, double d) //28.空间 点到平面距离
{
    /******************************************************************************
    空间点到平面的距离,平面用一般式表示ax+by+cz+d=0
    *******************************************************************************/
    return fabs(a*x+b*y+c*z+d) / sqrt(a*a+b*b+c*c);
}
bool SameSide(Point p1, Point p2, Line line) //29.点在直线同侧返回true
{
    return (line.A * p1.x + line.B * p1.y + line.C) *
           (line.A * p2.x + line.B * p2.y + line.C) > 0;
}
void  c2point(Point p1,double r1,Point p2,double r2,Point &rp1,Point &rp2) //30.两个圆(已判断为相交或相切)的交点rp1,rp2
{
    double a,b,r;
    a=p2.x-p1.x;
    b=p2.y-p1.y;
    r=(a*a+b*b+r1*r1-r2*r2)/2;
    if(a==0&&b!=0)
    {
        rp1.y=rp2.y=r/b;
        rp1.x=sqrt(r1*r1-rp1.y*rp1.y);
        rp2.x=-rp1.x;
    }
    else if(a!=0&&b==0)
    {
        rp1.x=rp2.x=r/a;
        rp1.y=sqrt(r1*r1-rp1.x*rp2.x);
        rp2.y=-rp1.y;
    }
    else if(a!=0&&b!=0)
    {
        double delta;
        delta=b*b*r*r-(a*a+b*b)*(r*r-r1*r1*a*a);
        rp1.y=(b*r+sqrt(delta))/(a*a+b*b);
        rp2.y=(b*r-sqrt(delta))/(a*a+b*b);
        rp1.x=(r-b*rp1.y)/a;
        rp2.x=(r-b*rp2.y)/a;
    }
    rp1.x+=p1.x;
    rp1.y+=p1.y;
    rp2.x+=p1.x;
    rp2.y+=p1.y;
}
double c2area(Point p1,double r1,Point p2,double r2) //31.两相交圆公共面积 +30
{
    double TEMP;
    Point rp1,rp2,rp;
    c2point(p1,r1,p2,r2,rp1,rp2);
    if(r1>r2) //保证r2>r1
    {
        rp=p1;
        p1=p2;
        p2=rp;
        TEMP=r1;
        r1=r2;
        r2=TEMP;
    }
    double a,b,rr;
    a=p1.x-p2.x;
    b=p1.y-p2.y;
    rr=sqrt(a*a+b*b);
    double dx1,dy1,dx2,dy2;
    double sita1,sita2;
    dx1=rp1.x-p1.x;
    dy1=rp1.y-p1.y;
    dx2=rp2.x-p1.x;
    dy2=rp2.y-p1.y;
    sita1=acos((dx1*dx2+dy1*dy2)/r1/r1);
    dx1=rp1.x-p2.x;
    dy1=rp1.y-p2.y;
    dx2=rp2.x-p2.x;
    dy2=rp2.y-p2.y;
    sita2=acos((dx1*dx2+dy1*dy2)/r2/r2);
    double s=0;
    if(rr<r2)//相交弧为优弧
        s=r1*r1*(PI-sita1/2+sin(sita1)/2)+r2*r2*(sita2-sin(sita2))/2;
    else//相交弧为劣弧
        s=(r1*r1*(sita1-sin(sita1))+r2*r2*(sita2-sin(sita2)))/2;
 
 
    return s;
}
 
int clpoint(Point p,double r,double a,double b,double c,Point &rp1,Point &rp2) //32.圆和直线(ax+by+c=0,a>=0)关系
{
    /******************************************************************************
    相离 return 0
    相切 return 1
    相交 return 2
    *******************************************************************************/
    int res=0;
    c=c+a*p.x+b*p.y;
    double tmp;
    if(a==0&&b!=0)
    {
        tmp=-c/b;
        if(r*r<tmp*tmp)
            res=0;
        else if(r*r==tmp*tmp)
        {
            res=1;
            rp1.y=tmp;
            rp1.x=0;
        }
        else
        {
            res=2;
            rp1.y=rp2.y=tmp;
            rp1.x=sqrt(r*r-tmp*tmp);
            rp2.x=-rp1.x;
        }
    }
    else if(a!=0&&b==0)
    {
        tmp=-c/a;
        if(r*r<tmp*tmp)
            res=0;
        else if(r*r==tmp*tmp)
        {
            res=1;
            rp1.x=tmp;
            rp1.y=0;
        }
        else
        {
            res=2;
            rp1.x=rp2.x=tmp;
            rp1.y=sqrt(r*r-tmp*tmp);
            rp2.y=-rp1.y;
        }
    }
    else if(a!=0&&b!=0)
    {
        double delta;
        delta=b*b*c*c-(a*a+b*b)*(c*c-a*a*r*r);
        if(delta<0)
            res=0;
        else if(delta==0)
        {
            res=1;
            rp1.y=-b*c/(a*a+b*b);
            rp1.x=(-c-b*rp1.y)/a;
        }
        else
        {
            res=2;
            rp1.y=(-b*c+sqrt(delta))/(a*a+b*b);
            rp2.y=(-b*c-sqrt(delta))/(a*a+b*b);
            rp1.x=(-c-b*rp1.y)/a;
            rp2.x=(-c-b*rp2.y)/a;
        }
    }
    rp1.x+=p.x;
    rp1.y+=p.y;
    rp2.x+=p.x;
    rp2.y+=p.y;
    return res;
}
void incircle(Point p1,Point p2,Point p3,Point &rp,double &r) // 33.三角形内切圆
{
    double dx31,dy31,dx21,dy21,d31,d21,a1,b1,c1;
    dx31=p3.x-p1.x;
    dy31=p3.y-p1.y;
    dx21=p2.x-p1.x;
    dy21=p2.y-p1.y;
    d31=sqrt(dx31*dx31+dy31*dy31);
    d21=sqrt(dx21*dx21+dy21*dy21);
    a1=dx31*d21-dx21*d31;
    b1=dy31*d21-dy21*d31;
    c1=a1*p1.x+b1*p1.y;
    double dx32,dy32,dx12,dy12,d32,d12,a2,b2,c2;
    dx32=p3.x-p2.x;
    dy32=p3.y-p2.y;
    dx12=-dx21;
    dy12=-dy21;
    d32=sqrt(dx32*dx32+dy32*dy32);
    d12=d21;
    a2=dx12*d32-dx32*d12;
    b2=dy12*d32-dy32*d12;
    c2=a2*p2.x+b2*p2.y;
    rp.x=(c1*b2-c2*b1)/(a1*b2-a2*b1);
    rp.y=(c2*a1-c1*a2)/(a1*b2-a2*b1);
    r=fabs(dy21*rp.x-dx21*rp.y+dx21*p1.y-dy21*p1.x)/d21;
}
 
void cutpoint(Point p,double r,Point sp,Point &rp1,Point &rp2) //34.过圆外一点的直线与圆的两个切点(p为圆心,r为圆半径,点sp为圆外一点)
{
    Point p2;
    p2.x=(p.x+sp.x)/2;
    p2.y=(p.y+sp.y)/2;
    double dx2,dy2,r2;
    dx2=p2.x-p.x;
    dy2=p2.y-p.y;
    r2=sqrt(dx2*dx2+dy2*dy2);
    c2point(p,r,p2,r2,rp1,rp2);
}
 
void DoneSq(Point a, Point c,Point& b,Point &d)//35.已知正方形对角线上两顶点(a和c),求另两点(b和d);
{
    double x,y,mx,my;
    mx = (a.x+c.x)/2.0;
    my = (a.y+c.y)/2.0;
    x = a.x - mx;
    y = a.y - my;
    b.x = -y + mx;
    b.y = x + my;
    x = c.x - mx;
    y = c.y - my;
    d.x = - y + mx;
    d.y = x + my;
}
void makeline2(Line& L,const Point& a,const double& k)// 36. 根据一点坐标及其斜率k(已证实存在),求这条直线的解析方程
{
    L.A=k;
    L.B=-1;
    L.C=a.y-k*a.x;
}
 
void min_cover_circle(Point *p,int n,Point &c,double &r)// 37.随机增量算法求最小覆盖圆 (点/点的个数/圆心/半径)
{
    random_shuffle(p,p+n);
    c=p[0];
    r=0;
    for(int i=1; i<n; i++)
    {
        if(Dist(p[i],c)>r+eps)
        {
            c=p[i];
            r=0;
            for(int j=0; j<i; j++)
                if(Dist(p[j],c)>r+eps)
                {
                    c.x=(p[i].x+p[j].x)/2;
                    c.y=(p[i].y+p[j].y)/2;
                    r=Dist(p[j],c);
                    for(int k=0; k<j; k++)
                        if(Dist(p[k],c)>r+eps)
                        {
                            cocircle(p[i],p[j],p[k],c,r);
                        }
                }
        }
    }
}
bool InsideConvexPolygon(int vcount,Point polygon[],Point q) // 38.判断点q是否在凸多边形内//多边形顶点<=2时返回0
{
    if(vcount<3) return 0;
    Point p;
    Line_segment l;
    int i;
    p.x=0;
    p.y=0;
    for(i=0; i<vcount; i++) // 寻找一个肯定在多边形polygon内的点p;多边形顶点平均值
    {
        p.x+=polygon[i].x;
        p.y+=polygon[i].y;
    }
    p.x /= vcount;
    p.y /= vcount;
 
    for(i=0; i<vcount; i++)
    {
        l.s=polygon[i];
        l.e=polygon[(i+1)%vcount];
        if(multiply(p,l.e,l.s)*multiply(q,l.e,l.s)<0) /* 点p和点q在边l的两侧，说明点q肯定在多边形外 */
            break;
    }
    return (i==vcount);
}
 
double Getarea(int n,Point top[])// 39.计算顶点已按逆时针或顺时针排好的 多边形面积,
{
    Point p=top[0];
    double s=0;
    for(int i=0; i<n-1; i++)
    {
        s+=top[i].x*top[i+1].y-top[i].y*top[i+1].x;
    }
    s+=top[n-1].x*top[0].y-top[n-1].y*top[0].x;
    return fabs(s/2);
}
bool cmp1(Point a,Point b)//凸包排序方法
{
    if(a.x == b.x)
        return a.y < b.y;
    return a.x < b.x;
}
 
int graham(Point pnt[],int n,Point res[])//40.求凸包,pnt为点集，n为点的个数，res为凸包上的点，返回值为凸包点的个数
{
    sort(pnt,pnt+n,cmp1);
    int m=0, i, k;
    for(i = 0; i < n; i++)
    {
        while(m>1 && multiply(res[m-1],pnt[i],res[m-2])<=0)
            m--;
        res[m++]=pnt[i];
    }
    k = m;
    for(i = n-2; i >= 0; i--)
    {
        while(m>k && multiply(res[m-1],pnt[i],res[m-2])<=0)
            m--;
        res[m++]=pnt[i];
    }
    if(n > 1)//起始点重复。
        m--;
    return m;
}
double area1(Point c,double r,int n)//41.圆与n边形相交面积 c为圆心,r为半径 数组P为含n个点的数组
{
    Point a,b;
    double A,B,C,x,y,tS,Ans=0;
    for(int i=0; i<n; i++)
    {
        a=P[i];    //数组P为多边形顶点数组
        b=P[(i+1)%n];
        A=Dist(b,c);
        B=Dist(a,c);
        C=Dist(b,a);
        if(A<r&&B<r)
            Ans+= multiply(a,b,c)/2;
        else if(A<r&&B>=r)
        {
            x=(dotmultiply(a,c,b)+sqrt(r*r*C*C-multiply(a,c,b)*multiply(a,c,b)))/C;
            tS=multiply(a,b,c)/2;
            Ans+= asin(tS*(1-x/C)*2/r/B*(1-eps))*r*r/2+tS*x/C;
        }
        else if(A>=r&&B<r)
        {
            y=(dotmultiply(b,c,a)+sqrt(r*r*C*C-multiply(b,c,a)*multiply(b,c,a)))/C;
            tS=multiply(a,b,c)/2;
            Ans+= asin(tS*(1-y/C)*2/r/A*(1-eps))*r*r/2+tS*y/C;
        }
        else if(fabs(multiply(a,b,c))>=r*C||dotmultiply(b,c,a)<=0||dotmultiply(a,c,b)<=0)
        {
            if(dotmultiply(a,b,c)<0)
                if(multiply(a,b,c)<0)
                    Ans+= (-acos(-1.0)-asin(multiply(a,b,c)/A/B*(1-eps)))*r*r/2;
                else Ans+= (acos(-1.0)-asin(multiply(a,b,c)/A/B*(1-eps)))*r*r/2;
            else Ans+= asin(multiply(a,b,c)/A/B*(1-eps))*r*r/2;
        }
        else
        {
            x=(dotmultiply(a,c,b)+sqrt(r*r*C*C-multiply(a,c,b)*multiply(a,c,b)))/C;
            y=(dotmultiply(b,c,a)+sqrt(r*r*C*C-multiply(b,c,a)*multiply(b,c,a)))/C;
            tS=multiply(a,b,c)/2;
            Ans+= (asin(tS*(1-x/C)*2/r/B*(1-eps))+asin(tS*(1-y/C)*2/r/A*(1-eps)))*r*r/2+tS*((y+x)/C-1);
        }
    }
    return Ans;
}
int main()
{
    double a,b,c,d;
    Point m(1,1),n(2,2);
    Line_segment w(m,n);
    while(~scanf("%lf %lf",&a,&b))
    {
        Point A(a,b);
        if(online(w,A)) printf("yes\n");
        else printf("n0\n");
    }
    return 0;
}

 3.7 孙子定理 中国剩余定理

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

typedef long long ll;
ll a[100005],r[100005];
int n;

ll exgcd(ll a,ll b,ll &x,ll &y){
    if(b==0) return x=1,y=0,a;
    ll tmp=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return tmp;
}

ll solve(){
    ll M=a[1],R=r[1],x,y,d;
    for(int i=2;i<=n;i++){
        d=exgcd(M,a[i],x,y);
        if((R-r[i])%d!=0) return -1;
        x=(R-r[i])/d*x%a[i];
        R-=x*M;
        M=M/d*a[i];
        R%=M;
    }
    return (R%M+M)%M;
}

int main(){
    while(~scanf("%d",&n)){
        for(int i=1;i<=n;i++)scanf("%lld%lld",&a[i],&r[i]);
        printf("%lld\n",solve());
    }
    return 0;
}

 3.8 辛普森积分

double simpson(double a,double b)
{
    double c = a + (b-a)/2;
    return (F(a) + 4*F(c) + F(b))*(b-a)/6;
}
double asr(double a,double b,double eps,double A)
{
    double c = a + (b-a)/2;
    double L = simpson(a,c), R = simpson(c,b);
    if(fabs(L + R - A) <= 15*eps)return L + R + (L + R - A)/15.0;
    return asr(a,c,eps/2,L) + asr(c,b,eps/2,R);
}
double asr(double a,double b,double eps)
{
    return asr(a,b,eps,simpson(a,b));
}

 3.9 高斯消元求解线性方程组

 #include<stdio.h>
    #include<algorithm>
    #include<iostream>
    #include<string.h>
    #include<math.h>
    using namespace std;
    const int MAXN=50;
    int a[MAXN][MAXN];//增广矩阵
    int x[MAXN];//解集
    bool free_x[MAXN];//标记是否是不确定的变元
    int gcd(int a,int b){
        if(b == 0) return a; else return gcd(b,a%b);
    }
    inline int lcm(int a,int b){
        return a/gcd(a,b)*b;//先除后乘防溢出
    }
    // 高斯消元法解方程组(Gauss-Jordan elimination).(-2表示有浮点数解，但无整数解，
    //-1表示无解，0表示唯一解，大于0表示无穷解，并返回自由变元的个数)
    //有equ个方程，var个变元。增广矩阵行数为equ,分别为0到equ-1,列数为var+1,分别为0到var.
    int Gauss(int equ,int var){
        int i,j,k;
        int max_r;// 当前这列绝对值最大的行.
        int col;//当前处理的列
        int ta,tb;
        int LCM;
        int temp;
        int free_x_num;
        int free_index;

        for(int i=0;i<=var;i++){
            x[i]=0;
            free_x[i]=true;
        }

        //转换为阶梯阵.
        col=0; // 当前处理的列
        for(k = 0;k < equ && col < var;k++,col++){// 枚举当前处理的行.
        // 找到该col列元素绝对值最大的那行与第k行交换.(为了在除法时减小误差)
            max_r=k;
            for(i=k+1;i<equ;i++){
                if(abs(a[i][col])>abs(a[max_r][col])) max_r=i;
            }
            if(max_r!=k){// 与第k行交换.
                for(j=k;j<var+1;j++) swap(a[k][j],a[max_r][j]);
            }
            if(a[k][col]==0){// 说明该col列第k行以下全是0了，则处理当前行的下一列.
                k--;
                continue;
            }
            for(i=k+1;i<equ;i++){// 枚举要删去的行.
                if(a[i][col]!=0){
                    LCM = lcm(abs(a[i][col]),abs(a[k][col]));
                    ta = LCM/abs(a[i][col]);
                    tb = LCM/abs(a[k][col]);
                    if(a[i][col]*a[k][col]<0)tb=-tb;//异号的情况是相加
                    for(j=col;j<var+1;j++){
                        a[i][j] = a[i][j]*ta-a[k][j]*tb;
                    }
                }
            }
        }
        // 1. 无解的情况: 化简的增广阵中存在(0, 0, ..., a)这样的行(a != 0).
        for (i = k; i < equ; i++){ // 对于无穷解来说，如果要判断哪些是自由变元，那么初等行变换中的交换就会影响，则要记录交换.
            if (a[i][col] != 0) return -1;
        }
        // 2. 无穷解的情况: 在var * (var + 1)的增广阵中出现(0, 0, ..., 0)这样的行，即说明没有形成严格的上三角阵.
        // 且出现的行数即为自由变元的个数.
        if (k < var){
            return var - k; // 自由变元有var - k个.
        }
        // 3. 唯一解的情况: 在var * (var + 1)的增广阵中形成严格的上三角阵.
        // 计算出Xn-1, Xn-2 ... X0.
        for (i = var - 1; i >= 0; i--){
            temp = a[i][var];
            for (j = i + 1; j < var; j++){
                if (a[i][j] != 0) temp -= a[i][j] * x[j];
            }
            if (temp % a[i][i] != 0) return -2; // 说明有浮点数解，但无整数解.
            x[i] = temp / a[i][i];
        }
        return 0;
    }
    int main(void){
    //    freopen("in.txt", "r", stdin);
    //    freopen("out.txt","w",stdout);
        int i, j;
        int equ,var;
        while (scanf("%d %d", &equ, &var) != EOF){
            memset(a, 0, sizeof(a));
            for (i = 0; i < equ; i++){
                for (j = 0; j < var + 1; j++){
                    scanf("%d", &a[i][j]);
                }
            }
            int free_num = Gauss(equ,var);
            if (free_num == -1) printf("无解!\n");
            else if (free_num == -2) printf("有浮点数解，无整数解!\n");
            else if (free_num > 0){
                printf("无穷多解! 自由变元个数为%d\n", free_num);
                for (i = 0; i < var; i++){
                    if (free_x[i]) printf("x%d 是不确定的\n", i + 1);
                    else printf("x%d: %d\n", i + 1, x[i]);
                }
            }else{
                for (i = 0; i < var; i++){
                    printf("x%d: %d\n", i + 1, x[i]);
                }
            }
            printf("\n");
        }
        return 0;
    }

 3.10 整除分块

for(int l=1,r;l<=n;l=r+1)
{
    r=n/(n/l);
    ans+=(r-l+1)*(n/l);
}

 3.11 求莫比乌斯函数

/*莫比乌斯函数具有两个性质：
1.对于任意正整数nn，∑d|nμ(d)=[n=1]∑d|nμ(d)=[n=1]。（[n=1][n=1]表示只有当n=1n=1成立时，返回值为11；否则，值为00；(这个就是用μμ是容斥系数的性质可以证明)(PS:这一条性质是莫比乌斯反演中最常用的)
所有可以整除n的数的莫比乌斯函数之和等于0（特别的，n==1时等于1）。
2.对于任意正整数nn，∑d|nμ(d)d=ϕ(n)n∑d|nμ(d)d=ϕ(n)n。（这个性质很奇妙，它把欧拉函数和莫比乌斯函数结合起来，或许我之后写杜教筛的学习笔记时会去证明吧）
所有可以整除n的数d的莫比乌斯函数除以d的和等于 欧拉函数除以n的值
*/
void get_mu(int n)
{
    mu[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!vis[i]){prim[++cnt]=i;mu[i]=-1;}
        for(int j=1;j<=cnt&&prim[j]*i<=n;j++)
        {
            vis[prim[j]*i]=1;
            if(i%prim[j]==0)break;
            else mu[i*prim[j]]=-mu[i];
        }
    }
 

 3.12 杜教筛

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int maxn = 1700010;
int T, tot, prime[maxn], mu[maxn];
map<int, ll> ans_mu;

void sieve() {
    fill(prime, prime + maxn, 1);
    mu[1] = 1, tot = 0;
    for (int i = 2; i < maxn; i++) {
        if (prime[i]) {
            prime[++tot] = i, mu[i] = -1;
        }
        for (int j = 1; j <= tot && i * prime[j] < maxn; j++) {
            prime[i * prime[j]] = 0;
            if (i % prime[j] == 0) {
                mu[i * prime[j]] = 0; break;
            } else {
                mu[i * prime[j]] = -mu[i];
            }
        }
    }
    for (int i = 2; i < maxn; i++) mu[i] += mu[i - 1];
}

ll calc_mu(int x) {
    if (x < maxn) return mu[x];
    if (ans_mu.count(x)) return ans_mu[x];
    ll ans = 1;
    for (ll i = 2, j; i <= x; i = j + 1) {
        j = x / (x / i), ans -= (j - i + 1) * calc_mu(x / i);
    }
    return ans_mu[x] = ans;
}

ll calc_phi(int x) {
    ll ans = 0;
    for (ll i = 1, j; i <= x; i = j + 1) {
        j = x / (x / i), ans += (x / i) * (x / i) * (calc_mu(j) - calc_mu(i - 1));
    }
    return ((ans - 1) >> 1) + 1;
}

int main() {
    sieve();
    scanf("%d", &T);
    for (int i = 1, n; i <= T; i++) {
        scanf("%d", &n);
        printf("%lld %lld\n", calc_phi(n), calc_mu(n));
    }
    return 0;
}

 3.13 最大曼哈顿距离

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define N 100003
#define inf 1e100
double a[N][5];
int n;
 
int main() {
    while (scanf("%d", &n) == 1) {
        for (int i=0; i<n; i++)
            for (int j=0; j<5; j++) scanf("%lf", &a[i][j]);
        double ans = 0, mi, mx, t;
        for (int s=0; s<(1<<5); s++) {
            mi = inf, mx = -inf;
            for (int i=0; i<n; i++) {
                t = 0;
                for (int j=0; j<5; j++)
                    if ((1<<j) & s) t += a[i][j];
                    else t -= a[i][j];
                mi = min(mi, t);
                mx = max(mx, t);
            }
            ans = max(ans, mx-mi);
        }
        printf("%.2lf\n", ans);
    }
    return 0;
}

 

 

 

 

 

四.技巧

4.1 imos累积和法

//http://www.hankcs.com/program/algorithm/imos_method.html
//算法用于计算二维平面最大高度点，原理左上右下标1，左下右上标-1，累加求最大。
#include <iostream>
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
#define  W  6
#define  H  6
#define  N  4
// 左下角坐标
int B[N] = {3,4,3,5,};
int C[N] = {0,1,2,2,};
// 右上角坐标
int A[N] = {0,3,2,2,};
int D[N] = {3,2,3,5,};
// 地图上的分布结果
int tiles[H][W];

///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
    memset(tiles, 0, sizeof(tiles));
    // 影响力计算 (图 3)
    for (int i = 0; i < N; i++)
    {
        tiles[C[i]][A[i]]++;
        tiles[C[i]][B[i]]--;
        tiles[D[i]][A[i]]--;
        tiles[D[i]][B[i]]++;
    }
    // 横向累积和 (图 4, 5)
    for (int y = 0; y < H; y++)
    {
        for (int x = 1; x < W; x++)
        {
            tiles[y][x] += tiles[y][x - 1];
        }
    }
    // 纵向累积和 (图 6, 7)
    for (int y = 1; y < H; y++)
    {
        for (int x = 0; x < W; x++)
        {
            tiles[y][x] += tiles[y - 1][x];
        }
    }

    cout << *max_element(tiles[0], tiles[0] + H * W) << endl;
    system("pause");
    return 0;
}
///////////////////////////End Sub//////////////////////////////////

4.2 坐标离散化

//http://www.hankcs.com/program/algorithm/aoj-0531-paint-color.html
#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
#include <cstring>
#define MAX_N 1000 + 16
 
using namespace std;
 
int N, H, W;
int X1[MAX_N], X2[MAX_N], Y1[MAX_N], Y2[MAX_N];
int fld[2 * MAX_N][2 * MAX_N], // 填充遍历用，代表坐标(i, j)处是否空白（压缩后）
dx[4] = { 1, -1, 0, 0 }, dy[4] = { 0, 0, 1, -1 };

// 压缩坐标，将坐标的值变成“这是第几种值”，返回一共有几种坐标
int compress(int *x1, int *x2, int w)
{
    vector<int>xs;
 
    for (int i = 0; i < N; ++i)
    {
        int tx1 = x1[i], tx2 = x2[i];
        if (1 <= tx1 && tx1 < w) xs.push_back(tx1);
        if (1 <= tx2 && tx2 < w) xs.push_back(tx2);
    }
    xs.push_back(0);
    xs.push_back(w);
    sort(xs.begin(), xs.end());
    xs.erase(unique(xs.begin(), xs.end()), xs.end());
    for (int i = 0; i < N; ++i)
    {
        x1[i] = find(xs.begin(), xs.end(), x1[i]) - xs.begin();
        x2[i] = find(xs.begin(), xs.end(), x2[i]) - xs.begin();
    }
    return xs.size() - 1;
}
 
int bfs()
{
    int ans = 0;
    for (int i = 0; i < H; ++i)
    {
        for (int j = 0; j < W; ++j)
        {
            if (fld[i][j]) continue;
            ++ans;
            queue<pair<int, int> >que;
            que.push(make_pair(j, i));
            while (!que.empty())
            {
                int nx = que.front().first, ny = que.front().second;
                que.pop();
 
                for (int i = 0; i < 4; ++i)
                {
                    int tx = nx + dx[i], ty = ny + dy[i];
                    if (tx < 0 || W < tx || ty < 0 || H< ty || fld[ty][tx] > 0) continue;
                    que.push(make_pair(tx, ty));
                    fld[ty][tx] = 1;
                }
            }
        }
    }
    return ans;
}
 
///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
    while (cin >> W >> H, W | H)
    {
        cin >> N;
        for (int i = 0; i < N; ++i)
        {
            cin >> X1[i] >> Y1[i] >> X2[i] >> Y2[i];
        }
 
        memset(fld, 0, sizeof(fld));
 
        W = compress(X1, X2, W);
        H = compress(Y1, Y2, H);
 
        // imos-法
        for (int i = 0; i < N; i++)
        {
            fld[Y1[i]][X1[i]]++;
            fld[Y1[i]][X2[i]]--;
            fld[Y2[i]][X1[i]]--;
            fld[Y2[i]][X2[i]]++;
        }
        // 横向累积
        for (int i = 0; i < H; i++)
        {
            for (int j = 1; j < W; j++)
            {
                fld[i][j] += fld[i][j - 1];
            }
        }
        // 纵向累积
        for (int i = 1; i < H; i++)
        {
            for (int j = 0; j < W; j++)
            {
                fld[i][j] += fld[i - 1][j];
            }
        }// 累积完后，fld中非0部分表示有挡板
        cout << bfs() << endl;
    }
    return 0;
}
///////////////////////////End Sub//////////////////////////////////

4.3 博弈sg模板

//f[]：可以取走的石子个数  
//sg[]:0~n的SG函数值  
//hash[]:mex{}  
int f[N],sg[N],hash[N];       
void getSG(int n)  
{  
    int i,j;  
    memset(sg,0,sizeof(sg));  
    for(i=1;i<=n;i++)  
    {  
        memset(hash,0,sizeof(hash));  
        for(j=1;f[j]<=i;j++)  
            hash[sg[i-f[j]]]=1;  
        for(j=0;j<=n;j++)    //求mes{}中未出现的最小的非负整数  
        {  
            if(hash[j]==0)  
            {  
                sg[i]=j;  
                break;  
            }  
        }  
    }  
}  

//注意 S数组要按从小到大排序 SG函数要初始化为-1 对于每个集合只需初始化1遍  
//n是集合s的大小 S[i]是定义的特殊取法规则的数组  
int s[110],sg[10010],n;  
int SG_dfs(int x)  
{  
    int i;  
    if(sg[x]!=-1)  
        return sg[x];  
    bool vis[110];  
    memset(vis,0,sizeof(vis));  
    for(i=0;i<n;i++)  
    {  
        if(x>=s[i])  
        {  
            SG_dfs(x-s[i]);  
            vis[sg[x-s[i]]]=1;  
        }  
    }  
    int e;  
    for(i=0;;i++)  
        if(!vis[i])  
        {  
            e=i;  
            break;  
        }  
    return sg[x]=e;  
} 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <set>

using namespace std;

const int maxn = 10005;

int sg[maxn];

void SG()
{
    sg[0] = 0;
    for(int i = 2;i <= maxn; i++) {
        set<int>s;
        for(int j = 2;j <= 9; j++) {
            int temp = i/j;
            if(i%j) temp++;
            s.insert(sg[temp]);
        }
        int now = 0;
        while(s.count(now)) now++;
        sg[i] = now;
    }
}
/**
    打表发现：先手1~9，19~162，325~2916必胜
    满足前一个区间l,r->r*2+1,(r*2)*9
*/


int main()
{
    //SG();
    //freopen("in.txt","r",stdin);
    int n;
    while(scanf("%d",&n) != EOF) {
        int l = 1,r = 9;
        int flag = 1;
        while(1) {
            if(l <= n && n <= r) {
                flag = true;
                break;
            }
            else if(n < l) {
                flag = false;
                break;
            }
            l = r*2+1;
            r = r*2*9;
        }
        if(flag)
            printf("Stan wins.\n");
        else
            printf("Ollie wins.\n");
    }

    return 0;
}

 4.4 RMQ（区间极值查询）

void ST(int n) {
    for (int i = 1; i <= n; i++)
        dp[i][0] = A[i];
    for (int j = 1; (1 << j) <= n; j++) {
        for (int i = 1; i + (1 << j) - 1 <= n; i++) {
            dp[i][j] = max(dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1]);
        }
    }
}
int RMQ(int l, int r) {
    int k = 0;
    while ((1 << (k + 1)) <= r - l + 1) k++;
    return max(dp[l][k], dp[r - (1 << k) + 1][k]);
}

 4.5 二维RMQ

#include<iostream>
#include<cstdio>
#include<string.h>
#include<string>
#include<stack>
#include<set>
#include<algorithm>
#include<cmath>
#include<vector>
#include<map>


#define ll __int64
#define lll unsigned long long
#define MAX 1000009
#define eps 1e-8

using namespace std;
/*
二维RMQ模板题
同一维一样 用dp[row][col][i][j]表示(row,col)到(row+2^i,col+2^j)矩形内的最小值
查询
*/

int mapp[309][309];
int dp[309][309][9][9];
int flag;

void RMQ_init2d(int m,int n)
{
    for(int i=1; i<=m; i++)
    {
        for(int j = 1; j<=n; j++)
        {
            dp[i][j][0][0] = mapp[i][j];
        }
    }
    int t = log((double)n) / log(2.0);

    for(int i = 0; i<=t; i++)
    {
        for(int j = 0; j<=t; j++)
        {
            if(i==0&&j==0)
                continue;
            for(int row = 1; row+(1<<i)-1<= m; row++)
            {
                for(int col = 1; col+(1<<j)-1<= n; col++)
                {
                    if(i)
                        dp[row][col][i][j]  = max(dp[row][col][i-1][j],dp[row+(1<<(i-1))][col][i-1][j]);
                    else
                        dp[row][col][i][j]  = max(dp[row][col][i][j-1],dp[row][col+(1<<(j-1))][i][j-1]);
                }
            }
        }
    }
}
int RMQ_2d(int x1,int y1,int x2,int y2)
{
    int k1 = log(double(x2 - x1 + 1)) / log(2.0);
    int k2 = log(double(y2 - y1 + 1)) / log(2.0);
    int m1 = dp[x1][y1][k1][k2];
    int m2 = dp[x2 - (1<<k1) + 1][y1][k1][k2];
    int m3 = dp[x1][y2 - (1<<k2) + 1][k1][k2];
    int m4 = dp[x2 - (1<<k1) + 1][y2 - (1<<k2) + 1 ][k1][k2];
    int _max = max(max(m1,m2),max(m3,m4));
    if(mapp[x1][y1]==_max||mapp[x1][y2]==_max||mapp[x2][y1]==_max||mapp[x2][y2]==_max)
        flag = 1;
    return _max;
}

int main()
{
    int n,m,t;
    int x1,x2,y1,y2;
    while(~scanf("%d%d",&m,&n))
    {
        for(int i = 1; i<=m; i++)
        {
            for(int j = 1; j<=n; j++)
            {
                scanf("%d",&mapp[i][j]);
            }
        } 
        RMQ_init2d(m,n);
        scanf("%d",&t);
        while(t--)
        {
            scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
           
            flag = 0;
            int _max = RMQ_2d(x1,y1,x2,y2);
            if(flag == 1)
                printf("%d yes\n",_max);
            else
                printf("%d no\n",_max);
        }
    }
    return 0;
}

 

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;

int val[255][255];
int mm[255];
int dpmin[255][255][8][8];//最小值
int dpmax[255][255][8][8];//最大值

void initRMQ(int n,int m)
{
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
            dpmin[i][j][0][0] = dpmax[i][j][0][0] = val[i][j];
    for(int ii = 0; ii <= mm[n]; ii++)
        for(int jj = 0; jj <= mm[m]; jj++)
            if(ii+jj)
                for(int i = 1; i + (1<<ii) - 1 <= n; i++)
                    for(int j = 1; j + (1<<jj) - 1 <= m; j++)
                    {
                        if(ii)
                        {
                            dpmin[i][j][ii][jj] = min(dpmin[i][j][ii-1][jj],dpmin[i+(1<<(ii-1))][j][ii-1][jj]);
                            dpmax[i][j][ii][jj] = max(dpmax[i][j][ii-1][jj],dpmax[i+(1<<(ii-1))][j][ii-1][jj]);
                        }
                        else
                        {
                            dpmin[i][j][ii][jj] = min(dpmin[i][j][ii][jj-1],dpmin[i][j+(1<<(jj-1))][ii][jj-1]);
                            dpmax[i][j][ii][jj] = max(dpmax[i][j][ii][jj-1],dpmax[i][j+(1<<(jj-1))][ii][jj-1]);
                        }
                    }
}
//查询矩形的最大值
int rmq1(int x1,int y1,int x2,int y2)
{
    int k1 = mm[x2-x1+1];
    int k2 = mm[y2-y1+1];
    x2 = x2 - (1<<k1) + 1;
    y2 = y2 - (1<<k2) + 1;
    return max(max(dpmax[x1][y1][k1][k2],dpmax[x1][y2][k1][k2]),max(dpmax[x2][y1][k1][k2],dpmax[x2][y2][k1][k2]));
}
//查询矩形的最小值
int rmq2(int x1,int y1,int x2,int y2)
{
    int k1 = mm[x2-x1+1];
    int k2 = mm[y2-y1+1];
    x2 = x2 - (1<<k1) + 1;
    y2 = y2 - (1<<k2) + 1;
    return min(min(dpmin[x1][y1][k1][k2],dpmin[x1][y2][k1][k2]),min(dpmin[x2][y1][k1][k2],dpmin[x2][y2][k1][k2]));
}


int main()
{
    mm[0] = -1;
    for(int i = 1;i <= 500;i++)
        mm[i] = ((i&(i-1))==0)?mm[i-1]+1:mm[i-1];
    int N,B,K;
    while(scanf("%d%d%d",&N,&B,&K)==3)
    {
        for(int i = 1;i <= N;i++)
            for(int j = 1;j <= N;j++)
                scanf("%d",&val[i][j]);
        initRMQ(N,N);
        int x,y;
        while(K--)
        {
            scanf("%d%d",&x,&y);
            printf("%d\n",rmq1(x,y,x+B-1,y+B-1)-rmq2(x,y,x+B-1,y+B-1));
        }
    }
    return 0;
}

 

 

4.6 莫队算法

#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<math.h>
#include<cstring>
#define go(i,a,b) for(int i=a;i<=b;i++)
#define mem(a,b) memset(a,b,sizeof(a))
#define ll long long
using namespace std;const int N=50003;
struct Mo{int l,r,ID;ll A,B;}q[N];ll S(ll x){return x*x;}
ll GCD(ll a,ll b){while(b^=a^=b^=a%=b);return a;}
int n,m,col[N],unit,Be[N];ll sum[N],ans;
bool cmp(Mo a,Mo b){return Be[a.l]==Be[b.l]?a.r<b.r:a.l<b.l;}
bool CMP(Mo a,Mo b){return a.ID<b.ID;};
void revise(int x,int add){ans-=S(sum[col[x]]),sum[col[x]]+=add,ans+=S(sum[col[x]]);}
int main()
{
    scanf("%d%d",&n,&m);unit=sqrt(n);
    go(i,1,n)scanf("%d",&col[i]),Be[i]=i/unit+1;;
    go(i,1,m)scanf("%d%d",&q[i].l,&q[i].r),q[i].ID=i;

    sort(q+1,q+m+1,cmp);

    int l=1,r=0;
    go(i,1,m)
    {
        while(l<q[i].l)revise(l,-1),l++;
        while(l>q[i].l)revise(l-1,1),l--;
        while(r<q[i].r)revise(r+1,1),r++;
        while(r>q[i].r)revise(r,-1),r--;

        if(q[i].l==q[i].r){q[i].A=0;q[i].B=1;continue;}
        q[i].A=ans-(q[i].r-q[i].l+1);
        q[i].B=1LL*(q[i].r-q[i].l+1)*(q[i].r-q[i].l);
        ll gcd=GCD(q[i].A,q[i].B);q[i].A/=gcd;q[i].B/=gcd;
    }

    sort(q+1,q+m+1,CMP);
    go(i,1,m)printf("%lld/%lld\n",q[i].A,q[i].B);
    return 0;
}//Paul_Guderian

带修莫队

#include<stdio.h>
#include<algorithm>
#include<math.h>
#define go(i,a,b) for(int i=a;i<=b;i++)
using namespace std;const int N=10003;
struct Query{int l,r,Tim,ID;}q[N];
struct Change{int pos,New,Old;}c[N];
int n,m,s[N],color[N*100],t,Time,now[N],unit,Be[N],ans[N],Ans,l=1,r,T;
bool cmp(Query a,Query b)
{
    return Be[a.l]==Be[b.l]?(Be[a.r]==Be[b.r]?a.Tim<b.Tim:a.r<b.r):a.l<b.l;
}
void revise(int x,int d){color[x]+=d;if(d>0)Ans+=color[x]==1;if(d<0)Ans-=color[x]==0;}
void going(int x,int d){if(l<=x&&x<=r)revise(d,1),revise(s[x],-1);s[x]=d;}
int main(){
    scanf("%d%d",&n,&m);unit=pow(n,0.666666);
    go(i,1,n)scanf("%d",&s[i]),now[i]=s[i],Be[i]=i/unit+1;
    go(i,1,m){char sign;int x,y;scanf(" %c %d%d",&sign,&x,&y);
        if(sign=='Q')q[++t]=(Query){x,y,Time,t};
        if(sign=='R')c[++Time]=(Change){x,y,now[x]},now[x]=y;
    }
    sort(q+1,q+t+1,cmp);go(i,1,t)
    {
        while(T<q[i].Tim)going(c[T+1].pos,c[T+1].New),T++;
        while(T>q[i].Tim)going(c[T].pos,c[T].Old),T--;
        
        while(l<q[i].l)revise(s[l],-1),l++;
        while(l>q[i].l)revise(s[l-1],1),l--;
        while(r<q[i].r)revise(s[r+1],1),r++;
        while(r>q[i].r)revise(s[r],-1),r--;
        
        ans[q[i].ID]=Ans;
    }
    go(i,1,t)printf("%d\n",ans[i]);return 0;
}//Paul_Guderian

树上莫队

#include<stdio.h>
#include<algorithm>
#include<math.h>
#define go(i,a,b) for(int i=a;i<=b;i++)
#define ro(i,a,b) for(int i=a;i>=b;i--)
#define fo(i,a,x) for(int i=a[x],v=e[i].v;i;i=e[i].next,v=e[i].v)
using namespace std;const int N=50009;
struct E{int v,next;}e[N*3];
int k=1,head[N],unit,Be[N],m,st[N],top,fa[N][18],deep[N];
int n,Q,a[N],t[N],op,x,y,p,tim,u=1,v=1,T,ans[N],vis[N];
void ADD(int u,int v){e[k]=(E){v,head[u]};head[u]=k++;}
void dfs(int u){
    
    go(i,1,19)if((1<<i)>deep[u])break;
    else fa[u][i]=fa[fa[u][i-1]][i-1];
        
    int bottom=top;
    fo(i,head,u)if(v!=fa[u][0])
    {
        fa[v][0]=u;deep[v]=deep[u]+1;dfs(v);
        if(top-bottom>=unit){m++;while(top!=bottom)Be[st[top--]]=m;}
    }
    st[++top]=u;
}
int LCA(int x,int y)
{
    if(deep[x]<deep[y])swap(x,y);int Dis=deep[x]-deep[y];
    go(i,0,16)if((1<<i)&Dis)x=fa[x][i];
    if(x==y)return x;
    ro(i,16,0)if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
    return x==y?x:fa[x][0];
}
struct Change{int u,New,Old;}cq[N];
struct Query{int u,v,tim,id;bool operator <(const Query &a) const{
    return Be[u]==Be[a.u]?(Be[v]==Be[a.v]?tim<a.tim:Be[v]<Be[a.v]):Be[u]<Be[a.u];
}}q[N];
struct Datalock{
    struct _blo{int l,r;}b[350];
    int n,Be[N],m,unit,num[N],sum[350];
    void init()
    {
        unit=sqrt(n);m=(n-1)/unit+1;
        go(i,1,n)Be[i]=(i-1)/unit+1;
        go(i,1,m)b[i].l=(i-1)*unit+1,b[i].r=i*unit;
        b[m].r=n;
    }
    void Add(int v){if(v<=n)sum[Be[v]]+=(++num[v])==1;}
    void Del(int v){if(v<=n)sum[Be[v]]-=(--num[v])==0;}
    int mex()
    {
        go(i,1,m)if(sum[i]!=b[i].r-b[i].l+1)
        go(j,b[i].l,b[i].r)if(!num[j])return j;
        return -1;
    }
}Data;
void revise(int u,int d){if(vis[u])Data.Del(a[u]),Data.Add(d);a[u]=d;}
void Run(int u){if(vis[u])Data.Del(a[u]),vis[u]=0;else Data.Add(a[u]),vis[u]=1;}
void move(int x,int y)
{ 
    if(deep[x]<deep[y])swap(x,y);
    while(deep[x]>deep[y])Run(x),x=fa[x][0];
    while(x!=y)Run(x),Run(y),x=fa[x][0],y=fa[y][0];
}
void Mo()
{
    go(i,1,p)
    {
        while(T<q[i].tim)T++,revise(cq[T].u,cq[T].New);
        while(T>q[i].tim)revise(cq[T].u,cq[T].Old),T--;
        
        if(u!=q[i].u)move(u,q[i].u),u=q[i].u;
        if(v!=q[i].v)move(v,q[i].v),v=q[i].v;
        int anc=LCA(u,v);Run(anc);ans[q[i].id]=Data.mex()-1;Run(anc);
    }
}
int main(){scanf("%d%d",&n,&Q);unit=pow(n,0.45);
    go(i,1,n)scanf("%d",&a[i]),t[i]=++a[i];
    go(i,2,n){int uu,vv;scanf("%d%d",&uu,&vv);ADD(uu,vv);ADD(vv,uu);}
    dfs(1);while(top)Be[st[top--]]=m;
    go(i,1,Q)
    {
        scanf("%d%d%d",&op,&x,&y);
        if( op)p++,q[p]=(Query){x,y,tim,p};
        if(!op)tim++,cq[tim]=(Change){x,y+1,t[x]},t[x]=y+1;
    } 
    Data.n=n+1;Data.init();sort(q+1,q+1+p);Mo();
    go(i,1,p)printf("%d\n",ans[i]);
}//Paul_Guderian

 C（n，k）

/*20180802
题意：求sum（C（n，k）） 0<=i<=k;
数据范围1e5.
莫队算法：推出递推公式。
按块排序使得顺序解题效率最优
*/
#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<math.h>
#include<cstring>
#define go(i,a,b) for(int i=a;i<=b;i++)
#define mem(a,b) memset(a,b,sizeof(a))
#define ll long long
using namespace std;
const int N=100100;
const int MOD=1000000007;
int fac[N], inv[N], res[N], in_chunk[N];
int cnt, mx=100010, chunk,T;
//每次询问
struct Mo{int n,k,ID;ll ans;}q[N];

int powi(int a, int b)
{
    int c = 1;
    for (; b; b >>= 1, a = 1ll * a * a % MOD)
        if (b & 1) c = 1ll * c * a % MOD;
    return c;
}
int C(int a, int b)
{
    return 1ll * fac[a] * inv[b] % MOD * inv[a - b] % MOD;
}

int n,unit,Be[N];ll ans;
//按块双关键词排序，使得k在变化过程中一定比n小
bool cmp(Mo a,Mo b){return Be[a.k]==Be[b.k]?a.n<b.n:a.k<b.k;}
bool CMP(Mo a,Mo b){return a.ID<b.ID;}

int main()
{

    fac[0] = 1; for (int i = 1; i <= 100010; ++ i) fac[i] = 1ll * fac[i - 1] * i % MOD;
    inv[mx] = powi(fac[mx], MOD - 2); for (int i = mx - 1; ~i; -- i) inv[i] = 1ll * inv[i + 1] * (i + 1) % MOD;


    scanf("%d",&T);unit=sqrt(100000);
    for(int i=0;i<=100000;i++)Be[i]=i/unit+1;
    go(i,1,T)scanf("%d%d",&q[i].n,&q[i].k),q[i].ID=i;

    sort(q+1,q+T+1,cmp);
    int in=0,ik=0;
    ans=1;
    go(i,1,T)
    {
        while(in<q[i].n){
            if(ik==0){
                in=q[i].n;
                ans=1;
            }
            else {
                ans=(2*ans-C(in,ik)+MOD)%MOD;
                in++;
            }
        }
        while(in>q[i].n){
            if(ik==0){
                in=q[i].n;
                ans=1;
            }
            else {
                ans=(ans+C(in-1,ik))%MOD*inv[2]%MOD;
                in--;
            }
        }
        while(ik<q[i].k){
            ans=(ans+C(in,ik+1))%MOD;
            ik++;
        }
        while(ik>q[i].k){
            ans=(ans-C(in,ik)+MOD)%MOD;
            ik--;
        }
        q[i].ans=ans;
    }
    sort(q+1,q+T+1,CMP);
    go(i,1,T)printf("%lld\n",q[i].ans);
    return 0;
}//Paul_Guderian

 区间覆盖问题

#include<iostream>
#include<stdio.h>
#include<algorithm>
using namespace std;


int main()
{
    int T, n, s[250001], t[250001];
    int m;
    double sum=0;
        cin >> n>>m;
        for (int i = 1; i <= n; i++){
                scanf("%d%d", &s[i], &t[i]);
                sum+=t[i]-s[i]+1;
        }
        sort(s + 1, s + n + 1);
        sort(t + 1, t + n + 1);
        int ans = 0;
        for (int i = 1, j = 1; i <= n;)
        {
            if (s[i] <= t[j])
            {
                if (ans < i - j)ans = i - j;
                i++;
            }
            else j++;
        }
        cout << ans + 1 << endl;
        printf("%.20lf\n",sum/m);

    return 0;
}

 

 

五.图论

5.1 并查集

//https://blog.csdn.net/u013486414/article/details/38682057
const int MAXSIZE = 500;

int uset[MAXSIZE];

int rank[MAXSIZE];

 

void makeSet(int size) {

    for(int i = 0;i < size;i++)  uset[i] = i;

    for(int i = 0;i < size;i++)  rank[i] = 0;

}

int find(int x) {

    if (x != uset[x]) uset[x] = find(uset[x]);

    return uset[x];

}

void unionSet(int x, int y) {

    if ((x = find(x)) == (y = find(y))) return;

    if (rank[x] > rank[y]) uset[y] = x;

    else {

        uset[x] = y;

        if (rank[x] == rank[y]) rank[y]++;

    }

}

5.2 求图中任意两点的最短距离的 弗洛伊德算法 

//https://blog.csdn.net/qq_16657927/article/details/79942140
/* 
    |Floyd算法| 
    |任意点对最短路算法| 
    |求图中任意两点的最短距离的算法| 
*/  
  
for (int k = 0; k < n; k++) {    
    for (int i = 0; i < n; i++) {    
        for (int j = 0; j < n; j++) {    
            dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);    
        }    
    }  
}  

5.3 最小生成树·Kruskal

//https://blog.csdn.net/qq_16657927/article/details/79942140
/* 
    |Kruskal算法| 
    |适用于 稀疏图 求最小生成树| 
    |16/11/05ztx thanks to wangqiqi| 
*/  
  
/* 
    第一步：点、边、加入vector，把所有边按从小到大排序 
    第二步：并查集部分 + 下面的code 
*/  
  
void Kruskal() {      
    ans = 0;      
    for (int i = 0; i<len; i++) {      
        if (Find(edge[i].a) != Find(edge[i].b)) {      
            Union(edge[i].a, edge[i].b);      
            ans += edge[i].len;      
        }      
    }      
}     

5.4 最小生成树· prim算法

//https://blog.csdn.net/qq_16657927/article/details/79942140
/*
    |Prim算法|
    |适用于 稠密图 求最小生成树|
    |堆优化版，时间复杂度：O(elgn)|
    |16/11/05ztx, thanks to chaixiaojun|
*/

struct node {  
    int v, len;  
    node(int v = 0, int len = 0) :v(v), len(len) {}  
    bool operator < (const node &a)const {  // 加入队列的元素自动按距离从小到大排序  
        return len> a.len;  
    }  
};

vector<node> G[maxn];
int vis[maxn];
int dis[maxn];

void init() {  
    for (int i = 0; i<maxn; i++) {  
        G[i].clear();  
        dis[i] = INF;  
        vis[i] = false;  
    }  
}  
int Prim(int s) {  
    priority_queue<node>Q; // 定义优先队列  
    int ans = 0;  
    Q.push(node(s,0));  // 起点加入队列  
    while (!Q.empty()) {   
        node now = Q.top(); Q.pop();  // 取出距离最小的点  
        int v = now.v;  
        if (vis[v]) continue;  // 同一个节点，可能会推入2次或2次以上队列，这样第一个被标记后，剩下的需要直接跳过。  
        vis[v] = true;  // 标记一下  
        ans += now.len;  
        for (int i = 0; i<G[v].size(); i++) {  // 开始更新  
            int v2 = G[v][i].v;  
            int len = G[v][i].len;  
            if (!vis[v2] && dis[v2] > len) {   
                dis[v2] = len;  
                Q.push(node(v2, dis[v2]));  // 更新的点加入队列并排序  
            }  
        }  
    }  
    return ans; 
}  

//https://blog.csdn.net/qq_16657927/article/details/79942140
#include<iostream>
#include<string>
#include<vector>
using  namespace std;

//首先是使用邻接矩阵完成Prim算法
struct Graph {
    int vexnum;  //顶点个数
    int edge;   //边的条数
    int ** arc; //邻接矩阵
    string *information; //记录每个顶点名称
};

//创建图
void createGraph(Graph & g) {
    cout << "请输入顶点数：输入边的条数" << endl;
    cin >> g.vexnum;
    cin >> g.edge;  //输入边的条数

    g.information = new string[g.vexnum];
    g.arc = new int*[g.vexnum];
    int i = 0;

    //开辟空间的同时，进行名称的初始化
    for (i = 0; i < g.vexnum; i++) {
        g.arc[i] = new int[g.vexnum];
        g.information[i]="v"+ std::to_string(i+1);//对每个顶点进行命名
        for (int k = 0; k < g.vexnum; k++) {
            g.arc[i][k] = INT_MAX;          //初始化我们的邻接矩阵
        }
    }

    cout << "请输入每条边之间的顶点编号(顶点编号从1开始),以及该边的权重：" << endl;
    for (i = 0; i < g.edge; i++) {
        int start;
        int end;
        cin >> start;   //输入每条边的起点
        cin >> end;     //输入每条边的终点
        int weight;
        cin >> weight;
        g.arc[start-1][end-1]=weight;//无向图的边是相反的
        g.arc[end-1][start-1] = weight;
    }
}

//打印图
void print(Graph g) {
    int i;
    for (i = 0; i < g.vexnum; i++) {
        //cout << g.information[i] << " ";
        for (int j = 0; j < g.vexnum; j++) {
            if (g.arc[i][j] == INT_MAX)
                cout << "∞" << " ";
            else
            cout << g.arc[i][j] << " ";
        }
        cout << endl;
    }
}

//作为记录边的信息，这些边都是达到end的所有边中，权重最小的那个
struct Assis_array {
    int start; //边的终点
    int end;  //边的起点
    int weight;  //边的权重
};
//进行prim算法实现，使用的邻接矩阵的方法实现。
void Prim(Graph g,int begin) {

    //close_edge这个数组记录到达某个顶点的各个边中的权重最大的那个边
    Assis_array *close_edge=new Assis_array[g.vexnum];

    int j;

    //进行close_edge的初始化，更加开始起点进行初始化
    for (j = 0; j < g.vexnum; j++) {
        if (j != begin - 1) {
            close_edge[j].start = begin-1;
            close_edge[j].end = j;
            close_edge[j].weight = g.arc[begin - 1][j];
        }
    }
    //把起点的close_edge中的值设置为-1，代表已经加入到集合U了
    close_edge[begin - 1].weight = -1;
    //访问剩下的顶点，并加入依次加入到集合U
    for (j = 1; j < g.vexnum; j++) {

        int min = INT_MAX;
        int k;
        int index;
        //寻找数组close_edge中权重最小的那个边
        for (k = 0; k < g.vexnum; k++) {
            if (close_edge[k].weight != -1) {  
                if (close_edge[k].weight < min) {
                    min = close_edge[k].weight;
                    index = k;
                }
            }
        }
        //将权重最小的那条边的终点也加入到集合U
        close_edge[index].weight = -1;
        //输出对应的边的信息
        cout << g.information[close_edge[index].start] 
            << "-----" 
            << g.information[close_edge[index].end]
            << "="
            <<g.arc[close_edge[index].start][close_edge[index].end]
            <<endl;

        //更新我们的close_edge数组。
        for (k = 0; k < g.vexnum; k++) {
            if (g.arc[close_edge[index].end][k] <close_edge[k].weight) {
                close_edge[k].weight = g.arc[close_edge[index].end][k];
                close_edge[k].start = close_edge[index].end;
                close_edge[k].end = k;
            }
        }
    }
}



int main()
{
    Graph g;
    createGraph(g);//基本都是无向网图，所以我们只实现了无向网图
    print(g);
    Prim(g, 1);
    system("pause");
    return 0;
}

5.5 染色法

/* 
    |交叉染色法判断二分图| 
    |16/11/05ztx| 
*/  
  
int bipartite(int s) {    
    int u, v;    
    queue<int>Q;    
    color[s] = 1;    
    Q.push(s);    
    while (!Q.empty()) {    
        u = Q.front();    
        Q.pop();    
        for (int i = 0; i < G[u].size(); i++) {    
            v = G[u][i];    
            if (color[v] == 0) {    
                color[v] = -color[u];    
                Q.push(v);    
            }    
            else if (color[v] == color[u])    
                return 0;    
        }    
    }    
    return 1;    
}    

5.6 匈牙利算法

//https://blog.csdn.net/qq_16657927/article/details/79942140
/* 
    |求解最大匹配问题| 
    |递归实现| 
    |16/11/05ztx| 
*/  
  
vector<int>G[maxn];    
bool inpath[maxn];  //  标记    
int match[maxn];    //  记录匹配对象    
void init()    
{    
    memset(match, -1, sizeof(match));    
    for (int i = 0; i < maxn; ++i) {    
        G[i].clear();    
    }    
}    
bool findpath(int k) {    
    for (int i = 0; i < G[k].size(); ++i) {    
        int v = G[k][i];    
        if (!inpath[v]) {    
            inpath[v] = true;    
            if (match[v] == -1 || findpath(match[v])) { // 递归    
                match[v] = k; // 即匹配对象是“k妹子”的    
                return true;    
            }    
        }    
    }    
    return false;    
}    
  
void hungary() {    
    int cnt = 0;    
    for (int i = 1; i <= m; i++) {  // m为需要匹配的“妹子”数    
        memset(inpath, false, sizeof(inpath)); // 每次都要初始化    
        if (findpath(i)) cnt++;    
    }    
    cout << cnt << endl;    
}    

/* 
    |求解最大匹配问题| 
    |dfs实现| 
    |16/11/05ztx| 
*/  
  
int v1, v2;    
bool Map[501][501];    
bool visit[501];    
int link[501];    
int result;    
  
bool dfs(int x)  {    
    for (int y = 1; y <= v2; ++y)  {    
        if (Map[x][y] && !visit[y])  {    
            visit[y] = true;    
            if (link[y] == 0 || dfs(link[y]))  {    
                link[y] = x;    
                return true;    
            } } }    
    return false;    
}    
  
  
void Search()  {    
    for (int x = 1; x <= v1; x++)  {    
        memset(visit,false,sizeof(visit));    
        if (dfs(x))    
            result++;    
    }  
}  

 5.7 Dijstra算法

//https://blog.csdn.net/mengxiang000000/article/details/50421243
#include<stdio.h>
#include<string.h>
#include<iostream>
using namespace std;
#define N 0x1f1f1f1f
int w[151][151];
int d[155];
int ans,vis[151];
int n,m;
void Dij()
{
    int i,j,k,v,tmp;
    memset(vis,0,sizeof(vis));
    for(i=1;i<=n;i++)
        d[i]=w[1][i];
    d[1]=0;
    vis[1]=1;
    for(i=1;i<=n;i++)
    {
        tmp=N;
        for(j=1;j<=n;j++)
        {
            if(tmp>d[j]&&!vis[j])
            {
                tmp=d[j];
                v=j;
            }
        }
        vis[v]=1;
        for(k=1;k<=n;k++)
        {
            if(!vis[k])
            d[k]=min(d[k],d[v]+w[v][k]);
        }
    }
}
int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        if(n==0&&m==0)break;
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                w[i][j]=0x1f1f1f1f;
            }
        }
        for(int i=0;i<m;i++)
        {
            int a,b,dis;
            scanf("%d%d%d",&a,&b,&dis);
            if(w[a][b]>dis)
            w[a][b]=w[b][a]=dis;
        }
        Dij();
        printf("%d\n",d[n]);
    }
}

 5.8 Bellman-ford算法

struct edge{int from,to,cost;};

edge es[MAX_E];

int d[MAX_V];
int V,E;

void shortest(int k){
    memset(d,0x3f,sizeof(d));
    d[k]=0;
    while(true){
        bool update=false;
        for(int i=0;i<E;i++){
            edge e=es[i];
            if(d[e.from]!=INF&&d[e.from]+e.cost<d[e.to]){
                d[e.to]=d[e.from]+e.cost;
                update=true;
            }
        }
        if(!update)break;
    }
}

 

5.11 拓扑排序

#include <iostream>
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <sstream>
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <cmath>
#define nmax 200
#define MEM(x) memset(x,0,sizeof(x))
using namespace std;
vector<int> v[nmax];
int indegree[nmax];
int n;
bool suc = true;
queue<int> ans;
void topsort()
{
    queue<int> q;
    while(1){
        for(int i = 1; i<=n ;++i){
            if(indegree[i] == 0){
                q.push(i);
                ans.push(i);
                indegree[i] = -1;
            }
        }
        if(q.empty()) break;
        while(!q.empty()){
            int t = q.front(); q.pop();
            for(int j = 0;j<v[t].size();++j){
                int tt = v[t][j];
                if(indegree[tt] == -1){
                    suc = false;
                    break;
                }else indegree[tt]--;
            }
            v[t].clear();
            if(!suc) break;
        }
        if(!suc) break;
    }
    if(ans.size() <n){
        suc =false;
        return;
    }
}
void output()
{
    bool isfirst = true;
    while(!ans.empty()){
        int t = ans.front(); ans.pop();
        if(isfirst){
            printf("%d",t);
            isfirst = false;
        }else
            printf(" %d",t);
    }
    printf("\n");
}
int main()
{
    //freopen("in.txt","r",stdin);
    int m;
    while(scanf("%d%d",&n,&m) ==2 && (n||m)){
        MEM(indegree);
        suc = true;
        int a,b;
        for(int i = 0; i<m; ++i){
            scanf("%d%d",&a,&b);
            indegree[b]++;
            v[a].push_back(b);
        }
        topsort();
        if(suc) output();
        else printf("failed\n");
    }
    return 0;
}

 5.12 数字游戏dfs记录路径

#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

bool flag;
LL a, b;
int tp;
LL link[1014];

void dfs(LL x);

int main(){
    while(~scanf("%lld %lld", &a, &b)){
        tp = 0, flag = false;
        link[tp++] = a;
        dfs(a);
        if(flag) {
            printf("YES\n");
            for(int i = 0; i < tp; i++)
                printf("%lld%c", link[i], i == tp-1? '\n': ' ');
        }
        else {
            printf("NO\n");
        }
    }
    return 0;
}
void dfs(LL x){
    if(flag || x > b) return;

    link[tp++] = x<<1;
    if(link[tp-1] == b){
        flag = true;
        return;
    }
    dfs(link[tp-1]);
    if(flag) return;
    else tp--;

    link[tp++] = x*(LL)10 + (LL)1;
    if(link[tp-1] == b){
        flag = true;
        return;
    }
    dfs(link[tp-1]);
    if(flag) return;
    else tp--;

    return;
}

 5.13 最长路径

// A C++ program to find single source longest distances in a DAG
#include <iostream>
#include <list>
#include <stack>
#include <limits.h>
#define NINF INT_MIN
using namespace std;

//图通过邻接表来描述。邻接表中的每个顶点包含所连接的顶点的数据，以及边的权值。
class AdjListNode
{
    int v;
    int weight;
public:
    AdjListNode(int _v, int _w)  { v = _v;  weight = _w;}
    int getV()       {  return v;  }
    int getWeight()  {  return weight; }
};

// Class to represent a graph using adjacency list representation
class Graph
{
    int V;    // No. of vertices’

    // Pointer to an array containing adjacency lists
    list<AdjListNode> *adj;

    // A function used by longestPath
    void topologicalSortUtil(int v, bool visited[], stack<int> &Stack);
public:
    Graph(int V);   // Constructor

    // function to add an edge to graph
    void addEdge(int u, int v, int weight);

    // Finds longest distances from given source vertex
    void longestPath(int s);
};

Graph::Graph(int V) // Constructor
{
    this->V = V;
    adj = new list<AdjListNode>[V];
}

void Graph::addEdge(int u, int v, int weight)
{
    AdjListNode node(v, weight);
    adj[u].push_back(node); // Add v to u’s list
}

// 通过递归求出拓扑序列. 详细描述，可参考下面的链接。
// http://www.geeksforgeeks.org/topological-sorting/
void Graph::topologicalSortUtil(int v, bool visited[], stack<int> &Stack)
{
    // 标记当前顶点为已访问
    visited[v] = true;

    // 对所有邻接点执行递归调用
    list<AdjListNode>::iterator i;
    for (i = adj[v].begin(); i != adj[v].end(); ++i)
    {
        AdjListNode node = *i;
        if (!visited[node.getV()])
            topologicalSortUtil(node.getV(), visited, Stack);
    }

    // 当某个点没有邻接点时，递归结束，将该点存入栈中。
    Stack.push(v);
}

// 根据传入的顶点，求出到到其它点的最长路径. longestPath使用了
// topologicalSortUtil() 方法获得顶点的拓扑序。
void Graph::longestPath(int s)
{
    stack<int> Stack;
    int dist[V];

    // 标记所有的顶点为未访问
    bool *visited = new bool[V];
    for (int i = 0; i < V; i++)
        visited[i] = false;

    // 对每个顶点调用topologicalSortUtil，最终求出图的拓扑序列存入到Stack中。
    for (int i = 0; i < V; i++)
        if (visited[i] == false)
            topologicalSortUtil(i, visited, Stack);

    //初始化到所有顶点的距离为负无穷
    //到源点的距离为0
    for (int i = 0; i < V; i++)
        dist[i] = NINF;
    dist[s] = 0;

    // 处理拓扑序列中的点
    while (Stack.empty() == false)
    {
        //取出拓扑序列中的第一个点
        int u = Stack.top();
        Stack.pop();

        // 更新到所有邻接点的距离
        list<AdjListNode>::iterator i;
        if (dist[u] != NINF)
        {
          for (i = adj[u].begin(); i != adj[u].end(); ++i)
             if (dist[i->getV()] < dist[u] + i->getWeight())
                dist[i->getV()] = dist[u] + i->getWeight();
        }
    }

    // 打印最长路径
    for (int i = 0; i < V; i++)
        (dist[i] == NINF)? cout << "INF ": cout << dist[i] << " ";
}
// Driver program to test above functions
int main()
{
    // Create a graph given in the above diagram.  Here vertex numbers are
    // 0, 1, 2, 3, 4, 5 with following mappings:
    // 0=r, 1=s, 2=t, 3=x, 4=y, 5=z
    Graph g(6);
    g.addEdge(0, 1, 5);
    g.addEdge(0, 2, 3);
    g.addEdge(1, 3, 6);
    g.addEdge(1, 2, 2);
    g.addEdge(2, 4, 4);
    g.addEdge(2, 5, 2);
    g.addEdge(2, 3, 7);
    g.addEdge(3, 5, 1);
    g.addEdge(3, 4, -1);
    g.addEdge(4, 5, -2);

    int s = 1;
    cout << "Following are longest distances from source vertex " << s <<" \n";
    g.longestPath(s);

    return 0;
}

 

六.数据结构

6.1 滑动区间最大值

#include<cstdio>
const int N=10000010;
int T,n,m,k,P,Q,R,MOD,i,a[N],q[N],h,t;long long A,B;
int main(){
  scanf("%d",&T);
  while(T--){
    scanf("%d%d%d%d%d%d%d",&n,&m,&k,&P,&Q,&R,&MOD);
    for(i=1;i<=k;i++)scanf("%d",&a[i]);
    for(i=k+1;i<=n;i++)a[i]=(1LL*P*a[i-1]+1LL*Q*i+R)%MOD;
    for(h=1,t=A=B=0,i=n;i;i--){
      while(h<=t&&a[q[t]]<=a[i])t--;
      q[++t]=i;
      if(i+m-1<=n){
        while(q[h]>=i+m)h++;
        A+=i^a[q[h]];
        B+=i^(t-h+1);
      }
    }
    printf("%lld %lld\n",A,B);
  }
}

6.2 树状数组

int lowbit(int i)
{
    return i & -i;//求数组下标数的二进制的非0最低位所表示的值
}
void update(int i,int val)//更新单节点的值
{
    while(i<=n){
        a[i]+=val;
        i+=lowbit(i);//由叶子节点向上更新a数组
    }
}
int sum(int i)//求和节点的值
{
    int ret=0;
    while(i>0){
        ret+=a[i];//从右往左区间求和
        i-=lowbit(i);
    }
    return ret;
}

    #include <iostream>
    #include <cstdio>
    #include <algorithm>
    #include <cmath>
    #include <cstring>
    using namespace std;
    int n,m,tree[2000010];
    int lowbit(int k)
    {
        return k & -k;
    }
    void add(int x,int k)
    {
        while(x<=n)
        {
            tree[x]+=k;
            x+=lowbit(x);
        }
    }
    int sum(int x)
    {
        int ans=0;
        while(x!=0)
        {
            ans+=tree[x];
            x-=lowbit(x);
        }
        return ans;
    }
    int main()
    {
        cin>>n>>m;
        for(int i=1;i<=n;i++)
        {
            int a;
            scanf("%d",&a);
            add(i,a);
        }
        for(int i=1;i<=m;i++)
        {
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            if(a==1)
                add(b,c);
            if(a==2)
                cout<<sum(c)-sum(b-1)<<endl;
        }
    }

    #include <iostream>
    #include <algorithm>
    #include <cstdio>
    #include <cstring>
    #include <cmath>
    #include <queue>
    using namespace std;
    int n,m;
    int input[500010];
    int tree[500100];
    int lowbit(int x)
    {
        return x & -x;
    }
    void add(int x,int k)
    {
        while(x<=n)
        {
            tree[x]+=k;
            x+=lowbit(x);
        }
    }
    int search(int x)
    {
        int ans=0;
        while(x!=0)
        {
            ans+=tree[x];
            x-=lowbit(x);
        }
        return ans;
    }
    int main()
    {
        cin>>n>>m;
        for(int i=1;i<=n;i++)
            cin>>input[i];
        for(int i=1;i<=m;i++)
        {
            int a;
            scanf("%d",&a);
            if(a==1)
            {
                int x,y,z;
                scanf("%d%d%d",&x,&y,&z);
                add(x,z);
                add(y+1,-z);
            }
            if(a==2)
            {
                int x;
                scanf("%d",&x);
                printf("%d\n",input[x]+search(x));
            }
        }
    }

 

 

6.3 划分树 区间第k大（小）

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define MAX_SIZE 100005
int sorted[MAX_SIZE];//已经排好序的数据
int toleft[25][MAX_SIZE];
int tree[25][MAX_SIZE];
void build_tree(int left, int right, int deep)
{
    int i;
    if (left == right) return ;
    int mid = (left + right) >> 1;
    int same = mid - left + 1; //位于左子树的数据
    for (i = left; i <= right; ++i) {//计算放于左子树中与中位数相等的数字个数
        if (tree[deep][i] < sorted[mid]) {
            --same;
        }
    }
    int ls = left;
    int rs = mid + 1;
    for (i = left; i <= right; ++i) {
        int flag = 0;
        if ((tree[deep][i] < sorted[mid]) || (tree[deep][i] == sorted[mid] && same > 0)) {
            flag = 1;
            tree[deep + 1][ls++] = tree[deep][i];
            if (tree[deep][i] == sorted[mid])
                same--;
        } else {
            tree[deep + 1][rs++] = tree[deep][i];
        }
        toleft[deep][i] = toleft[deep][i - 1]+flag;
    }
    build_tree(left, mid, deep + 1);
    build_tree(mid + 1, right, deep + 1);
}
int query(int left, int right, int k, int L, int R, int deep)
{
    if (left == right)
        return tree[deep][left];
    int mid = (L + R) >> 1;
    int x = toleft[deep][left - 1] - toleft[deep][L - 1];//位于left左边的放于左子树中的数字个数
    int y = toleft[deep][right] - toleft[deep][L - 1];//到right为止位于左子树的个数
    int ry = right - L - y;//到right右边为止位于右子树的数字个数
    int cnt = y - x;//[left,right]区间内放到左子树中的个数
    int rx = left - L - x;//left左边放在右子树中的数字个数
    if (cnt >= k) {
        //printf("sss %d %d %d\n", xx++, x, y);
        return query(L + x, L + y - 1, k, L, mid, deep + 1);
        // 因为x不在区间内 所以没关系 所以先除去，从L+x开始，然后确定范围
    }
    else {
        //printf("qqq %d %d %d\n", xx++, x, y);
        return query(mid + rx + 1, mid + 1 + ry, k - cnt, mid + 1, R, deep + 1);
        //同理 把不在区间内的 分到右子树的元素数目排除，确定范围
    }
}
int main()
{
    int m, n;
    int a, b, k;
    int i;
    while (scanf("%d%d", &m, &n) == 2) {
        for (i = 1; i <= m; ++i) {
            scanf("%d", &sorted[i]);
            tree[0][i] = sorted[i];
        }
        sort(sorted + 1, sorted + 1 + m);
        build_tree(1, m, 0);
        for (i = 0; i < n; ++i) {
            scanf("%d%d%d", &a, &b, &k);
            printf("%d\n", query(a, b, k, 1, m, 0));
        }
    }
    return 0;
}

 

 

 

七.字符串

7.1 Manacher 最长回文子串

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <map>
using namespace std;
 
const int N = 200010;
char s[N], str[N*2];
int p[N*2];
int manacher()
{
    int i;
    for(i = 1; s[i]; i++)
        str[i*2] = s[i], str[i*2+1] = '#';
    str[0] = '?', str[1] = '#', str[i*2] = '\0';
    int res = 0, k = 0, maxk = 0;
    for(int i = 2; str[i]; i++)
    {
        p[i] = i < maxk ? min(maxk - i, p[2*k-i]) : 1;
        while(str[i-p[i]] == str[i+p[i]]) p[i]++;
        if(p[i] + i > maxk)
            k = i, maxk = i + p[i];
        res = max(res, p[i]);
    }
    return res - 1;
}
 
int main()
{
    while(~ scanf(" %s", s + 1))
        printf("%d\n", manacher());
 
    return 0;
}

 7.2 最小/最大表示

int getMin(char *s)
{
    int i = 0, j = 1, l;
    int len = strlen(s);
    while(i < len && j < len)
    {
        for(l = 0; l < len; l++)
            if(s[(i + l) % len] != s[(j + l) % len]) break;
        if(l >= len) break;
        if(s[(i + l) % len] > s[(j + l) % len])
        {
            if(i + l + 1 > j) i = i + l + 1;
            else i = j + 1;
        }
        else if(j + l + 1 > i) j = j + l + 1;
        else j = i + 1;
    }
    return i < j ? i : j;
}
 
int getMax(char *s)
{
    int len = strlen(s);
    int i = 0, j = 1, k = 0;
    while(i < len && j < len && k < len)
    {
        int t = s[(i+k)%len]-s[(j+k)%len];
        if(!t) k++;
        else
        {
            if(t > 0)
            {
                if(j+k+1 > i) j = j+k+1;
                else j = i+1;
            }
            else if(i+k+1 > j) i = i+k+1;
            else i = j+1;
            k = 0;
        }
    }
    return i < j ? i : j;
}

 7.3 后缀数组

倍增法nlogn

#include <bits/stdc++.h>
using namespace std;

const int MAX_N=1000010;

int n,k;
int rank[MAX_N];
int tmp[MAX_N];
int sa[MAX_N];
//比较(rank[i],rank[i+k])和rank[j],rank[j+k]
bool compare_sa(int i,int j){
    if(rank[i]!=rank[j])return rank[i]<rank[j];
    else {
        int ri=i+k<=n?rank[i+k]:-1;
        int rj=j+k<=n?rank[j+k]:-1;
        return ri<rj;
    }
}

//计算字符串S的后缀数组
void construct_sa(string S,int *sa){
    n=S.length();

    //初始长度为1，rank直接截取字符编码
    for(int i=0;i<=n;i++){
        sa[i]=i;
        rank[i]=i<n?S[i]:-1;
    }

    //利用对长度为k的排序对长度为2k的排序
    for(k=1;k<=n;k*=2){
        sort(sa,sa+n+1,compare_sa);

        //先在tmp中临时存储新计算的rank，再转存回rank中
        tmp[sa[0]]=0;
        for(int i=1;i<=n;i++){
            tmp[sa[i]]=tmp[sa[i-1]] + (compare_sa(sa[i-1],sa[i]) ? 1 : 0) ;
        }
        for(int i=0;i<=n;i++){
            rank[i]=tmp[i];
        }
    }
}

int main(){
    string x;
    cin >> x;
    construct_sa(x,sa);
    for(int i=1;i<=x.size();i++){
        printf("%d ",sa[i]+1);
    }
    printf("\n");
}

加桶不知道为什么就快了很多的倍增法

#include <iostream>
#include <cstdio>
#include <cstring>
#define inv inline void
#define maxN 1000010
using namespace std;
char s[maxN];
//s是字符串的读入
int a[maxN],rk[maxN],sa[maxN],tp[maxN],tax[maxN],n,m;
//a是暂存数组，rk（第一关键字）第i位的排名，sa是排名为i的位置，tp是第二关键字辅助用的，tax是桶数组；
inv read(){
    scanf("%s",&s);
    n=strlen(s);
    for(int i=0;i<n;i++) a[i+1]=s[i];
    //读入
}
inv Rsort(){
    for(int i=0;i<=m;i++) tax[i]=0;
    //tax是桶
    //tax清零
    for(int i=1;i<=n;i++) tax[rk[tp[i]]]++;
    //每一个出现的第一关键字++
    for(int i=1;i<=m;i++) tax[i]+=tax[i-1];
    //tax中i现在代表这个数至多能排第几位
    for(int i=n;i>=1;i--) sa[tax[rk[tp[i]]]--]=tp[i];
    //如果是第一遍就先不看这个
    //就是把这一轮的sa做出来
    //第二轮开始因为tp是按第二关键字进数组的
    //所以从后往前来第二关键字肯定比前面小
    //所以第一关键字相同时，第二关键字越大排名越后
    //所以先拿到最大的值然后--
}
inv Suffix(){
    for(int i=1;i<=n;i++) rk[i]=a[i],tp[i]=i;
    //因为是第一轮所以直接用ascii码和位置当关键字；
    Rsort();
//  for(int i=1;i<=n;i++) printf("%d ",sa[i]);
    for(int k=1;k<=n;k<<=1){
        int num;
        num=0;
        for(int i=n-k+1;i<=n;i++) tp[++num]=i;
        //从n-k+1开始，到n的位置的第二关键字都为零，所以先入数组
        for(int i=1;i<=n;i++) if(sa[i]>k) tp[++num]=sa[i]-k;
        //因为sa是排好序的，当sa[i]这个位置大于k时
        //sa[i]就会作为别人的第二关键字，因为sa排好序的所以从小往大一个for就ok
        //所以就把sa[i]-k这个位置先进
        //上面这两个for做完后tp就完成了
        Rsort();
        //再进行一次基数排序
        swap(rk,tp);
        //用tp存下这一轮rk
        //下面开始更新下一轮rk
        rk[sa[1]]=1;
        //sa[1]的rk就是1
        num=1;
        //计数器&&自带更新排名
        for(int i=2;i<=n;i++)
          rk[sa[i]]=(tp[sa[i]]==tp[sa[i-1]]&&tp[sa[i]+k]==tp[sa[i-1]+k])?num:++num;
          //（）里面的是比较第一和第二关键字是否相同
          //（）里面的如果成立，就直接等于num
          //如果不成立就++num并变成num++
        if(num==n) break;
        //如果有n种排名就done了！
        m=num;
        //m代表tp的种类
    }
    return;
}
int main(){
    freopen("data.in","r",stdin);
    freopen("data.out","w",stdout);

    read();
    m=122;
    Suffix();
    for(int i=1;i<=n;i++) printf("%d ",sa[i]);
//  printf("\n");
//  for(int i=1;i<=n;i++) printf("%d ",rk[i]);
}

DC3

/*
suffix数组：第i位到最后的字符串
sa数组：将排序后的后缀的开头位置顺次放入SA中，称为后缀数组
rank数组：令rank[i]保存suffix[i]在排序中的名次，名次数组
*/
#include "stdio.h"
#include "string.h"
#define maxn 20004
#define maxm 1000005
 
#define F(x) ((x)/3+((x)%3==1?0:tb))
#define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2)
int wa[maxn],wb[maxn],wv[maxn],ws[maxm];
int c0(int *r,int a,int b)
{return r[a]==r[b]&&r[a+1]==r[b+1]&&r[a+2]==r[b+2];}
int c12(int k,int *r,int a,int b)
{if(k==2) return r[a]<r[b]||r[a]==r[b]&&c12(1,r,a+1,b+1);
 else return r[a]<r[b]||r[a]==r[b]&&wv[a+1]<wv[b+1];}
void sort(int *r,int *a,int *b,int n,int m)
{
     int i;
     for(i=0;i<n;i++) wv[i]=r[a[i]];
     for(i=0;i<m;i++) ws[i]=0;
     for(i=0;i<n;i++) ws[wv[i]]++;
     for(i=1;i<m;i++) ws[i]+=ws[i-1];
     for(i=n-1;i>=0;i--) b[--ws[wv[i]]]=a[i];
     return;
}
void dc3(int *r,int *sa,int n,int m)
{
     int i,j,*rn=r+n,*san=sa+n,ta=0,tb=(n+1)/3,tbc=0,p;
     r[n]=r[n+1]=0;
     for(i=0;i<n;i++) if(i%3!=0) wa[tbc++]=i;
     sort(r+2,wa,wb,tbc,m);
     sort(r+1,wb,wa,tbc,m);
     sort(r,wa,wb,tbc,m);
     for(p=1,rn[F(wb[0])]=0,i=1;i<tbc;i++)
     rn[F(wb[i])]=c0(r,wb[i-1],wb[i])?p-1:p++;
     if(p<tbc) dc3(rn,san,tbc,p);
     else for(i=0;i<tbc;i++) san[rn[i]]=i;
     for(i=0;i<tbc;i++) if(san[i]<tb) wb[ta++]=san[i]*3;
     if(n%3==1) wb[ta++]=n-1;
     sort(r,wb,wa,ta,m);
     for(i=0;i<tbc;i++) wv[wb[i]=G(san[i])]=i;
     for(i=0,j=0,p=0;i<ta && j<tbc;p++)
     sa[p]=c12(wb[j]%3,r,wa[i],wb[j])?wa[i++]:wb[j++];
     for(;i<ta;p++) sa[p]=wa[i++];
     for(;j<tbc;p++) sa[p]=wb[j++];
     return;
}
int rank[maxn],height[maxn];
void calheight(int *r,int *sa,int n)
{
     int i,j,k=0;
     for(i=1;i<=n;i++) rank[sa[i]]=i;
     for(i=0;i<n;height[rank[i++]]=k)
     for(k?k--:0,j=sa[rank[i]-1];r[i+k]==r[j+k];k++);
     return;
}
int RMQ[maxn];
int mm[maxn];
int best[20][maxn];
void initRMQ(int n)
{
     int i,j,a,b;
     for(mm[0]=-1,i=1;i<=n;i++)
     mm[i]=((i&(i-1))==0)?mm[i-1]+1:mm[i-1];
     for(i=1;i<=n;i++) best[0][i]=i;
     for(i=1;i<=mm[n];i++)
     for(j=1;j<=n+1-(1<<i);j++)
     {
       a=best[i-1][j];
       b=best[i-1][j+(1<<(i-1))];
       if(RMQ[a]<RMQ[b]) best[i][j]=a;
       else best[i][j]=b;
     }
     return;
}
int askRMQ(int a,int b)
{
    int t;
    t=mm[b-a+1];b-=(1<<t)-1;
    a=best[t][a];b=best[t][b];
    return RMQ[a]<RMQ[b]?a:b;
}
int lcp(int a,int b)//从头开始比较a和b的对应字符持续相等的最远值
{
    int t;
    a=rank[a];b=rank[b];
    if(a>b) {t=a;a=b;b=t;}
    return(height[askRMQ(a+1,b)]);
}
/*
*/
char st[maxn];
int r[maxn*3],sa[maxn*3];
/*求最长回文长
int main()
{
    int i,n,len,k,ans=0,w;
    scanf("%s",st);
    len=strlen(st);
    for(i=0;i<len;i++) r[i]=st[i];
    r[len]=1;
    for(i=0;i<len;i++) r[i+len+1]=st[len-1-i];
    n=len+len+1;
    r[n]=0;
    dc3(r,sa,n+1,128);
    calheight(r,sa,n);
    for(i=1;i<=n;i++) RMQ[i]=height[i];
    initRMQ(n);
    for(i=0;i<len;i++)
    {
      k=lcp(i,n-i);
      if(k*2>ans) ans=k*2,w=i-k;
      k=lcp(i,n-i-1);
      if(k*2-1>ans) ans=k*2-1,w=i-k+1;
    }
    st[w+ans]=0;
    printf("%s\n",st+w);
    return 0;
}*/
/*求最大公共字串长
int main()
{
    int i,j,n,ans=0;
    scanf("%s",st);
    j=strlen(st);
    st[j]=1;
    scanf("%s",st+j+1);
    n=strlen(st);
    for(i=0;i<n;i++) r[i]=st[i];
    r[n]=0;
    dc3(r,sa,n+1,128);
    calheight(r,sa,n);
    for(i=2;i<=n;i++)
    if(height[i]>ans)
    if((j<sa[i-1] && j>sa[i])
    || (j>sa[i-1] && j<sa[i])) ans=height[i];
    printf("%d\n",ans);
    return 0;
}
*/
/*不可重叠最长重复子串
 POJ 1743 最长重复子串（不可重叠）
题意：
有N(1 <= N <=20000)个音符的序列来表示一首乐曲，每个音符都是1..88范围内的整数，现在要找一个重复的主题。“主题”是整个音符序列的一个子串，它需要满足如下条件：
1.长度至少为5个音符
2.在乐曲中重复出现(可能经过转调，“转调”的意思是主题序列中每个音符都被加上或减去了同一个整数值。)
3.重复出现的同一主题不能有公共部分。
int check(int *sa,int n,int k)
{
    int i,max=sa[1],min=sa[1];
    for(i=2;i<=n;i++)
    {
      if(height[i]<k) max=min=sa[i];
      else
      {
        if(sa[i]<min) min=sa[i];
        if(sa[i]>max) max=sa[i];
        if(max-min>k) return(1);
      }
    }
    return(0);
}
int main()
{
    int i,j=0,k,n;
    int min,mid,max;
    scanf("%d",&n);
    while(n!=0)
    {
      n--;
      for(i=0;i<n;i++)
        scanf("%d",&r[i]);
      for(i=0;i<n;i++)
       r[i]=r[i]-r[i+1]+90;
      r[n]=0;
      dc3(r,sa,n+1,200);
      calheight(r,sa,n);
      min=1;max=n/2;
      while(min<=max)
      {
        mid=(min+max)/2;
        if(check(sa,n,mid)) min=mid+1;
        else max=mid-1;
      }
      if(max>=4) printf("%d\n",max+1);
      else printf("0\n");
      scanf("%d",&n);
    }
    return 0;
}
*/
/*
可重叠的 k 次最长重复子串
给定一个长度为n的整数序列，求其中至少出现k次的子序列长度最长为多长
int check(int n,int k,int mid)
{
    int i,s=1;
    for(i=1;i<=n;i++)
    if(height[i]>=mid)
    {
      s++;
      if(s>=k) return(1);
    }
    else s=1;
    return(0);
}
int main()
{
    int i,k,n;
    int min,mid,max;
    scanf("%d %d",&n,&k);
    for(i=0;i<n;i++)
    {
      scanf("%d",&r[i]);
      r[i]++;
    }
    r[n]=0;
    dc3(r,sa,n+1,1000002);
    calheight(r,sa,n);
    min=1;max=n;
    while(min<=max)
    {
      mid=(min+max)/2;
      if(check(n,k,mid)) min=mid+1;
      else max=mid-1;
    }
    printf("%d\n",max);
    return 0;
}
*/
 
/*
不相同的连续子串的个数
int main()
{
    int i,n,t,ans;
    scanf("%d",&t);
    while(t-->0)
    {
      scanf("%s",st);
      n=strlen(st);
      for(i=0;i<n;i++) r[i]=st[i];
      r[n]=0;
      dc3(r,sa,n+1,128);
      calheight(r,sa,n);
      ans=n*(n+1)/2;
      for(i=1;i<=n;i++) ans-=height[i];
      printf("%d\n",ans);
    }
    return 0;
}
*/
/*
长度不小于 k 的公共子串的个数
int f[maxn];
int a[maxn],b[maxn],c;
long long ss,ans;
int main()
{
    int i,k,l,n,t;
    scanf("%d",&k);
    while(k!=0)
    {
      scanf("%s",st);
      l=strlen(st);
      st[l]=1;
      scanf("%s",st+l+1);
      n=strlen(st);
      for(i=0;i<n;i++) r[i]=st[i];
      r[n]=0;
      dc3(r,sa,n+1,128);
      calheight(r,sa,n);
      for(i=2;i<=n;i++)
      {
        f[i]=sa[i]<l;
        height[i]-=k-1;
        if(height[i]<0) height[i]=0;
      }
      height[n+1]=0;
      a[0]=-1;ans=0;
      for(t=0;t<=1;t++)
      for(c=0,ss=0,i=2;i<=n;i++)
      {
        if(f[i]!=t) ans+=ss;
        c++;
        a[c]=height[i+1];
        b[c]=f[i]==t;
        ss+=(long long)a[c]*b[c];
        while(a[c-1]>=a[c])
        {
          ss-=(long long)(a[c-1]-a[c])*b[c-1];
          a[c-1]=a[c];
          b[c-1]+=b[c];
          c--;
        }
      }
      printf("%I64d\n",ans);
      scanf("%d",&k);
    }
    return 0;
}
*/
 

 7.4 KMP

#include <bits/stdc++.h>
using namespace std;

const int maxn=1e6+7;
int Next[maxn];
//x表示模式串，Next保存以i为结尾的最长公共前缀和后缀的起始坐标
void get_next(string x){
    int i,j;
    Next[0]=j=-1;
    i=0;
    while(i<x.length()){
        while(j!=-1&&x[j]!=x[i])j=Next[j];
        Next[++i]=++j;
    }
}
//返回第一次匹配下标，x1匹配串,x2模式串
int kmp_id(string x1,string x2){
    int i,j;
    i=j=0;
    while(i<x1.length()&&j<x2.length()){
        while(j!=-1&&x1[i]!=x2[j]){
            j=Next[j];
        }
        i++;
        j++;
    }
    if(j==x2.length())
        return i-j;
    return -1;
}

//返回匹配次数，x1匹配串,x2模式串
int kmp_ans(string x1,string x2){
    int i,j;
    i=j=0;
    int ans=0;
    while(i<x1.length()){
        while(j!=-1&&x1[i]!=x2[j]){
            j=Next[j];
        }
        if(j==x2.length()-1){
            ans++;
            j=Next[j];
        }
        i++;
        j++;
    }
    return ans;
}


int main()
{
    string x,y;
    cin >> x;
    get_next(x);
    cin >>y;
    cout <<  kmp_ans(y,x) << endl;
    cout <<  kmp_id(y,x) << endl;

    return 0;
}

 

void get_next()
{//next数组保存了以i结尾的字符串的最长公共前缀和后缀的起始坐标
    int i,j;
    next[0] = j = -1;
    i = 0;
    while(i < l2)
    {
        while(j!=-1&&str2[j]!=str2[i])//自身和自身进行匹配
            j = next[j];
        next[++i] = ++j; 
    }
}
int kmp()
{
    int i,j;
    i = j = 0;
    while(i < l1&&j<l2)
    {
        while(j!=-1&&str1[i]!=str2[j])
        {
            j = next[j];
        }
        i++;
        j++;

    }
    if(j == l2)
        return i-j;//完全匹配时的开始下标，下标从0开始
    return -1;//不存在匹配情况 
}
int kmp()
{
    int i,j;
    i = j = 0;
    while(i < l1)//注意和返回下标的区别
    {
        while(j!=-1&&str1[i]!=str2[j])
        {
            j = next[j];
        }
        if(j == l2-1)
        {
           ans ++;
           j = next[j];
        }
        i++;
        j++;
    }
    return ans;//返回匹配次数 
}

void getnext( char T[],int len)
{
    int i = 0, j = -1;
    Next[0] = -1;
    while(i < len)
    {
        if(j == -1 || T[i] == T[j])
        {
            i++,j++;
            Next[i] = j;
        }
        else
            j = Next[j];
    }
}
 
void KMP(char s1[], char s2[], int len1, int len2 )//原串长度， 模式串长度
{
    int i = 0, j = 0 ;
    Next[0] = -1 ;
    while( i < len1 && j < len2 )
    {
        if( j == -1 || s1[i] == s2[j])
        {
            i++;
            j++;
        }
        else
            j = Next[j];
        if( j == len2)
        {
            if(i < len1)
            {
                ans = min(ans, len1 - i);
            }
            j = Next[j];
        }
    }
}

7.5 字典树

#include <cstring>
#include <vector>
#include <cstdio>
using namespace std;
//***********************************************************************************************
const int maxnode = 4000 * 100 + 10;
const int sigma_size = 26;
 
// 字母表为全体小写字母的Trie
struct Trie {
  int ch[maxnode][sigma_size];
  int val[maxnode];
  int sz; // 结点总数
  void clear() { sz = 1; memset(ch[0], 0, sizeof(ch[0])); } // 初始时只有一个根结点
  int idx(char c) { return c - 'a'; } // 字符c的编号
 
  // 插入字符串s，附加信息为v。注意v必须非0，因为0代表“本结点不是单词结点”
  void insert(const char *s, int v) {
    int u = 0, n = strlen(s);
    for(int i = 0; i < n; i++) {
      int c = idx(s[i]);
      if(!ch[u][c]) { // 结点不存在
        memset(ch[sz], 0, sizeof(ch[sz]));
        val[sz] = 0;  // 中间结点的附加信息为0
        ch[u][c] = sz++; // 新建结点
      }
      u = ch[u][c]; // 往下走
    }
    val[u] = v; // 字符串的最后一个字符的附加信息为v
  }
 
  // 找字符串s的长度不超过len的前缀
  bool find(const char *s, int len) {
    int u = 0;
    for(int i = 0; i < len; i++) {
      if(s[i] == '\0') break;
      int c = idx(s[i]);
      if(!ch[u][c]) break;
      u = ch[u][c];
      if(val[u] != 0) return true; // 找到一个前缀
    }
    return false;
  }
};
 
//*****************************************************************************************************
//以下为模板测试
Trie trie;
const int maxl = 300000 + 10; // 文本串最大长度
const int maxw = 4000 + 10;   // 单词最大个数
const int maxwl = 100 + 10;   // 每个单词最大长度
char text[maxl], word[maxwl];
int main()
{
    int n,m;
    scanf("%d",&n);
    trie.clear();
    while(n--){
        scanf("%s",word);
        trie.insert(word,1);
    }
    scanf("%d",&m);
    while(m--){
        scanf("%s",text);
        int l=strlen(text);
        if(trie.find(text,l)) printf("\"%s\" in it\n",text);
        else printf("\"%s\" not in it\n",text);
    }
    return 0;
}

 

//Code highlighting produced by Actipro CodeHighlighter //(freeware)http://www.CodeHighlighter.com/-->
void createTrie(char *str)
{
    int len = strlen(str);
    Trie *p = root, *q;
    for(int i=0; i<len; ++i)
    {
        int id = str[i]-'0';
        if(p->next[id] == NULL)
        {
            q = (Trie *)malloc(sizeof(Trie));
            q->v = 1;    //初始v==1
            for(int j=0; j<MAX; ++j)
                q->next[j] = NULL;
            p->next[id] = q;
            p = p->next[id];
        }
        else
        {
            p->next[id]->v++;
            p = p->next[id];
        }
    }
    p->v = -1;   //若为结尾，则将v改成-1表示
}

//Code highlighting produced by Actipro CodeHighlighter //(freeware)http://www.CodeHighlighter.com/-->
int findTrie(char *str)
{
    int len = strlen(str);
    Trie *p = root;
    for(int i=0; i<len; ++i)
    {
        int id = str[i]-'0';
        p = p->next[id];
        if(p == NULL)   //若为空集，表示不存以此为前缀的串
            return 0;
        if(p->v == -1)   //字符集中已有串是此串的前缀
            return -1;
    }
    return -1;   //此串是字符集中某串的前缀
}

//Code highlighting produced by Actipro CodeHighlighter //(freeware)http://www.CodeHighlighter.com/-->
int dealTrie(Trie* T)
{
    int i;
    if(T==NULL)
        return 0;
    for(i=0;i<MAX;i++)
    {
        if(T->next[i]!=NULL)
            deal(T->next[i]);
    }
    free(T);
    return 0;
}

#include <cstring>
#include <vector>
#include <cstdio>
using namespace std;
//***********************************************************************************************
const int maxnode = 4000 * 100 + 10;
const int sigma_size = 26;
 
// 字母表为全体小写字母的Trie
struct Trie {
  int ch[maxnode][sigma_size];
  int val[maxnode];
  int sz; // 结点总数
  void clear() { sz = 1; memset(ch[0], 0, sizeof(ch[0])); } // 初始时只有一个根结点
  int idx(char c) { return c - 'a'; } // 字符c的编号
 
  // 插入字符串s，附加信息为v。注意v必须非0，因为0代表“本结点不是单词结点”
  void insert(const char *s, int v) {
    int u = 0, n = strlen(s);
    for(int i = 0; i < n; i++) {
      int c = idx(s[i]);
      if(!ch[u][c]) { // 结点不存在
        memset(ch[sz], 0, sizeof(ch[sz]));
        val[sz] = 0;  // 中间结点的附加信息为0
        ch[u][c] = sz++; // 新建结点
      }
      u = ch[u][c]; // 往下走
    }
    val[u] = v; // 字符串的最后一个字符的附加信息为v
  }
 
  // 找字符串s的长度不超过len的前缀
  bool find(const char *s, int len) {
    int u = 0;
    for(int i = 0; i < len; i++) {
      if(s[i] == '\0') break;
      int c = idx(s[i]);
      if(!ch[u][c]) break;
      u = ch[u][c];
      if(val[u] != 0) return true; // 找到一个前缀
    }
    return false;
  }
};
 
//*****************************************************************************************************
//以下为模板测试
Trie trie;
const int maxl = 300000 + 10; // 文本串最大长度
const int maxw = 4000 + 10;   // 单词最大个数
const int maxwl = 100 + 10;   // 每个单词最大长度
char text[maxl], word[maxwl];
int main()
{
    int n,m;
    scanf("%d",&n);
    trie.clear();
    while(n--){
        scanf("%s",word);
        trie.insert(word,1);
    }
    scanf("%d",&m);
    while(m--){
        scanf("%s",text);
        int l=strlen(text);
        if(trie.find(text,l)) printf("\"%s\" in it\n",text);
        else printf("\"%s\" not in it\n",text);
    }
    return 0;
}

 

7.6 AC自动机

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>

using namespace std;

const int maxn=550000;

struct AC_auto
{
    //chd子节点 v表示字符长度，f表示失配指针，
    int chd[maxn][26],v[maxn],f[maxn],last[maxn],sz,ans;
    void init()
    {
        sz=1;ans=0;
        memset(v,0,sizeof(v));
        memset(f,0,sizeof(f));
        memset(chd[0],0,sizeof(chd[0]));
    }
    void insert(char* p)
    {
        int cur=0;
        int tmp=strlen(p);
        for(;*p;p++)
        {
            if(!chd[cur][*p-'a'])
            {
                memset(chd[sz],0,sizeof(chd[sz]));
                chd[cur][*p-'a']=sz++;
            }
            cur=chd[cur][*p-'a'];
        }
        v[cur]=tmp;
    }
    bool query(char* p)
    {
        int cur=0;
        for(;*p;p++)
        {
            if(!chd[cur][*p-'a']) break;
            cur=chd[cur][*p-'a'];
        }
        return v[cur]&&(!(*p));
    }
    int getFail()
    {
        queue<int> q;
        f[0]=0;
        for(int c=0;c<26;c++)
        {
            int u=chd[0][c];
            if(u)
            {
                f[u]=0; q.push(u); last[u]=0;
            }
        }
        while(!q.empty())
        {
            int r=q.front(); q.pop();
            for(int c=0;c<26;c++)
            {
                int u=chd[r][c];
                if(!u){ chd[r][c]=chd[f[r]][c];continue;}///....
                q.push(u);
                int vv=f[r];
                while(vv&&!chd[vv][c]) vv=f[vv];
                f[u]=chd[vv][c];
                last[u]=v[f[u]] ? f[u] : last[f[u]];
            }
        }
    }
    void solve(int j)
    {
        if(!j) return;
        if(v[j])
        {
            ans+=v[j];
            v[j]=0;
        }
        solve(last[j]);
    }
    //找出现单词（不计次数）
    void find(char* T)
    {
        int n=strlen(T),j=0;
        getFail();
        for(int i=0;i<n;i++)
        {
            //while(j&&!chd[j][*T-'a']) j=f[j];
            j=chd[j][T[i]-'a'];
            if(v[j]) solve(j);
            else if(last[j]) solve(last[j]);
        }
    }
    //替换最长匹配前缀为'*';
    void find1(char* T)
    {
        int n=strlen(T),j=0;
        getFail();
        for(int i=0; i<n; i++)
        {
//            if(!(str[i]>='a'&&str[i]<='z'||str[i]>='A'&&str[i]<='Z'))continue;


            j=chd[j][T[i]-'a'];
            int temp=j;
            while(temp!=0)
            {
                if(v[temp] != 0)
                {
                    for(int k=i-v[temp]+1; k<=i; k++)
                    {
                        //str1[k]='*';
                    }
                    break;
                }
                temp = f[temp];
            }


        }
    }
}ac;

int main()
{
    int t,n;
    char dic[100],str[1100000];
    scanf("%d",&t);
    while(t--)
    {
        ac.init();
        scanf("%d",&n);
        while(n--)
        {
            scanf("%s",dic);
            ac.insert(dic);
        }
        scanf("%s",str);
        ac.find(str);
        printf("%d\n",ac.ans);
    }
    return 0;
}

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
 
using namespace std;
 
const int maxn=550000;
 
struct AC_auto
{
    int chd[maxn][26],v[maxn],f[maxn],last[maxn],sz,ans;
    void init()
    {
        sz=1;ans=0;
        memset(v,0,sizeof(v));
        memset(f,0,sizeof(f));
        memset(chd[0],0,sizeof(chd[0]));
    }
    void insert(char* p)
    {
        int cur=0;
        for(;*p;p++)
        {
            if(!chd[cur][*p-'a'])
            {
                memset(chd[sz],0,sizeof(chd[sz]));
                chd[cur][*p-'a']=sz++;
            }
            cur=chd[cur][*p-'a'];
        }
        v[cur]++;
    }
    bool query(char* p)
    {
        int cur=0;
        for(;*p;p++)
        {
            if(!chd[cur][*p-'a']) break;
            cur=chd[cur][*p-'a'];
        }
        return v[cur]&&(!(*p));
    }
    int getFail()
    {
        queue<int> q;
        f[0]=0;
        for(int c=0;c<26;c++)
        {
            int u=chd[0][c];
            if(u)
            {
                f[u]=0; q.push(u); last[u]=0;
            }
        }
        while(!q.empty())
        {
            int r=q.front(); q.pop();
            for(int c=0;c<26;c++)
            {
                int u=chd[r][c];
                if(!u){ chd[r][c]=chd[f[r]][c];continue;}///....
                q.push(u);
                int vv=f[r];
                while(vv&&!chd[vv][c]) vv=f[vv];
                f[u]=chd[vv][c];
                last[u]=v[f[u]] ? f[u] : last[f[u]];
            }
        }
    }
    void solve(int j)
    {
        if(!j) return;
        if(v[j])
        {
            ans+=v[j];
            v[j]=0;
        }
        solve(last[j]);
    }
    void find(char* T)
    {
        int n=strlen(T),j=0;
        getFail();
        for(int i=0;i<n;i++)
        {
            //while(j&&!chd[j][*T-'a']) j=f[j];
            j=chd[j][T[i]-'a'];
            if(v[j]) solve(j);
            else if(last[j]) solve(last[j]);
        }
    }
}ac;
 
int main()
{
    int t,n;
    char dic[100],str[1100000];
    scanf("%d",&t);
    while(t--)
    {
        ac.init();
        scanf("%d",&n);
        while(n--)
        {
            scanf("%s",dic);
            ac.insert(dic);
        }
        scanf("%s",str);
        ac.find(str);
        printf("%d\n",ac.ans);
    }
    return 0;
}

 7.7 扩展KMP

#include <bits/stdc++.h>
using namespace std;
//const int maxn=1e5+10;
//int Next[maxn];
//int ret[maxn];
//
////扩展kmp求a为模式串，b为文本串的，b的所有后缀对a的最长公共前缀
//void extendedKMP(char *a,char *b,int M,int N,int *Next,int *ret){
//    int i,j,k;
//    for(j=0;1+j<M&&a[j]==a[1+j];j++);
//    Next[1]=j;
//    k=1;
//    for(i=2;i<M;i++){
//        int Len=k+Next[k],L=Next[i-k];
//        if(L<Len-i){
//            Next[i]=L;
//        }else {
//            for(j=max(0,Len-i);i+j<M&&a[j]==a[i+j];j++);
//            Next[i]=j;
//            k=i;
//        }
//    }
//
//    for(j=0;j<N&&j<M&&a[j]==b[j];j++);
//    ret[0]=j;
//    k=0;
//    for(i=1;i<N;i++){
//        int Len=k+ret[k],L=Next[i-k];
//        if(L<Len-i){
//            ret[i]=L;
//        }else {
//            for(i=max(0,Len-i);j<M&&i+j<N&&a[j]==b[i+j];j++);
//            ret[i]==j;k=i;
//        }
//    }
//
//}
const int maxn=100010;   //字符串长度最大值
int next[maxn],ex[maxn]; //ex数组即为extend数组
//预处理计算next数组
void GETNEXT(char *str)
{
    int i=0,j,po,len=strlen(str);
    next[0]=len;//初始化next[0]
    while(str[i]==str[i+1]&&i+1<len)//计算next[1]
    i++;
    next[1]=i;
    po=1;//初始化po的位置
    for(i=2;i<len;i++)
    {
        if(next[i-po]+i<next[po]+po)//第一种情况，可以直接得到next[i]的值
        next[i]=next[i-po];
        else//第二种情况，要继续匹配才能得到next[i]的值
        {
            j=next[po]+po-i;
            if(j<0)j=0;//如果i>po+next[po],则要从头开始匹配
            while(i+j<len&&str[j]==str[j+i])//计算next[i]
            j++;
            next[i]=j;
            po=i;//更新po的位置
        }
    }
}
//计算extend数组,s1为文本串，s2为模式串，求s1的所有后缀对s2的最长公共前缀
void EXKMP(char *s1,char *s2)
{
    int i=0,j,po,len=strlen(s1),l2=strlen(s2);
    GETNEXT(s2);//计算子串的next数组
    while(s1[i]==s2[i]&&i<l2&&i<len)//计算ex[0]
    i++;
    ex[0]=i;
    po=0;//初始化po的位置
    for(i=1;i<len;i++)
    {
        if(next[i-po]+i<ex[po]+po)//第一种情况，直接可以得到ex[i]的值
        ex[i]=next[i-po];
        else//第二种情况，要继续匹配才能得到ex[i]的值
        {
            j=ex[po]+po-i;
            if(j<0)j=0;//如果i>ex[po]+po则要从头开始匹配
            while(i+j<len&&j<l2&&s1[j+i]==s2[j])//计算ex[i]
            j++;
            ex[i]=j;
            po=i;//更新po的位置
        }
    }
}

int main()
{
    char *a="aaaabaa";
    char *b="aaaaaaa";
    EXKMP(a,b);
    for(int i=0;i<7;i++){
        printf("%d %d\n",next[i],ex[i]);
    }
}

 

 7.8 华丽的hash

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef unsigned long long ull;
ull base=131;
ull a[10010];
char s[10010];
int n,ans=1;
ull hashs(char s[])
{
    int len=strlen(s);
    ull ans=0;
    for (int i=0;i<len;i++)
        ans=ans*base+(ull)s[i];
    return ans&0x7fffffff;
}
main()
{
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
    {
        scanf("%s",s);
        a[i]=hashs(s);
    }
    sort(a+1,a+n+1);
    for (int i=2;i<=n;i++)
        if (a[i]!=a[i-1])
            ans++;
    printf("%d\n",ans);
}
 

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef unsigned long long ull;
ull base=131;
ull a[10010];
char s[10010];
int n,ans=1;
ull mod=19260817;
ull hashs(char s[])
{
    int len=strlen(s);
    ull ans=0;
    for (int i=0;i<len;i++)
        ans=(ans*base+(ull)s[i])%mod;
    return ans;
}
main()
{
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
    {
        scanf("%s",s);
        a[i]=hashs(s);
    }
    sort(a+1,a+n+1);
    for (int i=2;i<=n;i++)
        if (a[i]!=a[i-1])
            ans++;
    printf("%d\n",ans);
}
 

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef unsigned long long ull;
ull base=131;
struct data
{
    ull x,y;
}a[10010];
char s[10010];
int n,ans=1;
ull mod1=19260817;
ull mod2=19660813;
ull hash1(char s[])
{
    int len=strlen(s);
    ull ans=0;
    for (int i=0;i<len;i++)
        ans=(ans*base+(ull)s[i])%mod1;
    return ans;
}
ull hash2(char s[])
{
    int len=strlen(s);
    ull ans=0;
    for (int i=0;i<len;i++)
        ans=(ans*base+(ull)s[i])%mod2;
    return ans;
}
bool comp(data a,data b)
{
    return a.x<b.x;
}
main()
{
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
    {
        scanf("%s",s);
        a[i].x=hash1(s);
        a[i].y=hash2(s);
    }
    sort(a+1,a+n+1,comp);
    for (int i=2;i<=n;i++)
        if (a[i].x!=a[i-1].x || a[i-1].y!=a[i].y)
            ans++;
    printf("%d\n",ans);
}

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef unsigned long long ull;
ull base=131;
ull a[10010];
char s[10010];
int n,ans=1;
ull mod=212370440130137957ll;
ull hashs(char s[])
{
    int len=strlen(s);
    ull ans=0;
    for (int i=0;i<len;i++)
        ans=(ans*base+(ull)s[i])%mod;
    return ans;
}
main()
{
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
    {
        scanf("%s",s);
        a[i]=hashs(s);
    }
    sort(a+1,a+n+1);
    for (int i=2;i<=n;i++)
        if (a[i]!=a[i-1])
            ans++;
    printf("%d\n",ans);
}

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef unsigned long long ull;
ull base=131;
ull po[100010],hs[100010*100];
char s1[100010],s2[100010*100];
int n,ans=1,T;
ull geth(int l,int r)
{
    return (ull)hs[r]-po[r-l+1]*hs[l-1];
}
main()
{
    freopen("oulipo.in","r",stdin);
    freopen("oulipo.out","w",stdout);
    po[0]=1;
    for (int i=1;i<=10010-5;i++)
        po[i]=po[i-1]*base;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%s%s",s1+1,s2+1);
        int l1=strlen(s1+1),l2=strlen(s2+1);
        ull a1=0,ans=0;
        for (int i=1;i<=l1;i++)
            a1=a1*base+(ull)s1[i];
        for (int i=1;i<=l2;i++)
            hs[i]=hs[i-1]*base+s2[i];
        for (int i=1;i+l1-1<=l2;i++)
            if (a1==geth(i,i+l1-1))
                ans++;
        printf("%d\n",ans);
    }
}

写到这里突然发现hash好像可以暴力水过很多字符串算法。。

1、kmp

问题：给两个字符串S1，S2，求S2是否是S1的子串，并求S2在S1中出现的次数

把S2 Hash出来，在S1里找所有长度为|S2||S2|的子串，Hash比较。效率O(|S1|)O(|S1|)

2、AC自动机

问题：给N个单词串，和一个文章串，求每个单词串是否是文章串的子串，并求每个单词在文章中出现的次数。

把每一个单词hash成整数，再把文章的每一个子串hash成整数，接下来只需要进行整数上的查找即可。

复杂度：O(|A|2+|S|)O(|A|2+|S|)

用AC自动机可以做到O(|A|+|S|)O(|A|+|S|)的复杂度,|S||S|是单词串总长，|A||A|是文章长度

3、后缀数组

问题：给两个字符串S1,S2，求它们的最长公共子串的长度。

将S1的每一个子串都hash成一个整数，将S2的每一个子串都hash成一个整数

两堆整数，相同的配对，并且找到所表示的字符串长度最大的即可。

复杂度：O(|S1|2+|S2|2)O(|S1|2+|S2|2)

用后缀数组可以优化到O(|S|log|S|)O(|S|log|S|)

4、马拉车

问题：给一个字符串S，求S的最长回文子串。

先求子串长度位奇数的，再求偶数的。枚举回文子串的中心位置，然后二分子串的长度，直到找到一个该位置的最长回文子串，不断维护长度最大值即可。

复杂度：O(|S|log|S|)O(|S|log|S|)

用manacher可以做到O(|S|)O(|S|)的复杂度

5、扩展kmp

问题：给一个字符串S，求S的每个后缀与S的最长公共前缀

枚举每一个后缀的起始位置，二分长度，求出每个后缀与S的最长公共前缀。

复杂度：O(|S|log|S|)O(|S|log|S|)

用extend-kmp可以做到O(|S|)

 

 

八、杂

8.1 三分求极大极小点

int SanFen(int l,int r) //找凸点  
{  
    while(l < r-1)  
    {  
        int mid  = (l+r)/2;  
        int mmid = (mid+r)/2;  
        if( f(mid) > f(mmid) )  
            r = mmid;  
        else  
            l = mid;  
    }  
    return f(l) > f(r) ? l : r;  
}  

double three_devide(double low,double up)  
{  
    double m1,m2;  
    while(up-low>=eps)  
    {  
        m1=low+(up-low)/3;  
        m2=up-(up-low)/3;  
        if(f(m1)<=f(m2))  
            low=m1;  
        else  
            up=m2;  
    }  
    return (m1+m2)/2;  
}  

int SanFen(int l,int r) //找凸点  
{  
    while(l < r-1)  
    {  
        int mid  = (l+r)/2;  
        int mmid = (mid+r)/2;  
        if( f(mid) > f(mmid) )  
            l = mid;  
        else  
            r = mmid;  
    }  
    return f(l) > f(r) ? l : r;  
}  

double three_devide(double low,double up)  
{  
    double m1,m2;  
    while(up-low>=eps)  
    {  
        m1=low+(up-low)/3;  
        m2=up-(up-low)/3;  
        if(f(m1)<=f(m2))  
            up=m2;  
        else  
            low=m1;  
    }  
    return (m1+m2)/2;  
}  

 8.2 欧拉函数递推

void Euler(){
    phi[1] = 1;
    for(int i = 2; i < N; i ++){
        if(!phi[i]){
            phi[i] = i-1;
            prime[tot ++] = i;
        }
        for(int j = 0; j < tot && 1ll*i*prime[j] < N; j ++){
            if(i % prime[j]) phi[i * prime[j]] = phi[i] * (prime[j]-1);
            else{
                phi[i * prime[j] ] = phi[i] * prime[j];
                break;
            }
        }
    }
    sum[1]=0;
    for(int i=2;i<N/2;i++){
        sum[i]=phi[2*i]/2;
        sum[i]=sum[i-1]+sum[i];
    }
}