复健训练-CF gym103495部分
【这场是一个校内训练赛搬来的题】
【纪念一下,把所有题订完了】
【以及,这场训练赛中拿了人生第一个first blood > < ,虽然说那个 C 题要是早点发现错误就会有两个了,【呜呜,可能觉得我拿了一个就会骄傲,就不给我第二个了...】
A. Spring Couplets
题意:给你一对春联,给出声调,问你这副春联是否平仄相对,平仄相对的规定是,前面 n-1 个字,上联是平/仄声下联就要是仄/平声,最后一个字必须上联是仄下联是平。平声是 1 2 声,仄声是 3 4 声。(论语文素养的重要性..
做法:看懂题意是关键(直接做就好了

#include<bits/stdc++.h> #define rep(i,x,y) for (int i=(x);i<=(y);i++) #define ll long long using namespace std; const int N = 1005; int n, a[N], b[N]; char s[N]; void Main(){ scanf("%d", &n); rep (i,1,n){ scanf("%s", s+1); int l = strlen(s+1); a[i]=s[l]-'0'; } rep (i,1,n){ scanf("%s", s+1); int l = strlen(s+1); b[i]=s[l]-'0'; } rep (i,1,n-1){ if (!(a[i]<=2 && b[i]>=3 || (a[i]>=3 && b[i]<=2))) {puts("NO"); return;} } if (!(a[n]>=3 && b[n]<=2)){puts("NO"); return;} puts("YES"); return; } int main(){ int T; scanf("%d", &T); while (T--) Main(); return 0; }
B. Among Us
题意:给一张无向图,现在有两个猎人和 k 个猎物,已知 E 个规则,每个规则会告诉你 $p_i$ 这个猎物会在 $x_i$ 点处,在 $t_i$ 的时间出现。猎人可以选择两个动作,一是沿着一条边走到另一个点,花费时间为边权;二是呆在原地等待。如果猎人在的这个点,当前时间恰好有猎物出现,他就可以把该猎物杀掉。现在两个猎人要把所有猎物杀掉,总时间不能超过 $tmax$ ,问最少时间是多少?$n\le 10^4,m\le 2\times 10^4,E\le 10^5,k\le 8$
做法:【题意真的好难读啊...】这个数据范围明显是要状压的。显然可以把两个起点分开考虑,然后状压 dp ,$dp[s][i]$ 表示当前状态是 s ,走到点 i 的最少时间,状态就是抓了哪些猎物。每次转移有两种,第一种是走边,对于这个 s 跑一个最短路即可。第二种是原地转移,就是枚举当前要等待的猎物,当前时间就变成这个猎物的出现时间。最后对于两个起点进行合并,具体可以看代码。
【这个题一开始想法是直接拆点跑 dijkstra ,但是这样好像会 T (自己没试过 > < 大佬讲的),因为第二种转移 E 的范围有$10^5$ ,所以第二种转移边数大概有 $E\times 2^k$ ,dijkstra 的复杂度是 $m \log m$ ,这样算一下复杂度直接爆了,所以不能直接这么多,要按照状态来 dp 】

#include<bits/stdc++.h> #define rep(i,x,y) for (int i=(x);i<=(y);i++) #define pii pair<int,int> #define fi first #define se second using namespace std; const int N = 1e4+10, M = 2e4+10, S = 260; const int inf = 1e9; int n, m, K, E, s1, s2, cnt, tmax, head[N], dp1[S][N], dp2[S][N], ans1[S], ans2[S], vis[N], ans; struct edge{ int to, nxt, w; }e[M<<1]; vector<pii> V[N]; void adde(int x,int y,int w){ e[++cnt].to=y; e[cnt].nxt=head[x]; head[x]=cnt; e[cnt].w=w; } priority_queue<pii, vector<pii>, greater<pii> > q; void trans(int s, int dp[S][N]){ rep (i,1,n) q.push(pii(dp[s][i], i)), vis[i] = 0; while (!q.empty()){ int u = q.top().se; q.pop(); vis[u] = 1; for (int i=head[u]; i; i=e[i].nxt){ int v = e[i].to; if (dp[s][v] > dp[s][u] + e[i].w){ dp[s][v] = dp[s][u] + e[i].w; if (!vis[v]) q.push(pii(dp[s][v], v)); } } } //第一种 最短路转移 rep (i,1,n){ for (auto x:V[i]){ int sta = 1<<(x.fi-1); int t = x.se; if (dp[s][i] <= t) dp[s|sta][i] = min(dp[s|sta][i], t); } } //第二种 原地转移 } void solve(int s, int dp[S][N], int *ans){ rep (i,0,(1<<K)-1){ ans[i] = inf; rep (j,1,n) dp[i][j] = inf; } dp[0][s] = 0; while (!q.empty()) q.pop(); rep (i,0,(1<<K)-1) trans(i, dp); //转移 rep (i,0,(1<<K)-1) rep (j,1,n) ans[i] = min(ans[i], dp[i][j]); rep (j,0,K-1) rep (i,0,(1<<K)-1) if (!((i>>j)&1)) ans[i] = min(ans[i], ans[i|(1<<j)]); // rep (i,0,(1<<K)-1) cerr<<ans[i] <<' '; // cerr<<endl; } void Main(){ scanf("%d%d%d", &n, &m, &K); cnt = 0; rep (i,1,n) head[i] = 0, V[i].clear(); rep (i,1,m){ int x, y, w; scanf("%d%d%d", &x, &y, &w); adde(x, y, w); adde(y, x, w); } scanf("%d%d", &E, &tmax); rep (i,1,E){ int p, x, t; scanf("%d%d%d", &p, &x, &t); V[x].push_back(pii(p, t)); } scanf("%d%d", &s1, &s2); solve(s1, dp1, ans1); solve(s2, dp2, ans2); ans = inf; rep (i,0,(1<<K)-1) ans = min(ans, max(ans1[i], ans2[((1<<K)-1)^i])); printf("%d\n", ans<=tmax?ans:-1); return; } int main(){ int T; scanf("%d", &T); while (T--) Main(); return 0; }
C. Magical Rearrangement
题意:告诉你一个数字里面有多少个 0 多少个 1 ... 多少个 9 ,让你构造出相邻数字不同并且没有前导零的字典序最小的数。无解输出 -1 。
做法:假设数总长为 n ,先特判单个 0 的情况,不要判成 -1 了。首先非零数字,如果有一个数字出现次数 $> \frac{n+1}{2}$ ,那么肯定无解;如果 0 出现次数 > $\frac{n}{2}$ ,那么也无解。其余肯定有解,考虑怎么构造。假设当前剩下长度为 len ,可以发现如果 len 为奇数,且如果有一个数字 d 出现次数 $= \frac{len+1}{2}$ ,那么必然是 d x d y d z d ... d 这样放置。所以当前位只能放 d 。其余情况都没有必须要放的数字,那么就找到最小的放上去就可以了。【吐槽:这题本来早就写好了...结果那个判单个 0 的那句话...写在了判 -1 的后面...我以为它判了 0 ...其实它判了 -1 ... 一直没找到错..我真的会栓q..】

#include<bits/stdc++.h> #define rep(i,x,y) for(int i=(x);i<=(y);i++) using namespace std; int n, a[100]; void Main(){ int mx = 0; n = 0; rep (i,0,9){ scanf("%d", &a[i]); mx = max(a[i], mx); n += a[i]; } if (n==1&&a[0]>0){puts("0"); return;} if (mx>(n+1)/2 || a[0]>n/2){puts("-1"); return;} int last=-1; rep (i,1,n){ int l = (n-i+1), st = i==1?1:0; if (l&1){ bool flag=0; rep (j,st,9) if (j!=last && a[j]==((l+1)/2)){ printf("%d", j); last=j; a[j]--; flag=1; break; } if (!flag){ rep (j,st,9) if (j!=last && a[j]){ printf("%d", j); last=j; a[j]--; break; } } } else{ rep (j,st,9) if (j!=last && a[j]){ printf("%d", j); last=j; a[j]--; break; } } } puts(""); return; } int main(){ int T; scanf("%d", &T); while (T--) Main(); return 0; }
D. Pattern Lock
题意:有一个 $n\times m$ 的点阵,现在你要把每个点用一笔画连起来(类似手机的图案密码),规定是相邻两个点之间的那条线上不能有别的点,以及相邻两条线要成锐角。构造方案。
做法:【真的好恶心啊这个构造题】应该有好多种方案,我说说我的(这个东西必须要画画才行)
首先如果 n 为偶数( m 为偶数是对应的),一定可以构造一种两行两行连的方案(如图)
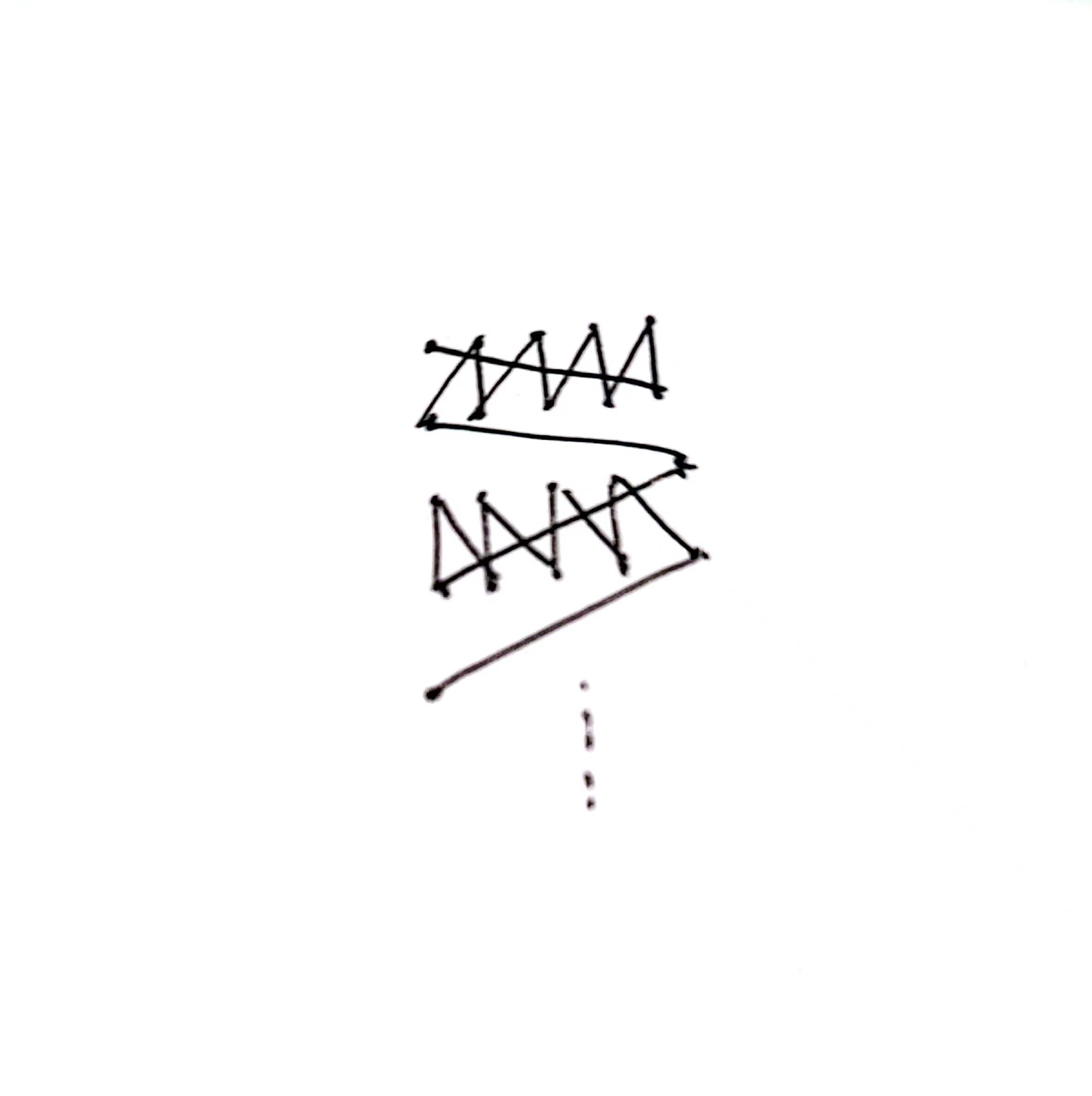
但是这个有个问题是如果 m = 2 ,n 为 偶数时,按照上面的方法处理有个角度是 90 度,所以要特判一下。
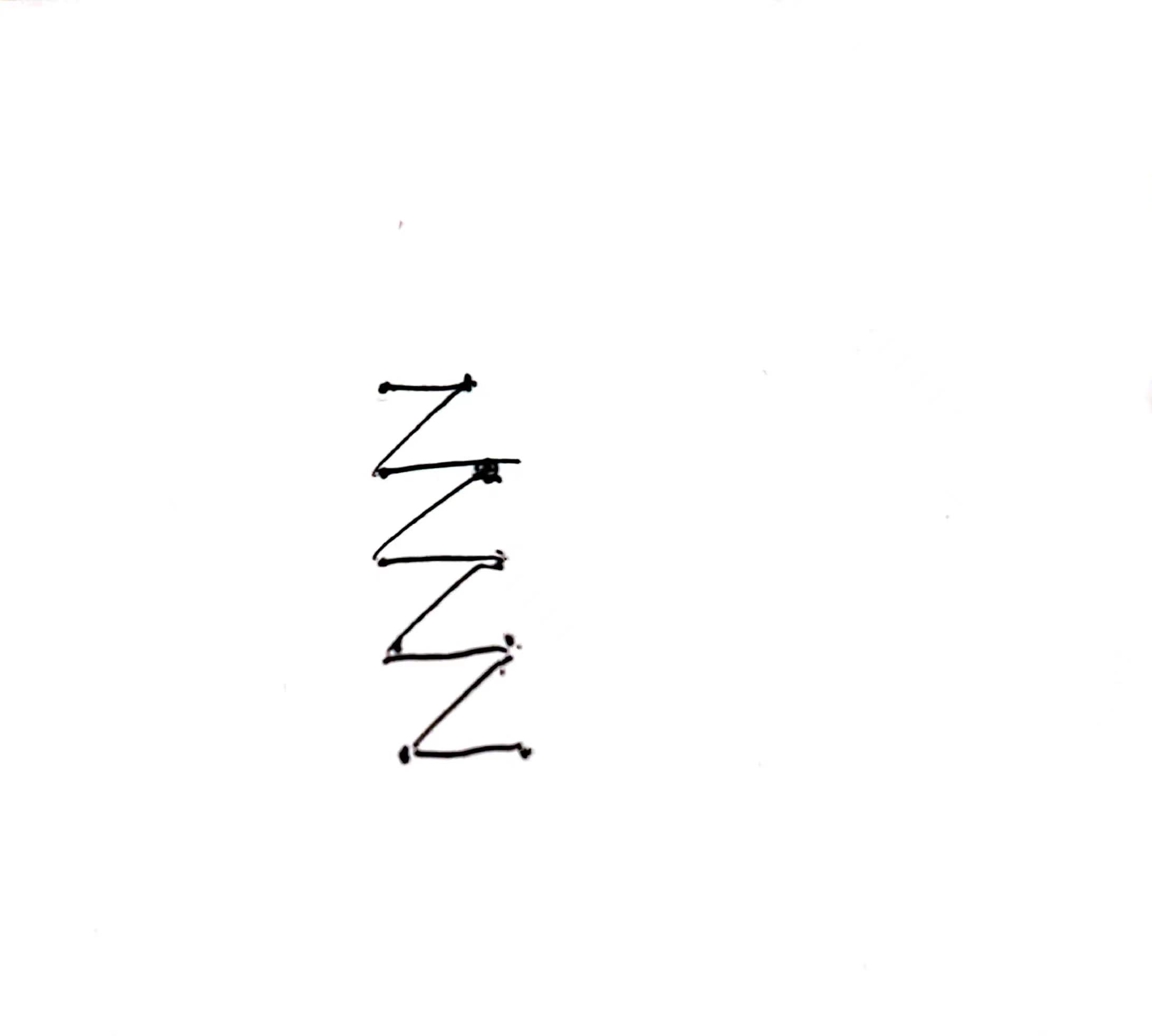
直接这样就好了。
然后看 n 和 m 都是奇数的情况,我是这样做的先按照偶数做到剩下三行,然后三行这么构造。
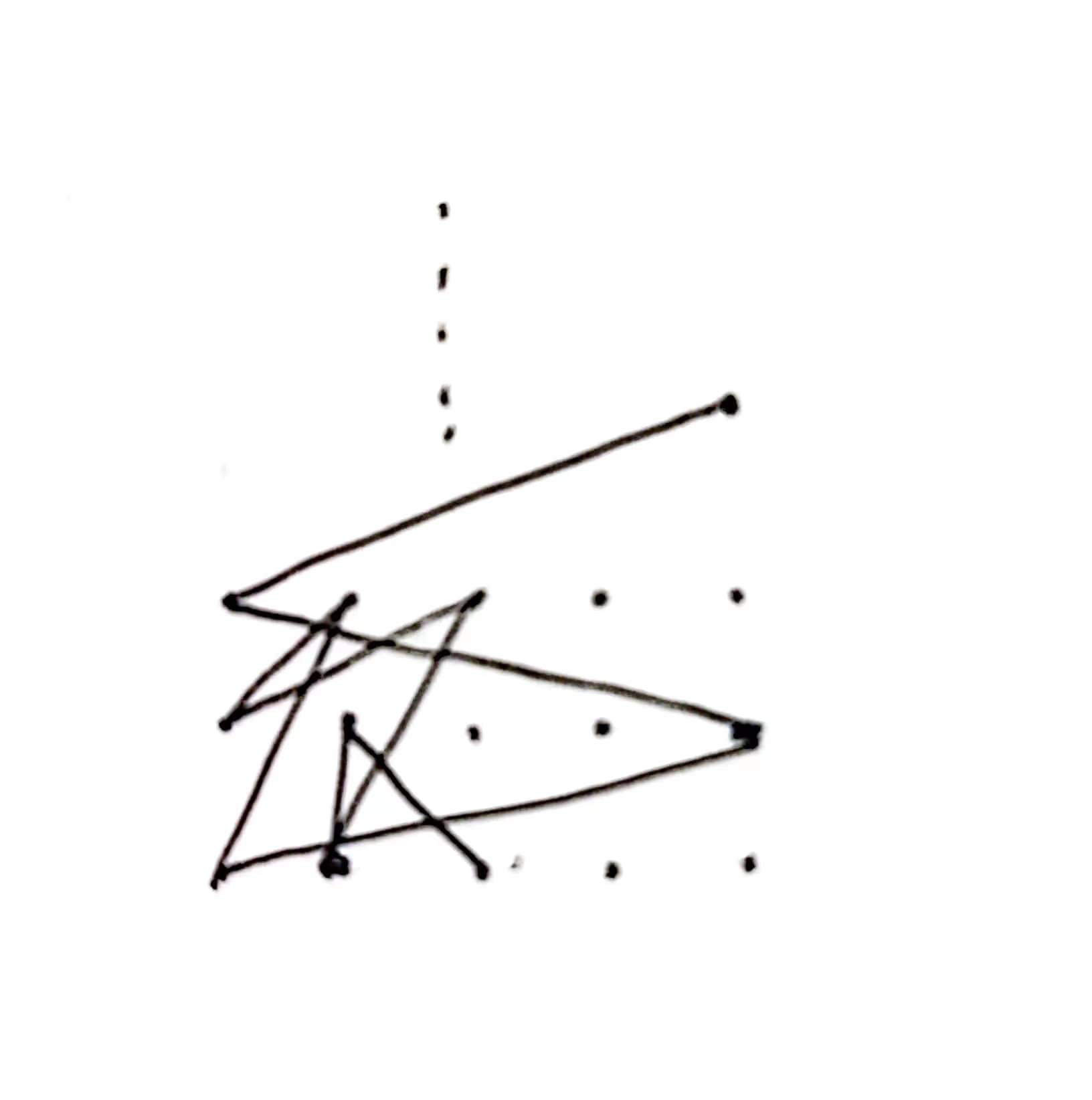
 .....依次下去。一定都是锐角。具体可以看代码。
.....依次下去。一定都是锐角。具体可以看代码。

#include<bits/stdc++.h> #define rep(i,x,y) for (int i=(x);i<=(y);i++) using namespace std; int n, m, now; int main(){ scanf("%d%d", &n, &m); if (n==1 && m==1){puts("1 1"); return 0;} if (n==2){ rep (j,1,m){ printf("%d %d\n", 1, j); printf("%d %d\n", 2, j); } return 0; } if (m==2){ rep (i,1,n){ printf("%d %d\n", i, 1); printf("%d %d\n", i, 2); } return 0; } if (!(n&1)){ now = 1; for (int i=1; i<=n; i+=2){ if (now==1){ printf("%d %d\n", i, 1); printf("%d %d\n", i+1, m); for (int j=m; j>=2; j--){ printf("%d %d\n", i, j); printf("%d %d\n", i+1, j-1); } now = 0; } else{ printf("%d %d\n", i, m); printf("%d %d\n", i+1, 1); rep (j,1,m-1){ printf("%d %d\n", i, j); printf("%d %d\n", i+1, j+1); } now = 1; } } return 0; } if (!(m&1)){ now = 1; for (int j=1; j<=m; j+=2){ if (now==1){ printf("%d %d\n", 1, j); printf("%d %d\n", n, j+1); for (int i=n; i>=2; i--){ printf("%d %d\n", i, j); printf("%d %d\n", i-1, j+1); } now = 0; } else{ printf("%d %d\n", n, j); printf("%d %d\n", 1, j+1); rep (i,1,n-1){ printf("%d %d\n", i, j); printf("%d %d\n", i+1, j+1); } now = 1; } } return 0; } now = 1; for (int i=1; i<n-2; i+=2){ if (now==1){ printf("%d %d\n", i, 1); printf("%d %d\n", i+1, m); for (int j=m; j>=2; j--){ printf("%d %d\n", i, j); printf("%d %d\n", i+1, j-1); } now = 0; } else{ printf("%d %d\n", i, m); printf("%d %d\n", i+1, 1); rep (j,1,m-1){ printf("%d %d\n", i, j); printf("%d %d\n", i+1, j+1); } now = 1; } } if (!now){ printf("%d %d\n", n-2, m); printf("%d %d\n", n-1, 1); printf("%d %d\n", n, m); for (int j=m; j>1; j-=2){ printf("%d %d\n", n-2, j-1); printf("%d %d\n", n-1, j); printf("%d %d\n", n-2, j-2); printf("%d %d\n", n, j-1); printf("%d %d\n", n-1, j-1); printf("%d %d\n", n, j-2); } } else{ printf("%d %d\n", n-2, 1); printf("%d %d\n", n-1, m); printf("%d %d\n", n, 1); for (int j=1; j<m; j+=2){ printf("%d %d\n", n-2, j+1); printf("%d %d\n", n-1, j); printf("%d %d\n", n-2, j+2); printf("%d %d\n", n, j+1); printf("%d %d\n", n-1, j+1); printf("%d %d\n", n, j+2); } } return 0; }
【这题解写的我好累】
【中间几题由于不可做所以没有放进训练赛里面..】
H. Reverse the String
题意:给一个字符串,你可以反转一个区间,问得到字典序最小的字符串是什么。
做法:【一开始想用 sa ..板子打好了以后发现不能这么做...】首先翻转的区间一定是左端点比右端点大,且左端点最靠前,根据这个可以确定左端点 L 。现在只需要找到右端点。首先右端点的字符一定是 L 之后最小的,可以把这些 R 都拿出来。然后我们依次反转来比较字典序。毕竟字典序的方法就是求 lcp 然后比较 lcp+1位置的大小。lcp 比较常见的是二分+hash以及后缀数组,但是这里面有反转,所以没法用 sa ,只能二分加 hash ,hash 维护一个正向一个反向。具体见代码。

#include<bits/stdc++.h> #define rep(i,x,y) for (int i=(x);i<=(y);i++) #define ll long long using namespace std; const int N = 1e5+10; const int bas = 10007; const int mod = 1e9+7; int n, m, h1[N], h2[N], pw[N], q[N], flag, L, R, tot, ans; char s[N], t[N]; set<int> S[500]; int get_h1(int l,int r){ return (h1[r] + mod - (ll)h1[l-1]*pw[r-l+1]%mod)%mod; } int get_h2(int l,int r){ l = m-l+1; r=m-r+1; swap(l, r); return (h2[r] + mod - (ll)h2[l-1]*pw[r-l+1]%mod)%mod; } int get_hash(int l,int p){ if (l<=p){ return get_h2(p-l+1, p); } else{ return ((ll)get_h2(1, p)*pw[l-p]%mod+get_h1(p+1, l))%mod; } } char get_pos(int pos,int p){ if (pos > p) return t[pos]; else return t[p-pos+1]; } bool cmp(int x, int y){ // cerr<<get_hash(3, 2)<<' '<<get_hash(3, 5)<<endl; int l=1, r=m, mid; while (l<=r){ mid = (l+r)>>1; if (get_hash(mid, x) == get_hash(mid, y)) l=mid+1; else r=mid-1; } int lcp = l-1; // cerr<<"lcp = "<<lcp<<endl; if (lcp == m) return 0; else return get_pos(lcp+1, x) < get_pos(lcp+1, y); } void Main(){ scanf("%s", s+1); n=strlen(s+1); rep (i,0,25) S[i].clear(); rep (i,1,n) S[s[i]-'a'].insert(i); tot = 0; L = 1, R = 1; tot=0; rep (i,1,n){ S[s[i]-'a'].erase(i); flag=0; rep (j,0,s[i]-'a'-1) if (!S[j].empty()){ for (auto x:S[j]) q[++tot] = x; flag = 1; break; } if (flag){L=i; break;} } if (!flag){ rep (i,1,n) printf("%c", s[i]); puts(""); return; } rep (i,1,L-1) printf("%c", s[i]); rep (i,L,n) t[i-L+1] = s[i]; m = n-L+1; rep (i,1,m) h1[i] = ((ll)h1[i-1]*bas + t[i])%mod; reverse(t+1, t+1+m); rep (i,1,m) h2[i] = ((ll)h2[i-1]*bas + t[i])%mod; reverse(t+1, t+1+m); // cerr<<cmp(5, 2)<<endl; ans = 1; rep (i,1,tot){ q[i] = q[i]-L+1; if (cmp(q[i], ans)) ans = q[i]; } reverse(t+1, t+1+ans); rep (i,1,m) printf("%c", t[i]); puts(""); return; } int main(){ pw[0] = 1; rep (i,1,N-1) pw[i] = (ll)pw[i-1]*bas%mod; int T; scanf("%d", &T); while (T--) Main(); return 0; }
I. Fake Walsh Transform
题意:有 $0, 1, 2, ... 2^m-1$ 这些数,给出一个 $< 2^m-1$ 的数 n ,问你最多可以用多少个数恰好异或出 n 。
做法:可以发现 $m > 1$ 时我们可以用 $0 .. 2^m-1$ 除掉 n 之外的数异或出 n ,肯定是最多的了,而 $n=0$ 时甚至不用除掉 n 。 $m = 1$ 要特判,$n=0$ 时要除掉 1 ,$n =1$ 时反而可以全选上。

#include<bits/stdc++.h> #define rep(i,x,y) for (int i=(x);i<=(y);i++) #define ll long long using namespace std; ll n, m; void Main(){ scanf("%lld%lld", &m, &n); if (m==1){ if (n==0) puts("1"); else puts("2"); return; } if (!n) cout<<(1ll<<m)<<endl; else cout<<(1ll<<m)-1<<endl; return; } int main(){ int T; scanf("%d", &T); while (T--) Main(); return 0; }
J. Anti-merge
题意:给一个矩阵,每个格子里面有数字,相邻如果是相同数字可以合并。现在你可以给他们打上 tag ,使得只有相同数字相同 tag 才可以合并。你要使得所有格子都没法合并,问你最少用多少种颜色的 tag ,以及这种条件下,最少要给多少个格子打 tag 。
做法:不难发现,颜色最少只要一种肯定够了。对于同一个数字的连通块,一种颜色的话说明打 tag 都不能相邻,然后你给这个棋盘黑白染色,相当于要么全给白格子打 tag ,要么全黑,就看那种颜色格子数最少就好了。

#include<bits/stdc++.h> #define rep(i,x,y) for (int i=(x);i<=(y);i++) #define pii pair<int,int> #define fi first #define se second using namespace std; const int N = 505; const int dx[4]={0,0,1,-1}; const int dy[4]={1,-1,0,0}; int n, m, vis[N][N], cnt0, cnt1, tot, a[N][N]; pii Q[N*N]; vector<pii> ans; bool chk(int x,int y){ return (1<=x&&x<=n) && (1<=y&&y<=m); } void dfs(int x,int y){ // cerr<<x<<' '<<y<<endl; Q[++tot] = pii(x,y); vis[x][y]=1; if ((x+y)&1) cnt1++; else cnt0++; rep (i,0,3){ int tx = x+dx[i], ty = y+dy[i]; if (chk(tx, ty) && a[tx][ty] == a[x][y] && !vis[tx][ty]) dfs(tx, ty); } } int main(){ scanf("%d%d", &n, &m); rep (i,1,n) rep (j,1,m) scanf("%d", &a[i][j]); rep (i,1,n) rep (j,1,m) if (!vis[i][j]){ cnt0 = cnt1 = tot = 0; dfs(i,j); int op; if (cnt0<cnt1) op=0; else op=1; rep (k,1,tot) if (((Q[k].fi+Q[k].se)&1) == op) ans.push_back(Q[k]); } if ((int)ans.size()==0) puts("0 0"); else{ printf("1 %d\n", (int)ans.size()); for (auto x:ans) printf("%d %d 1\n", x.fi, x.se); } return 0; }
K. Longest Continuous 1
题意:有一个 s 串是0, 1, 2, 3... 的二进制拼起来的。然后现在问 s 串长为 k 的前缀里面最长连续的 1 有几个。
做法:找规律就好了。大概就是在每次 2 的幂次的位置答案会加一。

#include<bits/stdc++.h> #define rep(i,x,y) for(int i=(x);i<=(y);i++) #define ll long long using namespace std; int n; void Main(){ scanf("%d", &n); if (n==1){puts("0"); return;} else if (n==2){puts("1"); return;} ll x = 1, now = 2, i = 1; while (now<n){ x = x*2ll; i ++; now = now+x*i; } printf("%lld\n", i); return; } int main(){ int T; scanf("%d", &T); while (T--) Main(); return 0; }
L. Tree Game
题意:有一棵树,有一些节点的数字已知,剩下的未知,你要把他们补全,补成一个排列。然后补完之后,你可以每次操作一个非叶节点,你可以把该节点和它的儿子上的值重新排列,问你可以把它排成任意 i 号节点的值为 $a_i$ 的方案数。
做法:对于最下面的叶节点和它的父亲来考虑,可以发现如果已知的数字中,出现了两个及以上叶节点编号以外的值,那么就无解。否则的话,如果有一个以外的值,这个值就应该放在父亲上;否则父亲的值暂时未知。我们统计这个父亲和儿子中 $a_i$ 为 0 的节点个数 cnt0 ,如果如果有一个以外的值,方案数就应该乘上 $cnt0!$ ,并且把这个值赋给父亲,否则,父亲的值未知,相当于父亲的值暂时为 0 ,方案数乘上 $(cnt0-1)!$ 。然后我们再接着向上统计。最后 $a_1$ 的值必须是 1 或者 0 不能是其他数。

#include<bits/stdc++.h> #define rep(i,x,y) for (int i=(x);i<=(y);i++) #define ll long long using namespace std; const int N = 2e5+10; const int mod = 998244353; int n, a[N], cnt, head[N], vis[N], fac[N], ans, flag; struct edge{ int to, nxt; }e[N]; void adde(int x,int y){ e[++cnt].to=y; e[cnt].nxt=head[x]; head[x]=cnt; } void dfs(int u){ if (!flag) return; for (int i=head[u]; i; i=e[i].nxt) dfs(e[i].to); if (!head[u]) return; for (int i=head[u]; i; i=e[i].nxt) vis[e[i].to] = 1; int cnt=0, cnt0=0; if (a[u] && !vis[a[u]]) cnt++; if (!a[u]) cnt0++; for (int i=head[u]; i; i=e[i].nxt){ int v = e[i].to; if (a[v]!=0){ if (!vis[a[v]]) cnt++; } else cnt0++; } if (cnt>1){flag=0; return;} if (cnt == 1){ ans = (ll)ans*fac[cnt0]%mod; for (int i=head[u]; i; i=e[i].nxt){ int v = e[i].to; if (a[v]&&!vis[a[v]]){a[u] = a[v]; break;} } if (a[u]&&!vis[a[u]]) a[u]=a[u]; } else if (cnt0){ a[u] = 0; ans = (ll)ans*fac[cnt0-1]%mod*cnt0%mod; } for (int i=head[u]; i; i=e[i].nxt) vis[e[i].to] = 0; } void Main(){ scanf("%d", &n); cnt = 0; rep (i,1,n) head[i] = vis[i]=0; rep (i,2,n){ int x; scanf("%d", &x); adde(x, i); } rep (i,1,n) scanf("%d", &a[i]); flag=1; ans = 1; dfs(1); if (a[1]&&a[1]!=1) puts("0"); else{ if (!flag) puts("0"); else printf("%d\n", ans); } return; } int main(){ fac[0]=1; rep (i,1,N-1) fac[i]=(ll)fac[i-1]*i%mod; int T; scanf("%d", &T); while (T--) Main(); return 0; }
【写完题解啦好有成就感 yeahyeah





