DS博客作业05--查找
0.PTA得分截图

1.本周学习总结
什么是ASL
- 关键字的平均比较次数,也称平均搜索长度
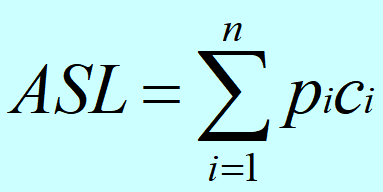
顺序查找(长度为n)
- 成功ASL
- 有序表:(n+1)/2
- 无序表:(n+1)/2
- 不成功ASL
- 有序表:n/2+n/(n+1)
- 无序表:n+1
二分查找(以二叉树为例)
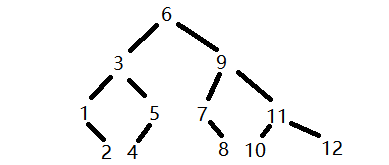
- 成功ASL
- (1+22+34+4*4)/12=3.08
- 不成功ASL
- (33+410)/13=3.77
二叉搜索树
- 性质:任意结点的左孩子的键值小于该结点,右节点大于该结点;中序遍历序列为升序序列
- 结构体
typedef struct TNode
{
int Data;
struct TNode* Left;
struct TNode* Right;
}BSTNode, *BSTree;
- 建树、插入代码
BSTree CreateTree(BSTree T, int x)
{
if (!T)
{
T = new BSTNode;
T->Data = x;
T->Left = T->Right = NULL;
}
else
{
if (x < T->Data)
{
T->Left = CreateTree(T->Left, x);
}
else if (x > T->Data)
{
T->Right = CreateTree(T->Right, x);
}
}
return T;
}
- 删除代码
BinTree Delete( BinTree BST, ElementType X )
{
Position Tmp;
if(!BST)
printf("Not Found\n");
else
{
if(X<BST->Data)
BST->Left=Delete(BST->Left,X);
else if(X>BST->Data)
BST->Right=Delete(BST->Right,X);
else
{
if(BST->Left&&BST->Right)
{
Tmp=FindMin(BST->Right);
BST->Data=Tmp->Data;
BST->Right=Delete(BST->Right,BST->Data);
}
else
{
Tmp=BST;
if(!BST->Left)
BST=BST->Right;
else
BST=BST->Left;
free(Tmp);
}
}
}
return BST;
}
AVL树(平衡二叉树)的定义及四种调整做法
- 定义:树中每个结点的左、右子树深度之差(称为平衡因子BF)只能取:-1、0、1
- 例:
- 平衡二叉树
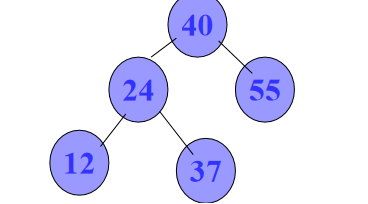
- 非平衡二叉树

- 平衡二叉树
- 四种旋转
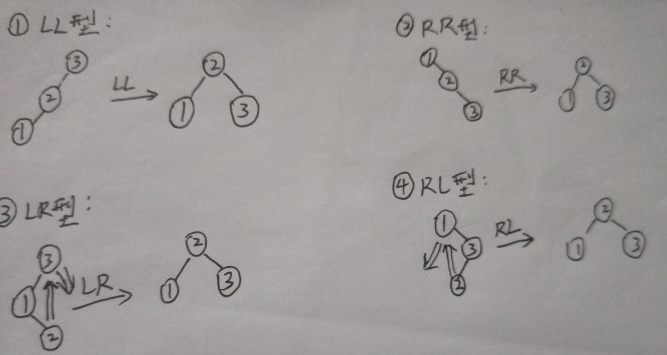
B-树和B+树的定义
- B-树定义
一棵m阶B-树或者是一棵空树,或者是满足下列要求的m叉树
每个节点至多m个孩子节点(至多有m-1个关键字)
除根节点外,其他节点至少有m/2(取上界)个孩子节点(即至少有m/2(取上界)-1个关键字); - B+树定义
一棵m阶B+树满足下列条件:
1.每个分支节点至多有m棵子树。
2.根节点或者没有子树,或者至少有两棵子树
3.除根节点,其他每个分支节点至少有m/2(取上界)棵子树
4.有n棵子树的节点有n个关键字
B-树的插入、删除操作
- 插入
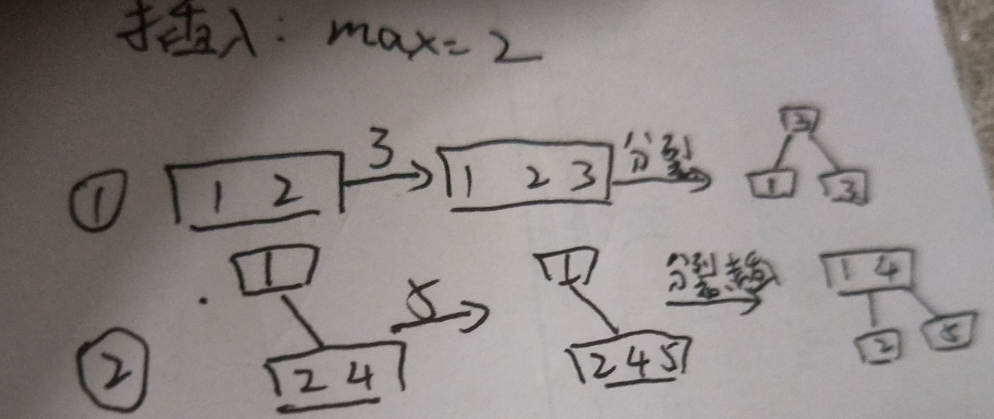
- 删除
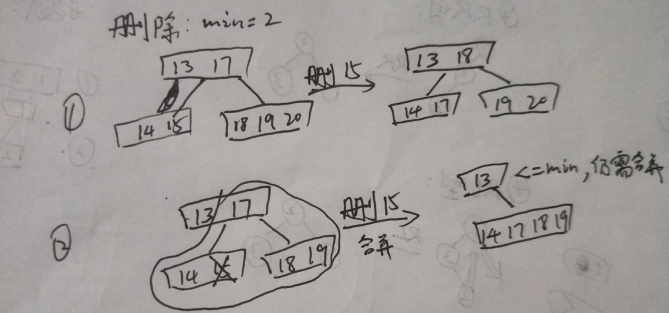
- 删除的操作比插入更容易理解错误,需要多花时间理解
哈希表
2.PTA题目介绍
2.1 7-1 是否完全二叉搜索树 (30分)
2.1.1该题的设计思路
-
思路
本题算是复习之前的知识点加上完全二叉树的应用,根据完全二叉树的定义,任何一个结点有右孩子没有左孩子为false,同时有左孩子没有右孩子的情况最多出现一次,其右侧不能有任何非叶子结点,因此我用的层次遍历实现,代码用flag标记次数
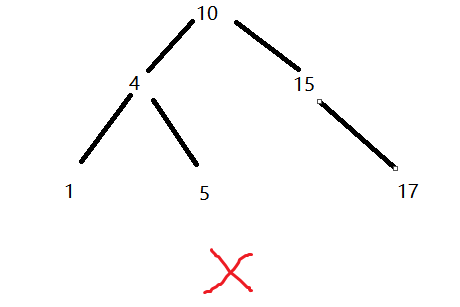
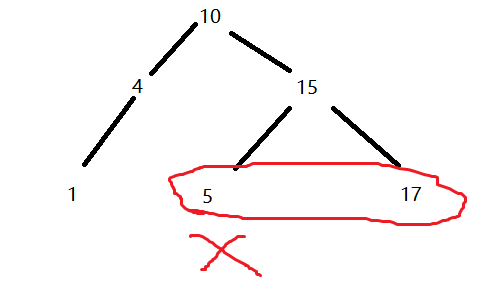
-
时间复杂度O(N)
2.1.2该题的伪代码
- 伪代码(仅介绍关键代码main+IsCompleteBTree函数)
int main()
{
定义数据长度N,树tree;
初始化tree;
输入N;
for i=0 to N-1
输入N个数据插入tree中建树;
end for
调用函数Levelorder用于层次遍历并输出
调用函数IsCompleteBTree判断是否是完全二叉树
}
bool IsCompleteBTree(BinTree T)
{
建队列;
建一个树的指针temp=T;
定义flag//当第一个叶子结点或者第一个有左孩子没有右孩子的结点出现时flag+1;
temp进队;
while(队列不空)
if(temp有右孩子没有左孩子)返回否false;
else if(temp有左孩子没有右孩子)flag+1,左孩子进队;
else if (temp有左右孩子)
if(之前出现过有左孩子没有右孩子的结点,即flag>=1)返回否false;
else 左右孩子进队;
else
if(第一次出现叶子结点)flag+1;
if(flag>1)即错误俩次,返回否false;
temp=队首结点;//temp依次为层次遍历的每个结点
end while
出循环返回正确true;
}
- 具体代码截图





2.1.3提交列表说明

- 错误1:最大N-1,NO,无度1结点。此处错误大致猜测为某个结点无左右孩子,其下一个结点有左右孩子
- 答案正确:新增一个判断,当某个结点无左右孩子时,再出现其他结点有孩子则返回false
2.1.4本题设计的知识点
- 考察对完全二叉树的理解
- 考察层次遍历
2.2 7-2 二叉搜索树的最近公共祖先 (30分)
2.2.1该题的设计思路
- 思路
通过俩个数与当前结点的不断比较最终确定祖先的位置,思路不难,难在运行速度,如果树的形状比较奇怪,可能会超时过不了,就需要进行调整 - 时间复杂度O(n)
2.2.2该题的伪代码
- 伪代码(只讲核心代码main+Find函数)
int main()
{
输入待查询结点对数和结点个数M,N;
for
先序序列输入N个数并建树;
end for
for
输入M对结点数;
用bool1保存查询第一个数是否在树内的结果,bool2保存另一个数的结果;
当bool1和bool2不都为true时,依据情况输出哪个数找不到或者都找不到;
当都为true时,用result保存调用Find函数找公共祖先的结果;
if(result为俩个数据的其中一个)输出 该数据为另一个数据的祖先;
else result为其他数据,则该数据为输入的俩个数的祖先;
end for
}
int Find(BinTree T, int a, int b)
{
while(T不空)
if(a和b都小于T的键值)T=T的左孩子;
else if(a和b都大于T的键值)T=T的右孩子;
else a和b一个在左一个在右,或者有=T的键值的情况,那么T就是它们的祖先或者是其中一个是另一个祖先,返回T的键值;
end while
}
- 具体代码截图
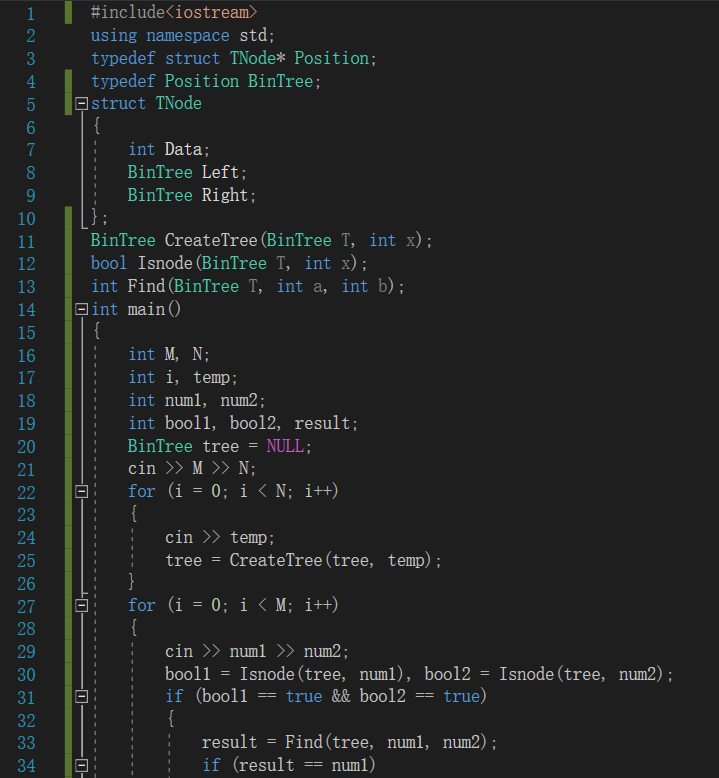
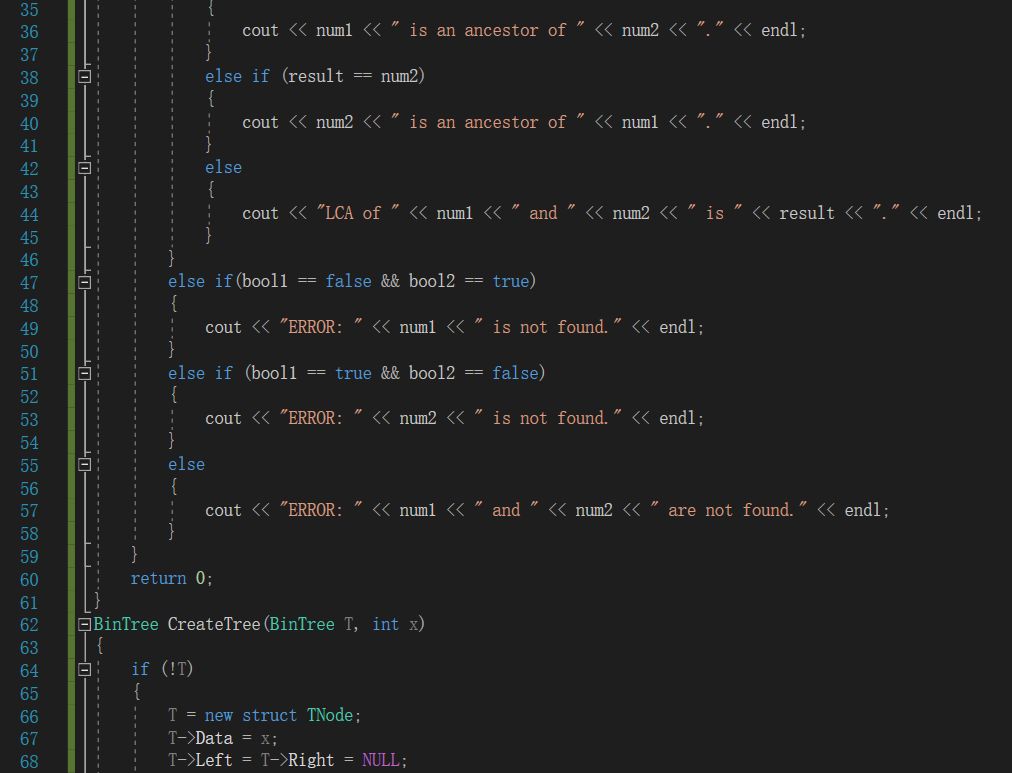
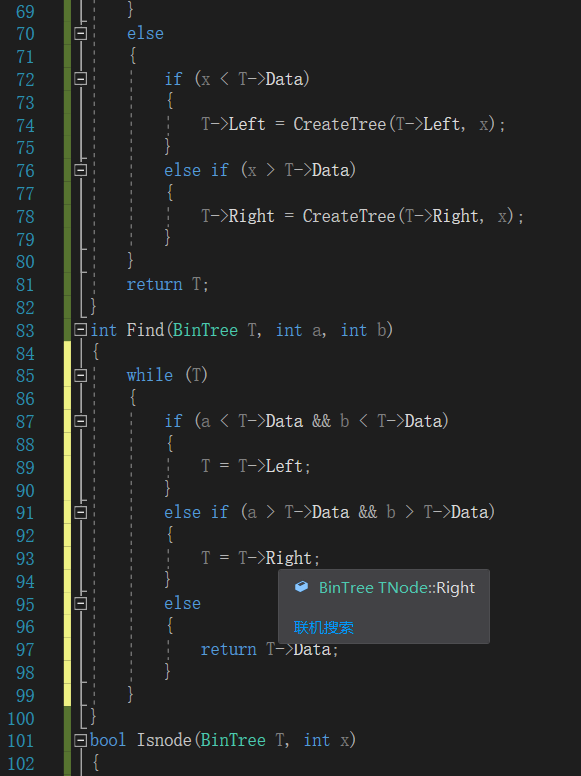
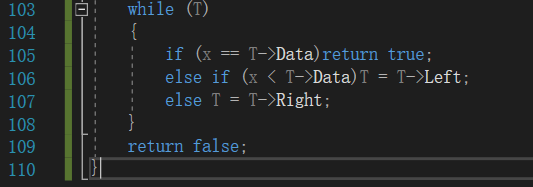
2.2.3提交列表说明
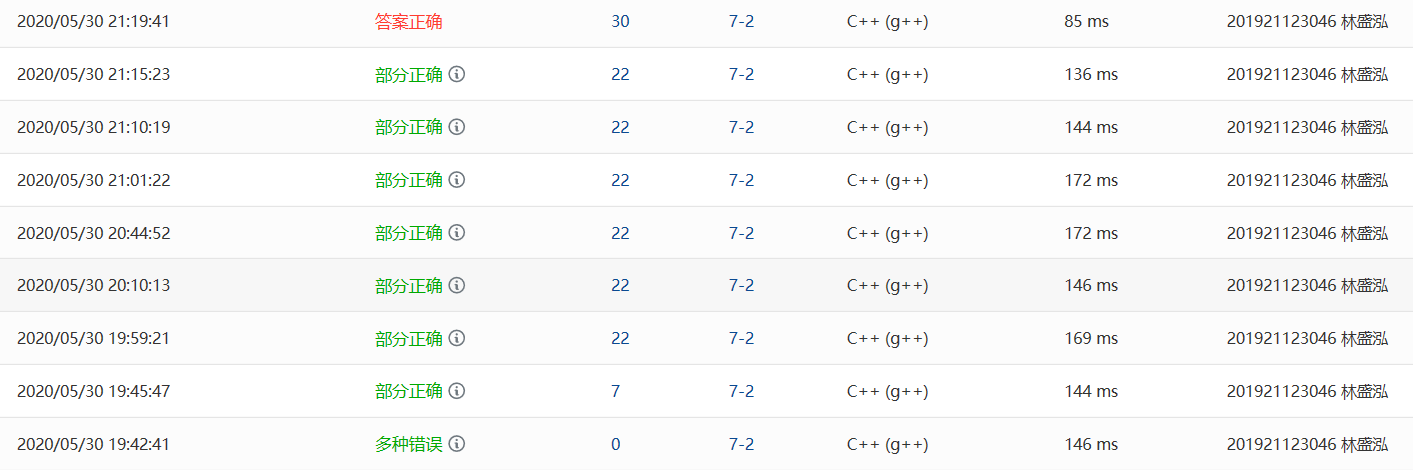
- 错误1:漏掉格式中的"."
- 错误2:没有判断U=V的情况,测试点1,4错误
- 错误3:运行超时,经过不断尝试优化代码,最终通过测试点
2.2.4本题设计的知识点
- 二叉搜索树的灵活运用,可以根据大小,省去递归遍历另一子树的过程
- 仅知道先序遍历就可建二叉搜索树
2.3
急速加工ing





