DS博客作业04--图
0.PTA得分截图

1.本周学习总结(0-5分)
1.1 总结图内容
- 图存储结构
//邻接矩阵
#define MAXV //决定数组大小
typedef struct
{
int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数,弧数
} MGraph;
//邻接表
typedef struct ANode
{
int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表
typedef struct Vnode
{
int data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef struct
{
VNode adjvex[MAXSIZE]; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
- 建图
//建邻接矩阵
void CreateMGraph(MGraph& g, int n, int e)//建无向图
{
int i, x, y;
int vex1, vex2;
g.n = n, g.e = e;
for (x = 0; x < n; x++)
{
for (y = 0; y < n; y++)
{
g.edges[x][y] = 0;
}
}
for (i = 0; i < e; i++)
{
cin >> vex1 >> vex2;
g.edges[vex1 - 1][vex2 - 1] = 1;
//有向图写到这为止
g.edges[vex2 - 1][vex1 - 1] = 1;
}
}
//建邻接表
void CreateAdj(AdjGraph*& G, int n, int e) //创建图邻接表
{
int i;
int a, b;
ArcNode* p1, * p2;//有向图去掉p2
G = new AdjGraph;
G->n = n, G->e = e;
for (i = 1; i <= n; i++)G->adjlist[i].firstarc = NULL;
for (i = 0; i < e; i++)
{
p1 = new ArcNode;
p2 = new ArcNode;//有向图去掉这句
cin >> a >> b;
p1->adjvex = b;
p1->nextarc = G->adjlist[a].firstarc;
G->adjlist[a].firstarc = p1;
//有向图写到这里
p2->adjvex = a;
p2->nextarc = G->adjlist[b].firstarc;
G->adjlist[b].firstarc = p2;
}
}
- 图遍历及应用
//深度优先搜索DFS
void DFS(AdjGraph* G, int v)
{
ArcNode* p;
visited[v] = 1;
p = G->adjlist[v].firstarc;
while (p)
{
if (visited[p->adjvex] == 0)
{
DFS(G, p->adjvex);
}
p = p->nextarc;
}
}
//广度优先搜索BFS
void BFS1(AdjGraph* G, int v)//连通图
{
queue<ArcNode*>q;
ArcNode* p;
visited[v] = 1;
q.push(G->adjlist[v].firstarc);
while (!q.empty())
{
p = q.front();
while (p)
{
if (visited[p->adjvex] == 0)
{
visited[p->adjvex] = 1;
q.push(G->adjlist[p->adjvex].firstarc);
}
p = p->nextarc;
}
q.pop();
}
}
void BFS2(AdjGraph *G)
{ int i;
for (i=0;i<G->n;i++)
if (visited[i]==0)//不重复遍历已遍历的顶点
BFS1(G,i);
}
- 判断图是否连通
- 使用BFS1或DFS遍历一遍后,visited数组都为1即图为连通
- 最短路径
//Dijkstra算法
- 最小生成树相关算法及应用
//Prim算法
//Kruskal算法
- 拓扑排序
- 关键路径
1.2.谈谈你对图的认识及学习体会。
学完非线性结构中最实用的图,或许有了树的基础,学起来不会太蒙,但在写代码的时候真的挺难,很多地方写起来不像学起来一样直白,有时候连自己想的思路写起来的磕磕碰碰的,可能还需要花一段时间才能熟练掌握
2.阅读代码
2.1 题目及解题代码
-
题目
-
解题代码

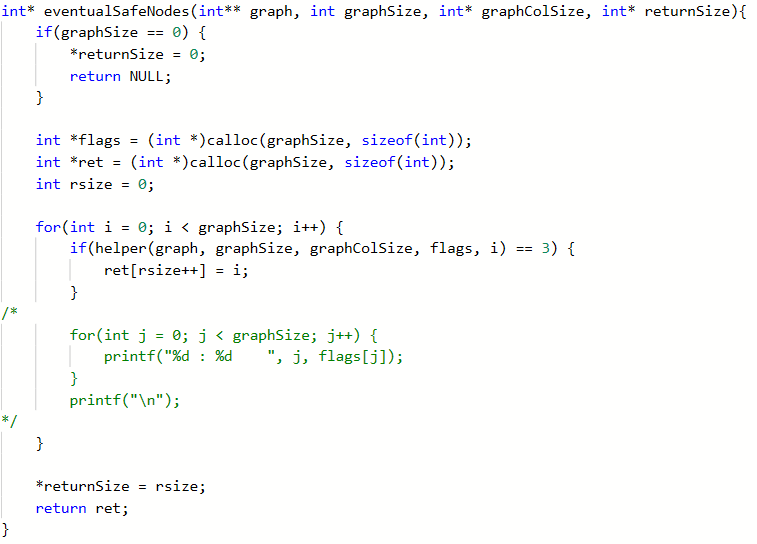
2.1.1 该题的设计思路
本体利用DFS+道标完成,首先设置一个路标数组,0-3分别代表四种状态,未访问,已访问,非安全,安全,通过DFS遍历每个结点,对每个结点的下个结点遍历失败,本节点失败,若不失败则返回成功
2.1.2 该题的伪代码
2.1.3 运行结果
网上题解给的答案不一定能跑,请把代码复制自己运行完成,并截图。





